例谈基于“儿童视角”的小学数学例题教学

于正军

随着新课程改革的逐步推进和不断深化，新一轮课程改革的理念和精神更加符合社会发展，更加顺应学生的成长，也更加被教育所认可，从而对进入“后课标时代”的教材、教师及教学提出了更高要求，即在平时的教学实践中，教师在深度把握教材的基础上如何设计出顺应学生发展的课堂教学。笔者以为常态的课堂理应开展“儿童视角”的例题教学，在自主运用教材的过程中促进儿童的思维持续不断地发展。

一、 从例题标注走向儿童思疑

为了能更加接近儿童，增强教材的活泼性、人文性及趣味性，新教材在例题的重、难点处以形式活泼的标注提醒和强化此例题在教学过程中的关键点，以便有针对性地为教师备课和学生学习突出重点、突破难点指明方向。可是在教学实践过程中，很多教师机械地把例题中的标注提示语作为例题教学的唯一重点进行教学，不关注学生在学习过程中的思维疑点，忽略了学生在学习过程中所表现出来的思维的现实状况和个性差异。

如，教学“三位数除以一位数”。

通过多次教学实践发现，其实这条提示语并不能反映本例题教学的难点。课堂上，当学生尝试练习或巩固练习时，没有人把“4”不写在“9”的上面。究其原因，一方面是学生在二年级已经初步掌握除法竖式的书写形式，学生会这样按部就班地写。另一方面，本例题被除数每个数位上的数均能除以“2”，不存在前一位不够除要看后两位，从而引发学生讨论商应写在哪一位上的问题。因此，从这个意义上说，这一提示语未能关注儿童的认知“缺口”，即学生（特别是学困生）出错的地方不在于此，而是在计算过程中“移”数不会移。如例题中，当百位上除完后，要把被除数十位上的8移下来，学生不知道怎么“移”数，特别是学困生，要么不知道8移下来是写在1的左边还是右边，要么就错误地把8和6一块儿移下来。这足以说明学生对于每一步计算的算理全然不知，未能体会到每一步是表示“几个几除以2”这一“包含除”的除法原理。

针对学生不会“移”数的现象，教师教学时不能把本例题教学的难点机械地聚焦在“4为什么写在商的百位上”这一知识点上，理应基于学生的思维疑点引导学生展开“儿童视角”的算理探索：第一，百位上的9除以2得到的4表示什么？（4个百）所以这里的4应该写在商的哪一位上？第二，9个百除以2得到4个百还余1个什么？（1个百）1个百除以2不够除了咱们就怎么样呢？（生：把8移下来）8表示什么呢？（8个十）那1个百和8个十合起来是……？（18个十），所以8移下来应该写在1的左边还是右边？18个十除以2得到9个什么？（9个十）9应该写在商的哪一位上？……如此引导学生经历除法算理的探索过程，学生不仅知道每一次除得的商应写在哪一位上，也深刻体会到了每一次只能移一个数，并知道移下来的数所写的位置。这样就能有效地避免学生在后续的学习中遇到不够商1，一下子移下两个数而忘记商0的情况。

因此，教师教学时不能套用教材中的提示语直接试问，而要根据学生的学习现实，灵活调整并拓展标注提示语的内涵及核心。本例题提示语可以拓展为：“这里的4表示什么？应该写在商的哪一位上？接下来的商为什么写在商的十位上？”如此教学，学生不仅能在亲历算理的过程中自然建构计算的方法，亦能对后续的除法计算算理的理解和方法的形成打下坚实的思维基础。

二、 从例题方法走向儿童思路

新教材中的例题所呈现出来的解题方法和步骤是遵循普遍性、一般性的学习规律的，更是一种规范的学习方法。但是，由于教材中的学习方法经过编写人员的提炼、概括这一“成人化”的过程后，或多或少地浸润了一些成人的思维因素。从这个意义上说，教材中所呈现的学习方法，不完全是适合所有儿童理解与接收的方法，不一定符合学生思维过程中的最佳路径，因为儿童的思维是有差异性的。所以一线教师在教学时，要从“儿童视角”设计教学，要善于解读学生内心深处的想法，而不是一味地机械“传输”教材中的方法。

例如，教学“图形覆盖中的规律”。教师出示： 3 4 5 6 7 8 9 10 11 12 13，可以框出几个不同的和？学生经过思考后交流：13-1=12（种）。教师纠正学生的回答并引导：每次框几个数？一共可以平移几次？继而让学生说出：13-2+1的算式。细细分析学生说出的算式：13-1=12是有自己想法的，这里面是有规律可循的，教师在课堂上没有必要硬拉着学生顺着教材的方法去引导。因为每次平移总是一格一格地往右边平移。所以，不管框里框几个数，只要把框里的最后一个数看作第一次平移过的数，这样从总个数里减去框里除了最后一个数以外的数的个数即能得到答案。如，       框里有两个数，就减去前面一个数（圈里的数）——13-1=12，框里有三个数就减去前面两个数（圈里的数）——13-2=11，框里有四个数就减去前面三个数（圈里的数）——13-3=10，以此类推。这样，学生解决此类问题只要一步计算的算式就能得出不同和的个数，而不需要列出两步计算的算式：13-2+1=12、13-3+1=11、13-4+1=10。在实际教学中，相当一部分学生特别是后进生，一开始根本不理解为什么要加1？而且在解题过程中，又经常把“+1”这一步遗忘，造成解题错误。所以教师在课堂上要善于研读教材，解读学生内心深处的想法，让学生的思维深度与广度在教材方法和成人思维的联接点上得以有效延伸。如此从“儿童视角”出发设计教学，才能真正实现创造性地使用教材，发挥教材的最大功能，彰显教材的最大价值。

三、 从例题图示走向儿童思考

新教材中的例题图示，一方面能直观地呈现例题所要表达的意图，促进学生直观形象的理解;另一方面能引导学生通过读图，不断增强学生识图、用图的意识，促进学生几何直观能力的逐步提高。但是在平时的教学实践中，部分教师过多地依赖例题中的图示进行教学，对学生学习效果的评价也置于例题图示的情境模式之中，从而忽略了学生对例题学习的真实理解。因此例题教学有时需要跳出图示模式学数学。

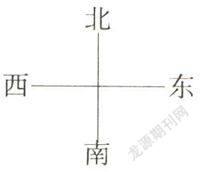
例如，教学“确定位置”，一旦教师引出方向图：

学生面对这个“十”字图示时，能够很快说出“北偏东、北偏西、南偏东、南偏西”这四个方向，而学生离开这个“十”字图示时，却很难快速说出这四个方向。所以教师教学时，在结合“十”字方向图引导学生认识方向后，有必要把“十字”隐去，引导学生讨论：现在你还能说出方向吗？你发现了什么？有什么技巧吗？只有这样引导学生去深度思考，才会把已有的“东南、东北、西南、西北”等知识经验有效迁移到“北偏东、北偏西、南偏东、南偏西”的方位内涵中，从而真正掌握方向、理解概念。因此，数学教学只有从“儿童视角”出发，不断关注儿童思维，让学生置身于“模式”之外进行学习，教师跳出“框架”对学生进行学习效果的评价，才能触摸学生思维深处的想法，继而促进高效教学目标的真正达成。

四、 从例题表述走向儿童思维

在例题教学中，每每需要表达一些较为抽象的数学概念或数学定义时，教材一般都是在呈现例题情境后直接给予表述，而如此的表述学生往往无法直接感悟知识的“来龙去脉”。所以，一线教师在教学时不能机械地把例题中的概念表述直接抛给学生，否则学生不但不理解知识内涵，也无法接受这一知识“规定”，对后续的学习会形成思维障碍。课堂上，教师要从例题表述出发，关注学生思维，让学生经历概念表述的形成过程，促进其对知识的领悟和内化。

例如，教学“认识比”。教材中表述：速度=路程÷时间，也可以用比来表示路程和时间的关系。接着呈现“两个数的比可以表示什么？”在此基础上引导学生说出两个数的比表示两个数相除。在教学实践中，当教师提出“两个数的比可以表示什么？”时，没有学生回答“两个数的比表示两个数相除”之类的话语。课堂上学生出现这一情况，说明教师在教学时，未能从例题表述走向儿童思维，而是直接把例题表述灌输给学生。究其原因，学生此时在课堂上会呈现出如下思维：教材上说也可以用比来表示路程和时间的关系，照这样的意思，当然也可以用比表示路程和速度之间的关系，为什么不可以用比来表示速度和时间的关系呢？所以学生在学习过程中，不因为教材中把“速度=路程÷时间”这个除法数量关系式呈现出来，学生就能想到两个数的比就表示两个数相除。故而，教师教学时，要从学生思维的角度出发，把同类量的比和不同类量的比结合起来引导学生领悟这一数学结论。要让学生感悟到“两个数的比可以表示两个数相除”，不是只有不同类量的比才可以表示两个数相除，同类量的比更加能够表示两个数相除的含义。

课堂上可作如下实践：当教师提问：可以怎样表示牛奶与果汁的杯数这两个数量之间的关系后，学生说出：果汁的杯数相当于牛奶的 ，牛奶的杯数相当于果汁的时 ，教师顺势引出：这两个数量之间的关系还可以说成：果汁与牛奶杯数的比是2比3，牛奶与果汁杯数的比是3比2。此时教师应有意引导学生观察比较这两组数量关系式，促进学生初步感知：果汁与牛奶杯数的比是2比3，就表示果汁的杯数相当于牛奶的 ，牛奶与果汁杯数的比是3比2，就表示牛奶的杯数相当于果汁的 ，进而引领学生进一步感知：2比3就是 ，3比2就是 。

如此引领学生思维，学生就很自然地把比的意义与分数及除法联系起来，从而促进学生对比的意义的自然建构，教师只有引导学生在同类量比的意义感知的基础上，再次引导学生探索不同类量比的含义，学生才会真正领悟“两个数的比可以表示两个数相除”这一比的意义。所以，在引导学生理解抽象的数学概念的意义时，教师要从“儿童视角”出发，排除学生思维上的障碍，促进学生积极思维，继而经历数学结论的形成过程，这样学生才会接受并认可教材中的例题表述，并达到深刻理解。【责任编辑：陈国庆】