教师深度引领学生自主建构*

☉江苏省丹阳市第五中学蒋伟

教师深度引领学生自主建构*

☉江苏省丹阳市第五中学蒋伟

学生的学习以接受与探究两种认识方式相辅相成，即借助语言获得知识的接受方式与指导学生操作与思考获得知识的探究式学习·这两种基本形态有机结合才能形成合理的教学认知活动·教师通过深度研究教学内容，提出恰当精准的问题，引导学生思考，进而解决问题，能使学生的学习欲望得到激发，学习潜力得到拓展，真正实现学生对知识的自主建构·

一、通过寻疑—质疑—析疑，引导学生科学建构

教师以学生学习过程中产生的问题为诱因创造问题情境，揭示学生认识上的矛盾，一方面可以纠正学生已有的认识错误，另一方面可以对学生的心理智力产生刺激，同时也是知识建构递进的需要·

教师提供两种解法·

解法1：f′（x）=x2+ax+2b·

依题意，方程x2+ax+2b=0的一个根大于0且小于1，另一根大于1且小于2·即0＜x1＜1，1＜x2＜2·则1＜x1+x2＜3，0＜x1x2＜2·由韦达定理得1＜-a＜3，0＜2b＜2，即-3＜a＜-1，0＜b＜ 1，则-2＜b-2＜-1，-4＜a-1＜-2·相除

解法2：f′（x）=x2+ax+2b·

依题意，方程x2+ax+2b=0的一个根大于0且小于1，另一根大于1且小于2·

不等式组表示的平面区域如图1所示，其中A（-3，1），B（-1，0），D（1，2）·

设C（a，b）为可行域（阴影）内一点·

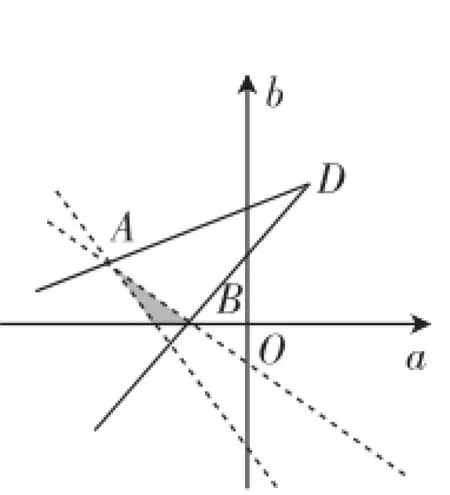
图1

教师提出问题1：用两种解法得到了相同的结论，都可以吗？

学生争辩后得出如下结论：解法1中，由0＜x1＜1和1＜x2＜2推出1＜x1+x2＜3和0＜x1x2＜2，不是同解变形，因此此解法是错误的；解法2应用了线性规划知识，准确地得到了不等式组所表示的可行域，此转化是等价的，解法是正确的·

问题2：为什么解法1得出的结果和正确的结果相同？

教师提示：用解法2的思路去思考解法1·

学生思考得出如下结论：由-3＜a＜-1、0＜b＜1得到的可行域是一个矩形BEAF（如图2），扩大的此矩形区域未能改变直线CD斜率的取值范围（C为可行域内的一点），因此得到的结果和正确的结果相同·

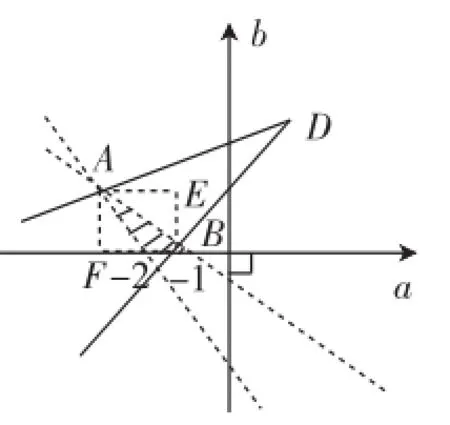
图2

教师：数学活动的实质就是思维的转化过程·在解题中，要不断改变解题方向，从不同角度、不同的侧面去探讨问题的解法，并寻求最佳方法，但在转化过程中保持转化的等价性是至关重要的·

教师在平时教学中要注意捕捉学生答题的思维缺陷，积极营造问题情境，发挥思维的监控作用，及时消除学生的错误认识，促进学生科学的认知结构的形成·

*本文系江苏省教育科学规划“十二五”重点资助课题《基于问题生成的动态课堂的实践研究》（课题编号：B-a/2011/02/05）的研究成果之一·

二、通过展示—评价—总结，优化学生的认知建构

学生是学习的主体，他们如果带着自己的认识、经验、猜想参与课堂活动，就使课堂呈现了人文性、合理性、生动性和丰富性，并在展示与交流中充分发挥学生各自的创造力，彼此的思维得到了碰撞、补充、优化·

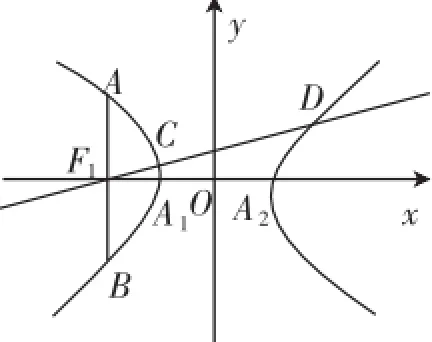
图3

教师先展示学生的方案1：假设存在这样的k·

则直线方程为y=k（x+c），代入双曲线方程，得：

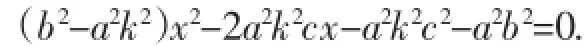
设C（x1，y1）、D（x2，y2）·

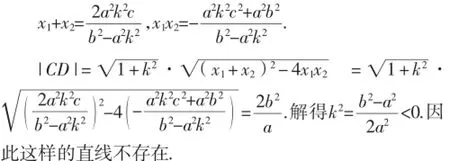
教师：利用弦长公式解决弦长问题，自然直接·还有别的方法吗？

教师：在求过焦点的弦的长时，运用定义可以简化弦长计算，优化了解题步骤，很好·还有更简便的方法吗？

沉默片刻，学生提出方案3：当两交点都在左支上时，最短的弦长为|AB|，当两交点在两支上时，最短的弦长为|A1A2|，即|CD|≥|A1A2|，所以要想存在k，使|AB|=|CD|，只需满足：|AB|≥|A1A2|⇒2a⇒b2≥a2，此条件不成立，因此这样的直线不存在·

该方案提出后，学生有的疑惑，有的惊讶，教师及时给予恳定：过焦点的直线与双曲线的交点在同一支上时，最短的弦长为2·交点在两支时，最短的弦长为

2a·并以此为契机，通过方案1、2给予证明，并通过数形结合给予了说明、解释，同时进一步启发学生思考在椭圆中有没有类似的规律性结论·

教学中教师要积极引导学生多方面、多角度思考问题的解决方案，并允许、鼓励学生大胆猜测，然后启发学生给予数学证明，逐步形成和发展数学应用意识，提高实践能力·

三、通过变式—训练—拓展，让学生建构更深刻

如果我们对课本中的例、习题进行特殊联想、类比联想和改变情境、推广引申，那么我们可以培养学生积极思考的习惯，达到深化理解的目的，同时也为发展学生的创新意识提供了有利条件·

案例3：苏教版必修5第96页第13题：已知正数x、y满

意图：此变式主要目的是当利用基本不等式求最值时，如果条件不满足，可考虑利用函数的单调性来完成·

意图：用字母代替具体的数字，综合了上述两题的方法，增加了对分类讨论思想的考查·

意图：把1+k2改为1-k2，增加对1-k2≤0时的讨论，加深了学生对形如y=x+（a∈R）的最值求解的一整套思路，进一步锻炼了学生分类讨论的能力·

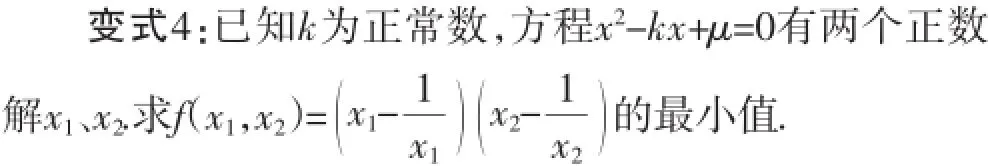
意图：把问题放入新情境中，提高了学生的问题转化意识及运用数学知识解决问题的能力·

在教师的引领下，通过变式训练，循序渐进，学生的学习热情高，学习的内驱力被激发，学生对形（a∈R）的最值问题的认识是深刻的，很好地培养了学生分类讨论的意识与能力·A