立足考纲明晰方向——对“考试说明”中一道示例的反思

☉江苏省西亭中学袁红

立足考纲明晰方向
——对“考试说明”中一道示例的反思

☉江苏省西亭中学袁红

“考试说明”既是高考命题的依据，也是指导师生复习备考的重要参考·学习研究“考试说明”，明确其强化什么，淡化什么，突出什么，回避什么，对明晰考试要求和把握复习方向有着重要意义；若脱离考试说明，则会使高考复习偏离方向·在“考试说明”中，根据某个数学模块的高考命题会举相应的示例，教师应如何利用好这些示例，使其示范作用更加突显？笔者以北京“2015年考试说明”中一道解析几何解答题为例，作如下反思：

例题（2014年北京卷理科第19题）已知椭圆C：x2+ 2y2=4·

（1）求椭圆C的离心率；

（2）设O为原点，若点A在椭圆C上，点B在直线y=2上，且OA⊥OB，求直线AB与圆x2+y2=2的位置关系，并证明你的结论·

通过观察近几年考试说明发现，每年都会更换部分典型示例·将2014年这道题放在样题中，也是因为此题精妙，可以通过探索特殊情况的状态，推测出普遍情况的结果·圆锥曲线是考查学生的运算能力、推理论证能力、分析问题和解决问题能力的有力工具·由于其计算量大、字母多的特点，在个性品质上能够培养学生战胜困难的信心，磨练出锲而不舍的精神·

一、反思示例的示范作用

自2010年北京实行新课标以来，高考命题中对圆锥曲线问题的考查通常以直线与圆锥曲线相交为背景，引入直线方程后，将其与曲线方程联立，消元后得一元二次方程，利用判别式及根与系数的关系等·而本题考查的是判断位置关系，很多学生看到这种题目不知所措，其实万变不离其宗·解析几何的本质是坐标表示与计算，有点写坐标，有线列方程，有关系就写式子，题目会有变化，但在变化之中又具有稳定性，要求我们必须掌握一些基本技能及解题的相应数学思想方法，同时这也是命题人要求考生了解数学的本质问题·

二、反思问题的通性通法

需要强调的是，虽然“考试说明”指出：“题型示例中的试题与2015年高考试卷的结构、形式、测试内容、题目排序、题量、难度等均没有任何对应关系，只是为了让考生对高考试题获得一定的认识·”但值得注意的是，题型示例中每道试题后面的“说明”，指出了该题考查的知识点和难易程度；题型示例中每道试题后面的“答案”，都体现了通性通法和常规解法·因此，“考试说明”中的题型示例仍然值得我们反思研究·

（2）由题可得，直线OA的斜率存在，设为k，则直线OA的方程为y=kx，OA⊥OB·

①当k=0时，A（±2，0），已知B（0，2），此时直线AB的方程为x+y-2=0或x-y+2=0，原点到直线AB的距离均为

综上所述，直线AB与圆x2+y2=2相切·

评析：“注重通性通法，淡化特殊技巧”是多年来数学“考试说明”中坚持的响亮口号，每年的试卷都体现了这一考查要求·在系统复习的时候，仅仅有知识的积累还不够，还要注重思想的领会和方法的归纳，特别是化归与转化的思想、分析与综合的方法及通性通法·这些思想和方法的获得，又全在于对数学知识网络的准确把握与灵活运用·

三、反思用最基本的方法解决最难的题目

高考命题遵循的是公平竞争原则，每个考生都会在平时练习遇到不同的题目，不要一眼看上去认为是“新题、难题”，从而产生畏难心理，甚至放弃解答，要知道所谓的“难题”可能只难在一点，“新题”只新在一处，由于畏难轻易放弃都会造成很大的遗憾·所谓的“难”或“新”，只是问题的表象，就其解法而言可能就是最基本的方法·本题判断直线与圆的位置关系，遇点设坐标，遇线设方程，从我们所熟悉的最基本的方法入手，即点到直线的距离与半径的关系入手·

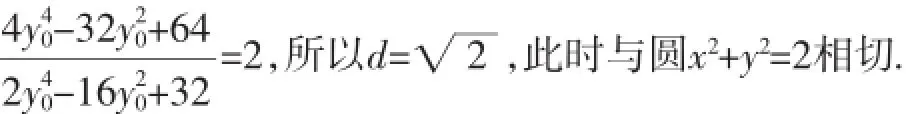
综上所述，直线AB与圆x2+y2=2相切·

评析：本解法从学生熟悉的角度入手，判断直线与圆的位置关系，可用最简单的方法，即圆心到直线的距离与半径的关系，可将问题顺利求解·这样充分考查了学生对所学基础知识的掌握程度，以及灵活应用其解题的能力·

四、反思解题思维的优化

在问题解决后，引导学生多角度、多层次、全方位地进行反思，反思解题方法是否可进一步优化，这样能使掌握知识的层次更具深度和广度，思维更深刻，使学生由会解一道题到会解一类题，把数学思维提升到一个由例及类的档次，形成有效的思维链·这样，有利于学生今后对解题途径做出快速选择，简化思维过程，缩短思维回路，提高思维的敏捷性和灵活性·

评析：对问题的探究不仅仅局限于正确结论的得出，而应从多角度、全方位对问题进行审视·上述解法从多想少算的角度为本题的解答指明了方向·

综上，著名数学教育家弗赖登塔尔教授指出：“反思是数学思维活动的核心和动力·没有反思，学生的理解水平不可能从一个水平升华到更高的水平·”可见，反思在数学学习中非常重要·通过反思学习可以帮助学生学会学习；可以使学生的学习成为探究性、研究性的活动；可以增强学生的能力，提高学生的创造力，促进他们全面发展·因此，教学中，教师应该重视学生的反思学习，积极创造反思条件，引导学生自觉反思·F