对2014年陕西卷理科第21题的研究

☉武汉大学附属中学齐黎明

对2014年陕西卷理科第21题的研究

☉武汉大学附属中学齐黎明

例1（2014年陕西卷理科第21题）设函数f（x）= ln（1+x），g（x）=xf′（x），x≥0，其中f′（x）是f（x）的导函数·

（1）令g1（x）=g（x），gn+1（x）=g（gn（x）），n∈N+，求gn（x）的表达式；

（2）若f（x）≥ag（x）恒成立，求实数a的取值范围；

（3）设n∈N+，比较g（1）+g（2）+…+g（n）与n－f（n）的大小，并加以证明·

笔者看到此题，脑海中想到了2010年和2005年湖北理科卷的压轴题，这三题都和欧拉常数有关，经过研究给出例1第（3）问的六种解法，同时给出三道真题之间的关系，并对命题本源进行了研究·

一、六种解法

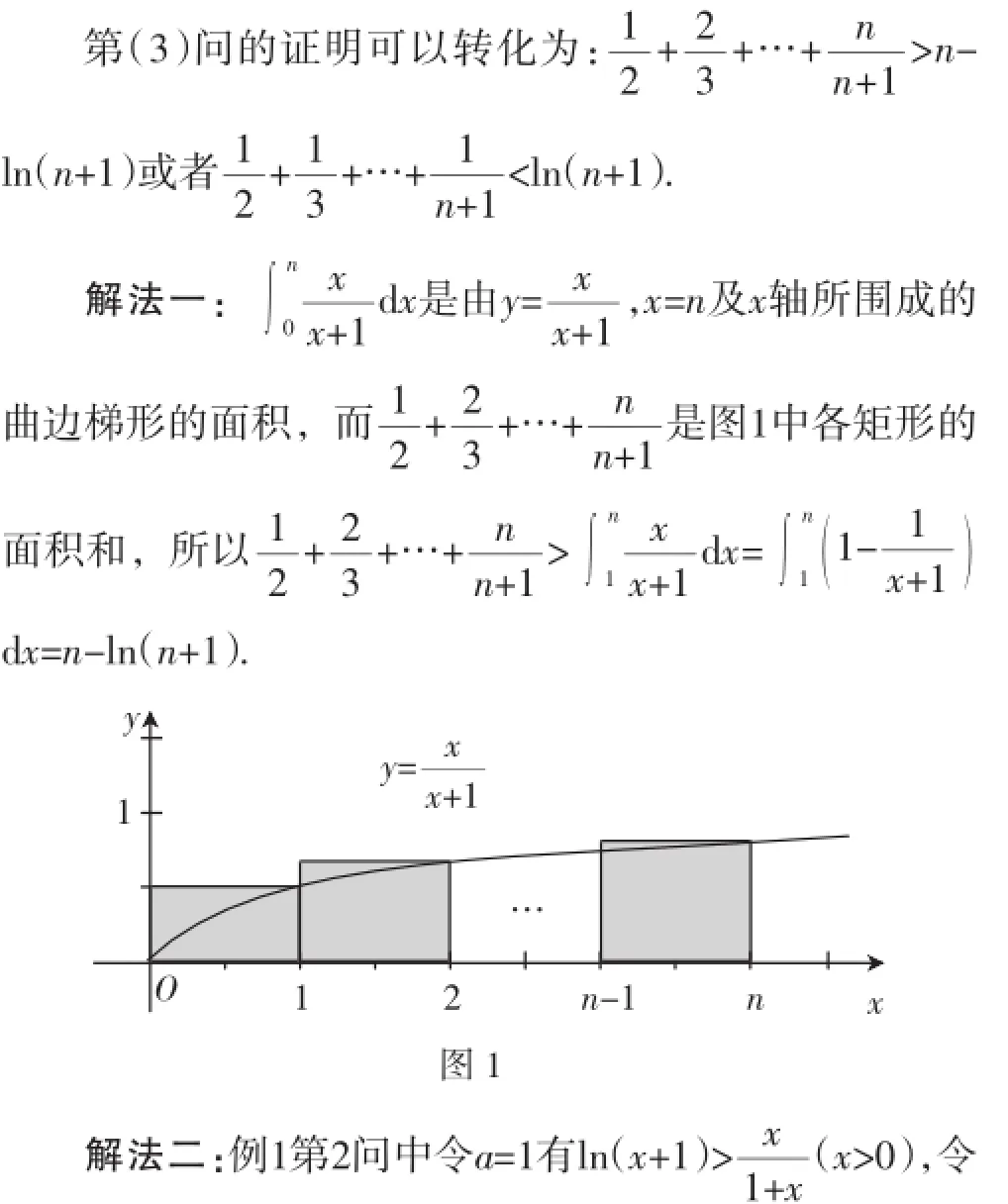
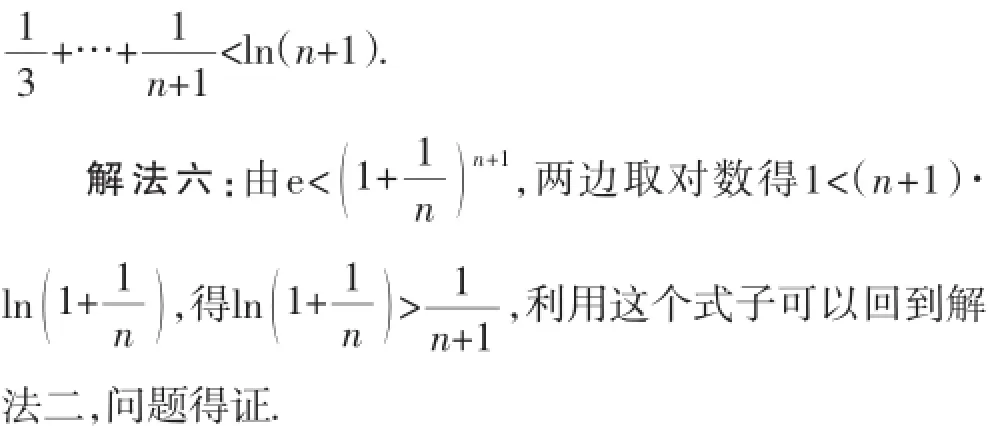
二、相关题研究

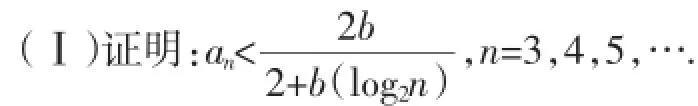
（Ⅱ）猜测：数列｛an｝是否有极限？如果有，写出极限的值（不必证明）·

三、三道真题溯源