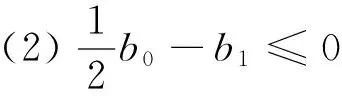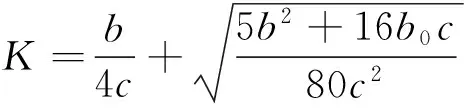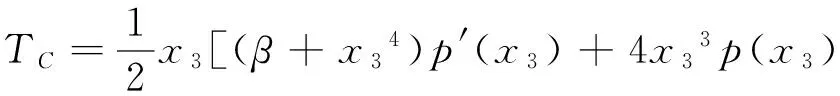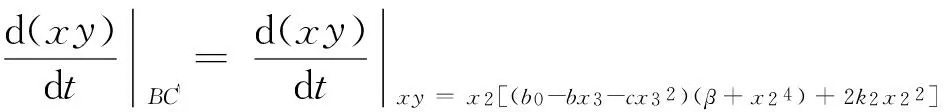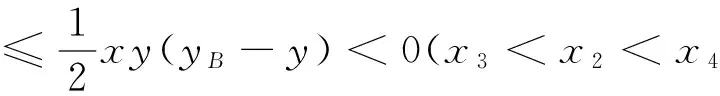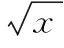两种群都有收获率的Holling-Ⅳ型系统的定性分析
王清娟
(福州大学阳光学院基础教研部, 福建 福州 350015)
两种群都有收获率的Holling-Ⅳ型系统的定性分析
王清娟
(福州大学阳光学院基础教研部, 福建 福州 350015)
研究了一类捕食者种群和食饵种群都有非常数收获率的Holling-Ⅳ型系统,分析该系统的平衡点性态,讨论极限环的不存在性、存在性条件.
Holling-Ⅳ型功能反应;定性分析;平衡点;极限环
(1)
(2)
近年来,许多学者研究Holling-Ⅳ型系统,取得很好的结论[4-6].文献[6]研究下列系统:
(3)
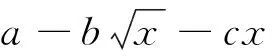
(4)
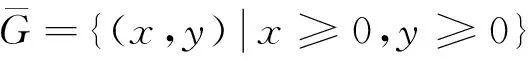

(5)
其中b0=a-q1E>0,b1=d+q1E>0.
1 平衡点的性态分析
根据系统(5)知:该系统的平衡点有3种情况:

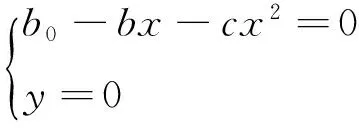
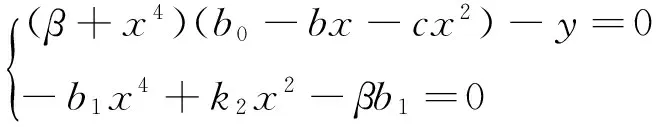
显然,O(0,0)总为系统的平衡点.
令p(x)=b0-bx-cx2,则
p′(x)=-b-2cx<0(x>0);
且p(x)=0有两个不相等的实根:
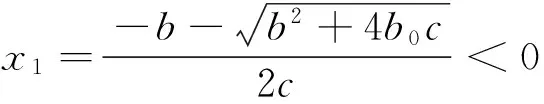
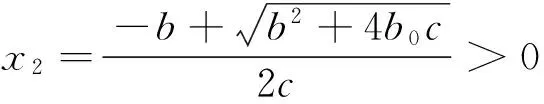
令q(x)=-b1x4+k2x2-βb1,则:
当k22-4βb12< 0时,q(x)=0无实根;
当k22-4βb12= 0时,q(x)=0有唯一正根:
当k22-4βb12> 0时,q(x)=0有两个正根:
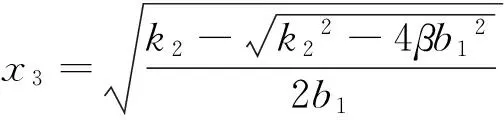

于是系统(5)可写为:
(6)
则系统(6)的平衡点对应的Jacobian矩阵为:

定理1 (Ⅰ) 平衡点O(0,0)总为鞍点.
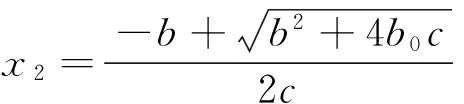
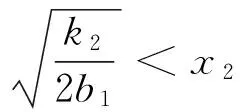
(Ⅳ)若k22-4βb12> 0,则
1)当x2 2)当x3 3)当x3 k2=b1(x32+x42),β=x32x42, yi= (β+xi4)p(xi)(i=3,4), 证明 (Ⅰ)系统在O(0,0)的Jacobian矩阵 其中p(0)=b0>0,q(0)=-βb1<0.则 所以O(0,0)为鞍点. (Ⅱ)若k22-4βb12< 0,则系统在A(x2,0)处的Jacobian矩阵 其中p′(x2)<0,q(x2)<0,则 所以A(x2,0)为稳定的结点. p(x0)>0,y0>0,q(x0)=0, q′(x0) = -4b1x03+ 2k2x0= 0, 故B(x0,y0)为正平衡点. 系统在B(x0,y0)处的Jacobian矩阵 显然DB=0,所以B(x0,y0)为高次奇点. (Ⅳ)若k22-4βb12> 0,则 1)当x2 2)当x3 y3>0,y4<0,p′(x2)<0,q(x2)>0, 故系统仅有一正平衡点:C(x3,y3). 此时对于平衡点A(x2,0),有 所以A(x2,0)为鞍点. 系统在C(x3,y3)处的Jacobian矩阵 则 又 所以DC>0,于是当TC<0(>0)时,C(x3,y3)为稳定(不稳定)的焦点或结点. 3)当x3 p(xi)>0,yi>0,(i=3,4). 故系统有两个正平衡点:C(x3,y3)与D(x4,y4).其中A(x2,0)是稳定的结点,证明同(Ⅱ);C(x3,y3)的性态同(Ⅳ)中的2). 系统在D(x4,y4)处的Jacobian矩阵 因为 故 所以D(x4,y4)为鞍点.证毕. 定理2 当系统(5)满足下列条件之一时: 则该系统在第一象限内不存在任何闭轨线. 证明 (1)取Dulac函数B(x,y)=x-1y-1,则 令 m(x)=-6cx5-5bx4+4b0x3-2βcx-βb, 则 m′(x)=-30cx4-20bx3+12b0x2-2βc, m″(x)=-12x(10cx2+5bx-2b0). 令g(x)=10cx2+5bx-2b0,则g(x)=0有一正根: 当0 g(x)<0,m″(x)>0; 当x>K时,有 g(x)>0,m″(x)<0. 定理3 若k22-4βb12> 0,x3 yB= [(b0-bx3-cx32)(β+x24) + 2k2x22] yC>yB, yB-y3= (b0-bx3-cx32)(x24-x34) + 2k2x22 又 x3 xy(-b1x4+k2x2-βb1) [1]匡奕群,邱梅青. 具常数存放的非线性功能反应捕食模型的定性分析[J]. 数学的实践与认识,2007,37(15):104-109. [3]王万雄,段永红,曹薇. 两种群都有收获率的HollingⅢ类模型的定性分析[J]. 生物数学学报,2009,24(6):674-680. [4]RuanShigui,XiaoDongmei.Globalanalysisinapredator-preysystemwithnonmonotonicfunctionalresponse[J].SIAMJournalonAppliedMathematics, 2001, 61:1445-1472. [5]王继华,曾宪武. 一类具有简化Holling-Ⅳ类功能反应的捕食-食饵模型的定性分析[J]. 数学杂志,2004, 24(6):701-705. [6]张敬,芦雪娟,何延治. 一类具有Holling-Ⅳ型功能性反应捕食模型的定性分析[J].延边大学学报, 2013, 39(2):93-96. [7]罗定军,张祥,董梅芳. 动力系统的定性与分支理论[M].北京: 科学出版社, 2001: 95-100. (责任编辑 穆 刚) Qualitative analysis of a predator-prey system with harvesting rate under Holling-Ⅳ functional response WANG Qingjuan (FoundationDepartment,SunshineCollege,FuzhouUniversity,FuzhouFujian350015,China) A predator-prey system with non-constant harvesting rate under Holling-Ⅳ functional response is investigated. The system’s equilibrium points are analyzed. The conditions for the nonexistence and existence of limit cycle are discussed. Holling-Ⅳ functional response; qualitative analysis; equilibrium point; limit cycle 2014-11-05 王清娟(1989—), 女, 福建莆田人, 助教, 硕士, 主要从事微分方程定性分析方面的研究. O175.12 A 1673-8004(2015)02-0048-04
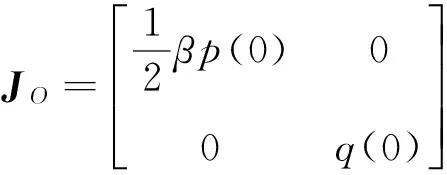
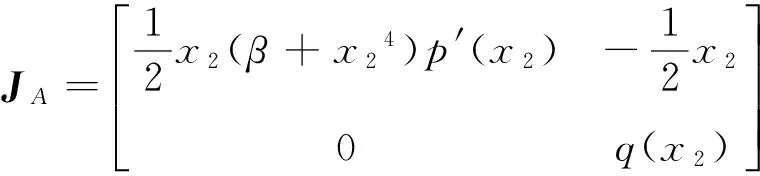

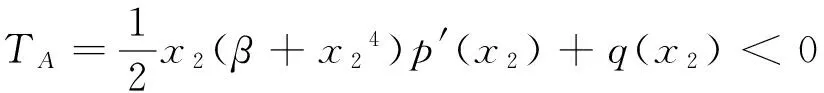
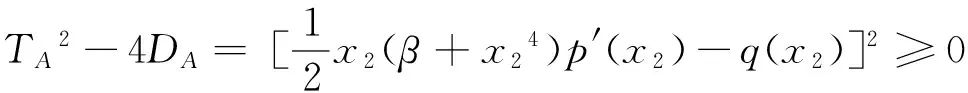
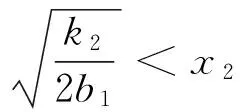
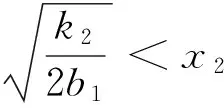

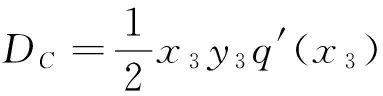
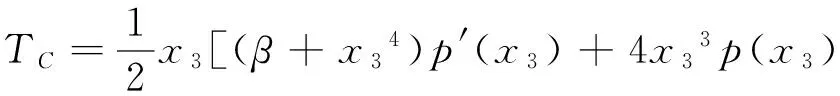
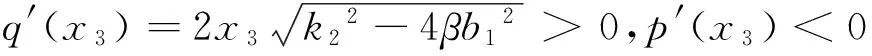
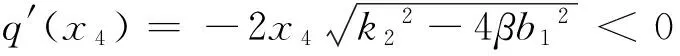
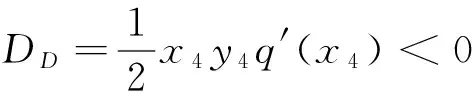
2 极限环的不存在性、存在性