小学数学教学中数学思想方法的有效渗透

江苏省滨海县正红镇中心小学 王 彬

实际上，数学课文内容不但包括了数学的结果，同时也包括了数学结果的形成过程以及数学思想方法。我们知道，数学知识是较为容易被忘记的，可是数学思维与方法则是可以长久保存下来。因此，在小学数学课堂活动中系统、有目的、有计划地将数学思想方法进行渗透，是非常有必要的。

一、利用情境创设渗透数学思想方法

数学知识源自于生活，且回馈于生活。利用情境的创设，老师结合课文有针对性地将生活本真提炼成数学问题，不仅体现了数学的实质，还能够让孩子在处理数学问题这一过程中深刻地理解生活。比如，当对“角的度量”这一内容进行教学时，教师可先创设一个教学情境，老师给孩子们展示坡度不一的3组滑梯：第一，坡度比较缓；第二，坡度适中；第三，坡度比较陡。然后发问：“请问你会选哪一组滑梯呢？这样选和什么相关呢？”孩子们通过探讨明白和坡度相关，所谓的坡度指的是斜面和地面间的夹角。此时老师把实物图形符号转化成“∠”、“∟”，孩子们感受了从实物及图形再到符号的一个转变过程，把生活实际化归为与角的大小相关的认识，轻松地向孩子渗透了数学对应的思想以及数学化归的思想。

二、在新知的学习探究过程中渗透数学思想方法

1.在算理、算法的揭示中渗透数学思想方法。

在数学计算的教学活动中，从表面来看，数学计算这一能力的培养及处理问题提供了一样工具。其实，老师只要懂得如何揭开计算教学活动中所含有的数学思想方法，仔细把握，加以灵活地设置，计算能力这一教学活动同样可以促进孩子的思维。

例如，在对“混合运算”这一课进行教学时：老师给孩子展示相关的香蕉图（图中有四盘香蕉，每一盘都有三个，还剩下两个单独的香蕉）。

T：算出共有多少个香蕉，应怎样求呢？

S：把两个部分结合起来算。

T：你可以解释下如此填的意义吗？

S：先算出4×3=12，然后算出12+2=14

T：仔细看看这一次列的算式与之前我们所学过的有什么区别吗？

S：这次的算式中不仅有乘法，还有加法。

T：动动脑筋看看如何画出它的样子？

数学教师通过对方块模型的利用，为孩子构建起了一个直观形象的“混合运算”的数学模式，全面运用了数学数形结合这一思想。孩子们通过“形”了解混合运算的本质结构，并且在填数建模这一活动中初步建立起模型思想。

2.在规律探索的过程中渗透数学思想方法。

在数学课堂教学过程中，数学规律是最为根本的知识体现。而要想揭示出小学数学规律少不了要有数学知识作支撑，但是更多的则要借助于数学思想方法。所以，在对数学问题进行探究的过程中，应该认真挖掘出数学的思想方法。

如，在对苏教版四年级“找规律”这一课进行教学时候，教师可先为学生呈现：一条总长度为20m的马路的一侧，在路测每隔2m种植一棵树木，请问能种多少棵呢？当孩子们面对这个问题的时候纷纷讨论：究竟有多少棵树呢？这个时候，老师在给孩子们呈现图1（如下图1），先让孩子懂得“每2米”便是种树的“间隔”。然后让孩子们动手画画，拿实物去摆一摆，接着议一议，当孩子在历经这一过程后，再把孩子们探讨的结果概括成图2（如下图2）的三种情况。引导孩子在进行观察之后归纳出：

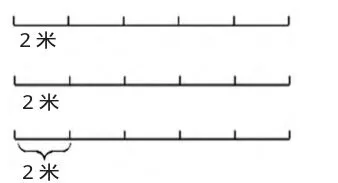
图1

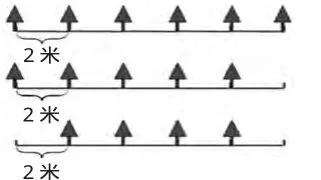
图2

如果两端都进行种植，能种六棵，若一端种植一端则不种植，能种五棵，假如两端都不进行种植的话就只能种四棵了。然后引导孩子作进一步的讨论：除每2米植树一棵外，还能够怎样种植呢？孩子们经过了以上的探索思路与过程，很快受到启发，便能迅速地得出每4米、5米、10米、20米种一棵的结果。在这个时候，老师及时进行引导，让孩子进一步加以观察、归纳和总结出种树的相关规律。借助此类的探索性的活动，向孩子们渗透了探究归纳、数型结合以及数学建模等的思想方法，让孩子们感受到了数学思想方法在数学规律探究中的关键作用。

三、在练习的巩固、反馈中渗透数学思想方法

在数学课程教学活动中，课文习题的求解过程，同样是数学思想方法的获取过程和应用过程。孩子在做练习时，不但能够巩固及深化已经学习的知识内容和数学学习的思想方法，还可以从中总结与提炼出一些新型的数学思想方法。比如，在一年级的孩子学完了20以内的加法之后，教师可以引导他们完成下列的习题。如图所示：在图中描出横排和竖排上两个数相加等于10的格子，再分别描出相加等于6，9的格子，你能发现什么规律？

经过此种的练习可以帮助孩子们熟练作出20以内的加法，有效地渗透了数形结合的数学思想。同时数值和图形相结合能够帮助孩子们在今后学习坐标系以及图像时可以有一个更好的学习状态与基础。

总而言之，在小学数学课程教学中，有效渗透数学思想方法是非常重要的。数学老师应该结合数学教学目标，根据数学课程内容，巧妙设计好教学方案，促使进一步提高孩子们的数学素养。

［1］中华人民共和国教育部.全日制义务教育数学课程标（2011年版）[S].北京：北京师范大学出版社.2012

［2］张丹.小学数学教学策略[M].北京：北京师范大学出版社.2010