两个重要极限教法探究

福州海峡职业技术学院 黄新丽

两个重要极限是《高等数学》第一章函数的极限与连续中的重要内容.它不仅是极限运算的重要工具，也是微分学中推导初等函数导数公式的工具，在整个高等数学课程中有着重要作用.本文既考虑到数学学科的科学性，又针对高职班学生的接受能力和理解程度，力求教学内容涵盖大纲，易学，实用.

一、学情分析

1.学生已经具备了函数的基本知识，掌握了函数极限的概念和极限的四则运算法则；

2.学生基础参差不齐，思维不够灵活，求极限时思路混乱；

3.排斥过多的理论知识，更喜欢知识的应用.

二、新课引入

大学生是具备独立思考能力和分析问题能力的个体，相比被动的“填鸭式”的教学方法，启发式的教学方法更能吸引学生的学习兴趣.因此，本文将数学建模的思想融入到教学过程中，采用问题驱动法和案例教学法，以银行复利问题引入，激发学生学习兴趣，加强数学与实际生活的联系.

引例2 假设有本金A0元，银行年利率为r，那么第t年末能得到本息和A为多少钱？

解：若每年结息一次，

第一年末的本息和为：A0（1+r）

第二年末的本息和为：A0（1+r）2

…

第t年末的本息和为：A=A0（1+r）t

三、公式的证明

两个重要极限的数学证明较为复杂，结合高职高专学生实情，在教学中应淡化繁琐的推导和证明，以应用为向导，以能力为目标，使学生获得必需、够用的数学知识.淡化证明过程的同时，帮助学生理解两个重要极限.本文运用Matlab软件绘出函的函数图形，然后从极限的定义出发，引导学生探索得出两个重要极限的结论.

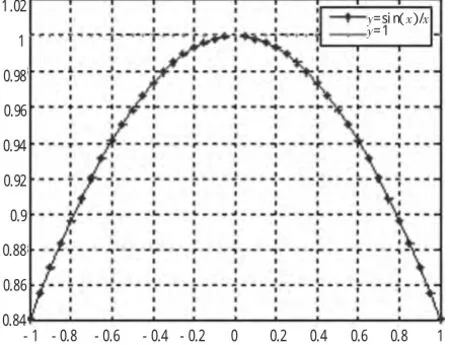
图（1）

x→0时，sixnx

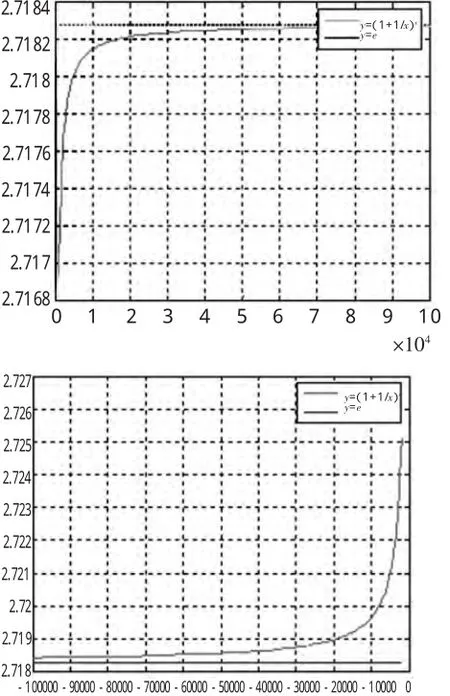
图（2）

四、应用举例

在学生掌握了两个重要极限的结论后，关键在于帮助学生学会应用公式来求定型的极限，这也是本教学内容的难点.本文提出“变量形式不变性”的思想，将重要极限结论进行推广，并引导学生对具体的应用情况进行总结.

这个重要极限公式可适用于求解多种含三角函数的“0”型的极限.0

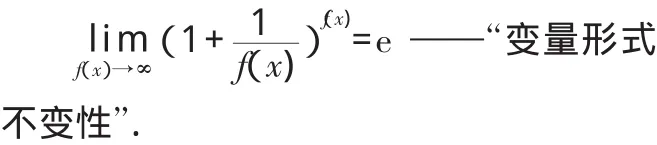
这个重要极限公式可适用于求解“1∞”型的极限.

[1]王梦洁.对两个重要极限的新认识[J].科技世界.2013(2)：93-94

[2]张先荣.浅谈两个重要极限的重要性及应用 [J].濮阳职业技术学院学报.2013.26(3)：149-151

[3]赵树嫄.微积分[M].北京：中国人民大学出版社.2013.5