基于EVT-Copula的操作风险度量

宋加山， 张鹏飞， 王利宏， 王 彪

(1.西南科技大学 经济管理学院，四川 绵阳 621010； 2.中国科学技术大学 管理学院，安徽 合肥 230022)

基于EVT-Copula的操作风险度量

宋加山1， 张鹏飞1， 王利宏1， 王 彪2

(1.西南科技大学 经济管理学院，四川 绵阳 621010； 2.中国科学技术大学 管理学院，安徽 合肥 230022)

新巴塞尔协议把操作风险纳入风险量化和监管领域，要求国际活跃商业银行开发的操作风险计量模型能够处理操作风险损失概率分布厚尾特征。并明确建议通过损失分布法等高级方法来度量操作风险。而使用损失分布法的计量模型没有考虑业务线/事件类型之间的相关性，这与实际情况是不相符合的。为此本文运用极值理论模拟损失分布，建立计算操作风险总VaR值的EVT-Copula模型，并在此基础上运用Copula函数度量银行各类业务操作风险之间的相依性，得到整体VaR值的模拟值。

Copula函数；极值理论；在险值

1 引言

2004年正式颁布的巴塞尔新资本协议明确提出商业银行面临三大主要风险：信用风险、市场风险和操作风险，也正式将操作风险纳入了监管范围并且为其配置相应的监管资本。同时建议国际活跃商业银行采用内部法、损失分布法、极值理论等更具风险敏感性的高级法(Advanced Measurement Approaches, AMA)度量操作风险。所谓操作风险就是指由于不适当或失败的内部过程、人员、系统或外部事件所导致的直接或间接损失的风险，其最大特征是低频高危的极值事件，针对这类事件独特的风险特征，通常引入极值理论对操作风险进行度量，以探讨极端事件的极限分布，即尾部收益行为。而在运用损失分布法度量操作风险过程中要求先明确业务线/事件类型组合，计算每个业务线/事件类型组合的VaR(Value-at-Risk，VaR)值，然后对所有的业务线/事件类型值简单加总求得操作风险总的资本要求。但经典的VaR极值方法局限性在于其风险测度不一定满足次可加性。从国内外在该领域的研究进展来看，国外学者研究了通过相依结构来度量风险，例如Bocker和Kluppelberg[1]利用Levy Copula对不同业务线之间的相依结构进行建模从而实现多维角度精确度量操作风险。Clemente和Romano[2]基于传统的频率程度模型对不同业务线并运用保险数据进行了实证对比分析。而国内大多数研究都假设各类操作风险之间是完全相依的，计算操作风险总VaR值时，只是把各类操作风险VaR值简单相加，这与实际情况是不相符的。为此本文对从公开媒体报道收集的操作风险损失数据进行实证分析，通过刻画每个业务线/事件类型的损失分布，在此基础上运用Copula函数度量不同业务线/事件类型组合的损失相依结构，得到总的操作风险VaR值。

2 操作风险损失模型

2.1 Copula函数在金融中的应用情况

金融市场的风险管理和防范是Copula模型的一个重要应用领域，近年来，Copula理论在风险管理的应用上取得了长足的进展。最早将Copula理论引入金融风险管理的是Embrechts等[3]，随后很多学者对这一领域进行了深入的研究，如Rosenberg和Schuermann[4]运用Copula理论研究了市场风险、信用风险和运作风险的风险聚合问题，并与其他模型进行了对比，结果表明由Copula模型计算得到的VaR值最接近经验VaR值；Martin[5]系统地描述了如何通过Copula模型来构造投资组合的信用风险。综上来看，Copula理论作为相关性分析和多元统计分析的工具，可以捕捉到变量间非线性、非对称的相关关系，特别是尾部的相关关系，因此本文将其和极值理论结合来构建我国商业银行操作风险损失模型。

2.2 建立损失分布模型

巴塞尔新资本协议将操作风险分为八大业务线和七大风险事件，其核心问题在于对所有不同的业务线和事件类型的多维组合进行建模。为此本文考虑建立一个的复合Possion分布[6]

(1)

其中i=1,…,r,j=1,…,s；N(i,j)是在一年以内每一业务线和事件类型的损失事件数目的随机变量；Xk(i,j)是第k次业务线/事件类型的损失程度，令X0(i,j)=0。

N(i,j)是一个Possion分布，其分布如下

假设每年发生操作风险的次数服从负二项分布

一般用对数正态来模拟损失分布，假设随机变量Xk(i,j)服从独立同分布的累积分布函数为Fi,j，Fi,j是一个对数正态分布

其中x>0。

但是对数正态分布往往低估风险损失，为此采用极值理论修正其尾部分布，假设每次风险发生的风险损失程度的分布左部和中部为对数正态，而尾部则由EVT理论确定为如下分布

其中Nu(i,j)是在业务线i/事件类型j中超过阈值u(i,j)损失额度的数目；Ni,j是业务线i/事件类型j中损失数据中总的数目；u(i,j)，β(i,j)，ξ(i,j)分别是广义帕累托分布(GDP)的位置、刻度和形变参数，可以由大于阈值的数据估计得到。估计方法见文献[7]。

3 EVT—Copula模拟

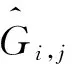
令t-Copula的密度表达式为

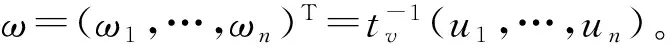
其参数估计步骤如下：

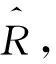
第二,将样本数据ui,1,ui,2,…,ui,T作变换，得到具有标准边缘分布的样本数据

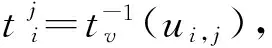
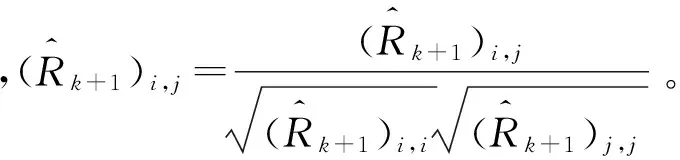
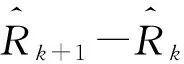
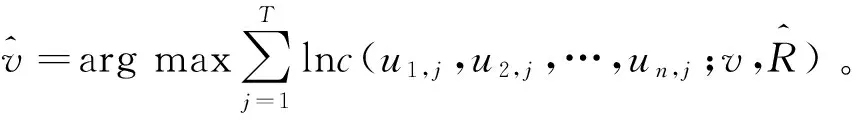
根据t-Copula的定义，得到蒙特卡罗模拟算法：

(1)计算R的Cholesky分解A；

(2)随机模拟n元独立的随机样本z，使z满足z=(z1,…,zn)′～Nn(0,1)；

(3)令y=Az；

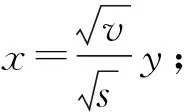
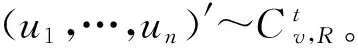
这样就估计了t-Copula的蒙特卡罗模拟，其具体步骤见Masha和Naldi的研究[8]。

4 实证分析

4.1 样本分析

为验证模型的有效性，本文选取了从公开媒体收集的我国商业银行操作风险损失数据作为样本数据，时间长度为2000年至2013年共330条数据，其中最大损失金额为30亿元，最小损失金额为0.15万元。对损失数据按照巴塞尔新资本协议关于操作风险业务线和事件类型的划分标准，以事件主要特征进行分类组合整理，构造了56种组合，通过对数据的初步分析，内部欺诈和外部欺诈两类风险以及在商业银行业务、零售银行业务、支付和结算等三类业务组合在全部操作风险事件中所占比例约为85%，造成的损失所占比例约为80%，为此本文主要考虑内部欺诈和外部欺诈两类风险和商业银行业务、零售银行业务、支付和结算等三类业务线组合的操作风险情况来进行分析。

从图1中可以看出内部欺诈和外部欺诈两类风险事件呈现明显的厚尾状态。这也说明了EVT在操作风险建模中的可行性。

图1 内部欺诈和外部欺诈与零售银行业务组合的QQ图

4.2 实现步棸

本文把从2000年到2013年发生的操作风险损失事件以内部欺诈和外部欺诈两类风险以及在商业银行业务、零售银行业务、支付和结算业务等三类业务线的组合用i予以标示，每年都能得到一个次数n(i)。由此可以模拟得到一年损失Possion分布，其参数为λ(i)。从每年的损失额度Xk(i),k=1,…,n(i)，可以模拟得到累积损失分布函数Fij，最后通过每年的损失总和可以模拟得到第i个业务线的总损失分布函数，以此计算出t-Copula的参数。

通过极大似然估计得到EVT的参数β(i)和ξ(i)，同时运用矩估计可以求得Possion分布的参数估计。

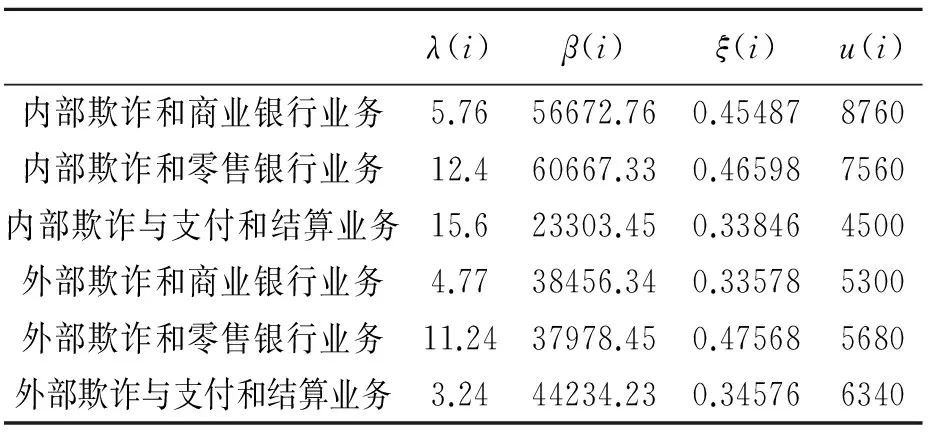
表1 参数估计

通过t-Copula的Monte Carlo模拟得到密度函数的两个参数，其中自由度V=10，相关矩阵R显示内部欺诈和零售银行业务、内部欺诈和商业银行业务、内部欺诈与支付和结算业务三者之间的相关系数分别为0.75、0.74、0.71，呈现出较高的相关性。为此，需要加强对内部欺诈和零售银行业务、内部欺诈和商业银行业务以及内部欺诈与支付和结算业务的监管，以提高我国商业银行操作风险管理水平。

4.3 结果分析

表2中第2列表示业务线按照简单相加法得到的不同置信水平下的在险值，第3列表示引入t-Copula后得到的在险值，第4列表示两种方法确定的在险值相较减少的百分比；可以明显看出，基于t-Copula确定的在险值比传统简单直接相加法所得在险值减少8%以上，这说明应用t-Copula度量在险值，可以节约大量的监管资本。

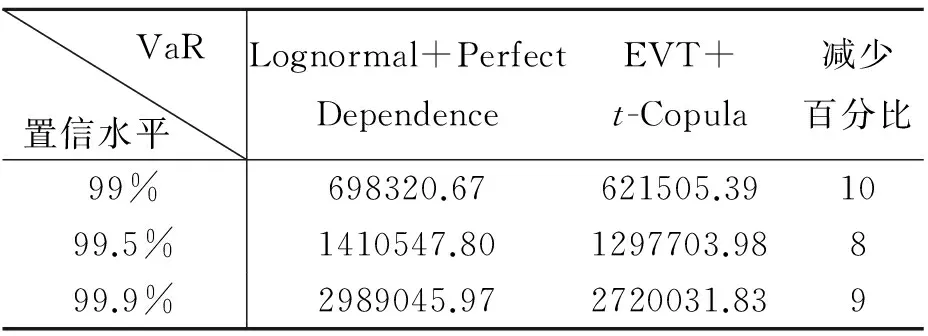
表2 不同置信水平下VaR的比较

4.4 结论与建议

(1)应用t-Copula度量在险值可以减少大量监管资本。本文基于对传统假设操作风险之间完全相依关系与实际不吻合的情况，运用极值理论模拟损失分布，通过引入Copula函数度量不同业务线/事件类型中的损失相依结构，并从公开媒体报道收集的操作风险损失数据进行实证分析，结果表明基于t-Copula度量的在险值比传统简单直接相加法减少8%以上。

(2)对商业银行操作风险资本计量具有现实指导意义。当前商业银行资本计量在信用风险、市场风险等领域比较成熟，研究成果和量化测算模型较多，在行业内应用较为广泛；而本文通过引入Copula函数度量不同业务线/事件类型组合的损失相依结构，得到的操作风险资本计量模型更为精巧；而且在现有研究成果中相对较少，此研究对商业银行操作风险资本计量具有现实指导意义，有利于提高我国商业银行操作风险管理水平。

(3)能在一定程度上减少银行操作风险资本计量过高的担忧。操作风险数据的收集非常困难，媒体披露的风险事件仅仅是冰山一角，即使在银行内部，出于种种原因，也不愿意披露，甚至很多也知情不报，这在一定程度上影响模型结果可靠性。但如果我国商业银行能收集和积累一定量的数据，再结合此类模型度量风险，可在一定程度上免除银行操作风险资本计量过高的担心，引导更为客观地记录和披露操作风险事件。

(4)操作风险防范是我国商业银行风险管理的一个重点和弱点。目前国外先进银行机构在信用风险、市场风险和操作风险的度量模型、方法上研究成果较多，而国内操作风险研究和应用相对滞后。在全球化进程中，特别是新巴塞尔资本协议对资本充足率提出更高要求的情况下，中外银行必须站在一条起跑线才能更为公平竞争，为此，应加强我国商业银行操作风险度量与管理，客观反映操作风险状况。

[1] Bocker K, Kluppelberg C. Multivariate models for operational risk[R]. Preprint, TU Munich, 2006. 7-13.

[2] Clemente A, Romano C. A copula-extreme value theory approach for modelling operational risk[R]. Working Paper, University of Rome “La Sapienza”, 2003.

[3] Embrechts P, McNeil A, Straumann D. Correlation: pitfalls and alternatives[J]. Risk, 1998, 5(12): 69-71.

[4] Rosenberg J, Schuermann T. A general approach to integrated risk management with skewed, fat-tailed risks[J]. Journal of Financial Economics, 2006, 79: 569- 614.

[5] Martin R. Credit porfolio modeling handbook[M]. First Boston: Credit Suisse, 2004.

[6] 杨旭.多变量极值理论在银行操作风险度量中的运用[J].数学的实践与认识，2006，36(12):193-197.

[7] 陈守东,胡铮洋,孔繁利.Copula函数度量风险价值的Monte Carlo模拟[J].吉林大学社会科学学报，2006，46(2):85-91.

[8] Mashal R, Naldi M. Pricing multiname credit derivatives: heavy tailed hybrid approach[DB/OL].http://www.columbia.edu/rm586, 2002- 01-16.

Operational Risk Measurement Based on EVT-Copula

SONG Jia-shan1, ZHANG Peng-fei1, WANG Li-hong1, WANG Biao2

(1.CollegeofEconomicsandManagement,SouthwestUniversityofScienceandTechnology,Mianyang621010,China; 2.SchoolofManagement,UniversityofScienceandTechnologyofChina,Hefei230022,China)

The New Basel Capital Accord takes operational risk into the region of risk quantification and supervision, demands operational risk measurement models developed by active commercial banks can be capable of handling the situation of thick tailed distribution on probability distribution losses in the operational risk, definitely suggests measuring operational risk by high-level approaches such as losses distribution. And yet the measurement model of losses distribution leaves out of consideration of the relevance between business line and event type, which is not conform to the actual situation. For this reason, this paper builds a EVT-Copula Model of total value VaR to calculating operational risk, using the extreme value theory to simulate losses distribution, to get an analogue value of the whole VaR value.

Copula function; extreme value theory; Value-at-Risk

2013- 05-28

四川省科技厅软科学研究计划资助项目(2013ZR0097)；西南科技大学科研基金资助项目(13sxt012)

F832.2

A

1003-5192(2015)03- 0070- 04

10.11847/fj.34.3.70