基于抗堵塞能力的路网分区路径选择研究
苏 兵, 程 晨, 徐 阳
(西安工业大学 经济管理学院,陕西 西安 710032)
基于抗堵塞能力的路网分区路径选择研究
苏 兵, 程 晨, 徐 阳
(西安工业大学 经济管理学院,陕西 西安 710032)
针对路网中任意路段都有可能发生堵塞的情形,结合交通均衡分配原则,本文提出路网分区效果度量指标——基于路网交通均衡分配的分区抗堵塞能力变化因子,即基于路网交通均衡分配的分区后各子区域平均抗堵塞能力与分区前整个路网抗堵塞能力的比值。在此基础上,以指标最小为目标,建立将城市路网划分为2个子区域的最优分区路径选择模型,并设计算法求解,为交管部门进行路网分区管理提供依据。
路网分区;交通均衡分配;分区抗堵塞能力变化因子;最优分区路径
1 引言
随着城市交通经济的快速发展,城市交通网络日益复杂,路网交通量日益增大,给城市路网整体管理带来很大的困难。路网分区是指交管部门根据路网结构和交通流特性,用一条或几条路径将城市道路网络划分为若干个交通区域实行分区管理,路网分区是提高交通管理效率的主要手段。
现有城市路网分区原则主要有三类:第一类结合路网拓扑结构进行分区。一是使每个子区域的人口数量、土地面积相近,路网上的节点及边各有归属,每一条边和节点都被某个区域管辖且各区域相互独立[1]。二是使得每个子区域的用地特征相似,如按旧城区、工业新区和居住新区进行划分[2],并在此基础上,进一步按公交线网密度、机动车和非机动车停车设施以及慢行设施规模等交通设施供应水平将城区划分为核心居住区和外围居住区[3]。第二类是在路网拓扑结构分区的基础上结合路网交通量进行分区。一是考虑节点间交通需求量、节点上到达流量等指标,以满足出行交通量相同或相近的目标进行路网分区[4,5]。二是考虑饱和度、信号周期等指标对路网进行基本区域的划分,将同时大于最大饱和度或小于最小饱和度的相邻交叉口和信号周期相近的相邻交叉口合并,再结合路网可靠度,对所划分的基本区域进行评价和筛选,从而确定最终的交通控制子区[6]。三是考虑交通波理论,建立路段排队最远点模型,即排队最远点到停车线的距离与路段长度的比值接近于1时,该路段对应的交叉口合并,进而针对比值小于1且路段流量较大的情形下,提出流量-距离原则,将路段流量与路段距离比值最大的路段对应的交叉口进行合并,以实现路网分区[7]。第三类结合交通均衡分配原则进行分区,使分区后各子区域最优出行时间之和与分区前整个路网的系统最优出行时间的比值最小[8]。然而,在实际中,路网中的路段经常会发生堵塞而不可用,现有研究并没有讨论路段堵塞情形下的路网分区问题。
本文针对路网中任意路段都有可能发生堵塞的情形,结合交通均衡分配原则,从路网分区前后抗堵塞能力变化的角度提出分区效果度量指标——基于路网交通均衡分配的分区抗堵塞能力变化因子,即基于路网交通均衡分配的分区后各子区域平均抗堵塞能力与分区前整个路网抗堵塞能力的比值。在此基础上,以指标值最小为目标,建立将路网划分为2个子区域的最优分区路径选择模型并给出算法,为交管部门进行路网分区管理提供依据。
2 问题描述与基本假设
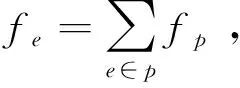
为方便讨论,给出以下基本假设。
(1)交通量是任意可分的;
(2)所有出行者均服从管理者制定的交通流分配原则;
(3)分区前,管理者选择系统最优分配原则分配整个路网内的交通流量;
(4)堵塞一旦发生就不可恢复,且堵塞发生后,管理者在其管辖的区域依然选择系统最优分配原则分配交通流量;
(5)路网中去掉任意路段之后仍然连通。
3 基于路网抗堵塞能力的分区效果度量指标
当路网上的任意一条路段发生堵塞时,该路段将不可用,不论按照哪种交通均衡分配原则重新分配交通流量均会导致该路段堵塞前后的路网总出行时间发生变化,不同路段堵塞带来的这个变化是不同的,因此可用这种变化的大小来度量路段的抗堵塞能力。路网中存在多条路段,路网中所有路段的平均抗堵塞能力可以反应整个路网的抗堵塞能力。因此,考虑任意路段都有可能发生堵塞情形下的路网分区,可以首先计算出分区前整个路网的抗堵塞能力,再计算出分区后各子区域的平均路网抗堵塞能力,将两者进行比较,就可以度量分区效果的好坏,从而提出基于路网交通均衡分配抗堵塞能力的分区效果度量指标。
以下分别给出基于路网交通均衡分配的路段抗堵塞能力度量指标、路网抗堵塞能力度量指标和分区效果度量指标的定义。

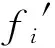
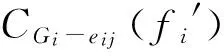
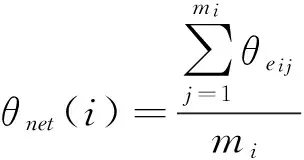
根据定义1和定义2可知,θnet(i)越小,路网Gi中所有路段基于路网交通均衡分配的抗堵塞系数均值也就越小,即路网Gi基于路网交通均衡分配的抗堵塞能力越大。
路网划分之前,可以计算出整个路网基于路网交通均衡分配的路网抗堵塞能力,路网进行区域划分后,整个路网所管辖的路段被分到各个子区域中去管理,根据定义2,每个子区域都可计算出基于路网交通均衡分配的子区域抗堵塞能力,因此,针对分区前后路网抗堵塞能力的变化,给出分区效果度量指标如下。
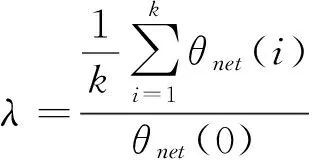

4 最优分区路径选择模型
第3节提出分区效果度量指标——基于路网交通均衡分配的分区抗堵塞能力变化因子,本节将讨论如何以指标值最小为目标,在路网中选择最优分区路径将路网划分为2个子区域。
为解决上述问题,首先给出以下假设。
(1)分区路径的起讫节点是交通路网边界上的点对;
(2)各子区域交通相互独立,且分区路径上所有路段属于同一区域管辖;
(3)所划分2个子区域管辖的路段数量之差不大于分区路径上的路段数量;
(4)所划分子区域中至少存在1条路段删除后,子区域仍然连通。
首先给出分区路径的定义。
4.1 分区路径
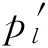
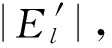
(2)该路径所划分的子区域中至少存在1条路段删除后,子区域仍然连通,即满足|P″|≥2,其中P″表示子区域中某起讫点的路径集合。
根据以上定义可知路网中具有多条分区路径,但最优分区路径一定是导致分区效果最优的路径,即导致基于路网交通均衡分配的分区抗堵塞能力变化因子值最小的分区路径,以下给出最优分区路径的定义。
4.2 最优分区路径
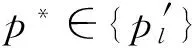
5 最优分区路径选择模型求解
由上节的分析可知,首先需要找出分区路径,然后找出分区前后路网抗堵塞能力变化最小的分区路径即为最优分区路径。求解方法如下。
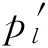
第1步从边界点集V″中取尽不重复的点对(va″,vb″),其中a=1,2,…,k-1;b=a+1,…,k。
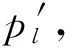
第3步令l=1。



第7步根据(OD)2l,由系统最优分配原则得到区域G2l的最优交通分配流量f2l和路网总出行时间CG2l(f2l)。
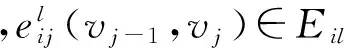
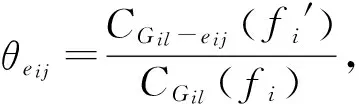
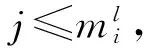
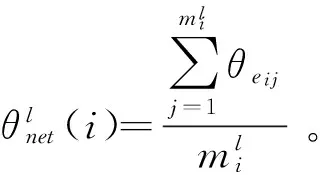
第12步令i=i+1,如果i≤2,则转到第9步;否则,转下一步。
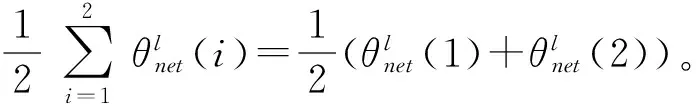
第14步令l=l+1,若l 第15步根据系统最优分配原则计算整个路网的最优交通分配流量f*和路网出行总时间CG0(f*)。 第16步令j=1,e0j(vj-1,vj)∈E为删除路段,根据系统最优分配原则计算路网总出行时间CG0-e0j(f*′)。 第18步令j=j+1。如果j≤m,则转至第16步;否则,转下一步。 城市路网分区给道路交通带来很大的影响,如何选择分区路径是路网分区的关键。本文针对路网中任意路段都有可能发生堵塞,结合交通均衡分配原则,从路网分区前后抗堵塞能力变化的角度对城市路网进行分区,设计分区效果度量指标——基于路网交通均衡分配的分区抗堵塞能力变化因子。经过分析得出指标值越小,分区效果越好。以指标值最小为目标,给出将路网划分为2个子区域的最优分区路径选择方法,为城市路网分区提供依据。 [1] Ding C, Choi K, Kim T J. GIS-based traffic analysis zone design[A]. Proceedings of the Third International Conference in Computes in Urban Planning and Urban Management [C]. Atlanta, Georgia, USA, 1993. 7. [2] 钱寒峰,杨涛,杨明.城市交通规划与土地利用规划的互动[J].城市问题,2010,(11):21-24. [3] 过秀成,孔哲,杨明.城市交通分区体系构建研究[J].现代城市研究,2010,(1):16-20. [4] Zografos K G, Routsopoulos K N, Vasilakisi G M. A real-time decision support system for roadway network incident response logistics[J]. Transportation Research C, 2002, 10(1): 1-18. [5] Zong T, Thomas U. System partition technique to improve signal coordination and traffic progression[J]. Journal of Transportation Engineering, 2007, 133(2): 119-128. [6] 尚德申,石建军.交通控制区域动态划分研究[J].道路交通与安全,2007,(1):27-29. [7] 陈晓明.交通控制子区动态划分指标研究[D].长春:吉林大学,2007. [8] Su B, Fang L, Yang Q. How to finding a path to zoning a traffic network efficiently[J]. Information Technology Journal, 2012, 11(4): 551-555. Finding a Zoning Path Based on Anti-block Ability in an Urban Traffic Network SU Bing, CHENG Chen, XU Yang (SchoolofEconomicsandManagement,Xi’anTechnologicalUniversity,Xi’an710032,China) Each edge of the network has possibility of blockage. In this paper, we present a parameter-zoning anti-block ability change factor based on traffic equilibrium assignment for measuring the zoning effect, the ratio between the average anti-block ability of sub-networks and the anti-block ability of whole network based on traffic equilibrium assignment. Minimizing the parameter, a model for finding zoning optimal path to divide a network into two sub-networks is established, and shows an algorithm. road network zoning; traffic equilibrium assignment; zoning anti-block ability change factor; zoning optimal path 2014- 07- 14 国家社会科学基金资助项目(13BGL156);教育部人文社会科学基金资助项目(12YJAZH121);长江学者和创新团队发展计划资助项目(IRT1173);陕西省教育厅基金资助项目(2013JK1118);西安工业大学校长基金资助项目(XGYXJJ0539) U491 A 1003-5192(2015)03- 0061- 04 10.11847/fj.34.3.61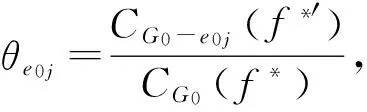
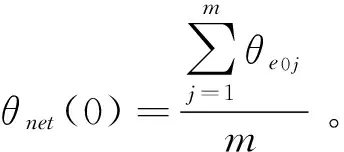
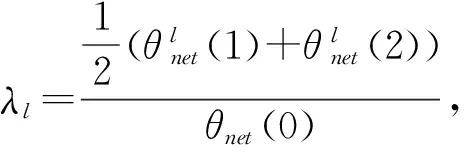
6 结论

