统一组织管理下的单元效率排序研究：一种基于DEA的方法

王 庆, 郑彩玲, 刘学鹏

(1.天津商业大学 商学院，天津 300134; 2.天津商业大学 管理创新与评价研究中心，天津 300134)

统一组织管理下的单元效率排序研究：一种基于DEA的方法

王 庆1,2, 郑彩玲1, 刘学鹏1

(1.天津商业大学 商学院，天津 300134; 2.天津商业大学 管理创新与评价研究中心，天津 300134)

统一管理下，一个组织对其下属各个决策单元进行科学的效率评价和排序是其重要的运营管理活动之一。为了使得组织在统一的标准下对所有单元进行绩效排序，本文提出了一种新的基于公共权重的决策单元排序方法，该方法通过增加一个总和虚拟单元到评价系统，应用DEA方法求出使该虚拟单元效率最大的一组公共权重；同时提出第二个决策目标来解决权重不唯一问题，即基于公共权重所得效率与经典DEA方法所求的效率变化之和最小；然后基于所得公共权重对决策单元的绩效进行排序。最后，实例表明新的效率排序方法科学有效。

DEA；效率；排序；公共权重；总和虚拟单元

1 引言

管理领域、经济领域经常面临这样的问题：一个组织需要分析其多个相似子单元的相对效率，并进行排序。学者们提出了很多的效率评价和排序方法，其中数据包络分析(Data Envelopment Analysis, DEA)是被广泛运用的方法之一。DEA方法是一种非参数分析方法，由Charnes等[1]于1978年提出，用于评价有多个输入和多个输出的一组决策单元(DMU: Decision-Making Unit)的相对效率。虽然决策单元具体的生产函数形式并未确定，但每个决策单元的相对效率可表示为输出加权求和与输入加权求和的比。在DEA理论情境下，许多方法都用来对决策单元进行排序。现实中组织关注其下属决策单元效率的同时，也关注组织的总体消耗和产出，即关注组织的总体效率[2]。然而，学者们在对决策单元进行排序时，鲜有考虑到组织的总体效率最大化这一目标需求。因此，本文针对这一问题，提出了一个新颖的统一组织管理下的单元效率排序方法。该方法将组织视为一个整体，提出使组织的整体效率最大化来获取一组公共权重的DEA模型；提出第二决策目标，即基于公共权重所得效率与经典DEA方法所求的效率变化之和最小，从而获得唯一公共权重，实现客观稳定的单元排序。

2 相关研究评述

在DEA领域，对决策单元进行效率排序的方法大体可分为五类，它们具有各自的特点和特定的方案模型。第一类方法是基于公共权重进行效率排序的方法，如文献[3～5]，这类方法的特点是效率评价基于统一的公共权重准则，排序结果能被广泛接受，并且更符合人类的思维方式和行为习惯。第二类方法通过改变参照集得到效率排序结果，如文献[6～8]，这类方法的特点是丰富了效率评价的参照集，从而增强单元的效率区分，并且更客观。第三类方法是指通过改变目标函数(即排名标准)获得效率排序结果的方法，如文献[9～11]，这类方法的特点是根据不同的角度提出相应的排序准则，适合具体的排序需求。第四类方法是通过改变约束条件实现效率排序，如文献[12～16]，这类方法的特点是根据不同的角度构建问题求解的约束条件，满足单元评价和排序的不同需要。第五类方法是折中效率方法，如文献[17～22]，这类方法的特点是综合多种方法的排序结果，采用一定的折中策略进行单元综合排序，具有很好的兼顾性、协调性，能被各方所接受。必须指出，有些单元排序方法是综合各种思想而提出来的，这些方法在类属上具有交叉性，所以上述分类不是完全彼此独立、排他的，但这不会影响上述分类的可理解性、可行性和可操作性。

本文关注的是基于公共权重的方法进行统一组织管理下的单元效率评价和排序。经典DEA模型在评价个体单元的相对效率时，允许每个单元寻找到一组使得其自身效率最大化的权重。所以，经典DEA模型中不同单元之间因为权重的多样性，使得所获得的权重以及效率评价无法被广泛接受。尤其是在进行效率排序时，基于不同的权重的评价更不被大家所认可，因此寻找一组能被大多数决策单元所接受的公共权重，从而进行相对效率的评价和排序就显得较为重要。所以，单一公共权重是进行效率排序最显而易见的方法[23]。这种基于单一公共权重所进行的效率排序能确保所有单元在一个公平的环境下被评价比较[24]。

应用DEA方法求解公共权重最早由Cook和Kress于1990年在文献[25]中提出。随后，学者们继续围绕DEA情境下的公共权重求解问题进行不断的研究探索，提出各自的求解公共权重的方法。根据目标函数的不同，DEA情境下的公共权重求解方法可分为单目标求解方法和多目标求解方法。总的来说，单目标求解方法最为常见，大体上又可分为综合集成法和最小偏差(与理想参照点)法。综合集成法是指以最大化所有单元的效率之和或者效率平均值为目标求解公共权重，或者是以所有单元权重的平均值为公共权重的方法，这类方法综合了所有单元的诉求。综合集成法的代表文献包括如下3个。Ganley和Cubbin[26]提出了以最大化所有单元效率之和为目标求解公共权重的方法，从而排序决策单元。Roll和Golany[27]提出了两种公共权重求解方法：最大化所有单元的平均效率和最大化有效单元数量。Doyle[28]通过经典DEA模型求出不同单元的权重，然后取这些单元的对应权重的平均值构建成公共权重。最小偏差法是指以最小化所有单元与理想参照点(或最优前沿面)的效率(或距离)偏差为目标求解公共权重的方法，本质是使决策单元尽可能接近理想参照点。最小偏差法的代表文献相对较多，例如，Kao和Hung[29]提出以经典DEA模型所求单元的效率为理想效率值，最小化所求的效率与理想效率值偏差所求得权重为公共权重。Liu和Peng[30]提出以使得所有单元到前沿面的投影点之间的输入间隙和输出间隙距离之和最小为目标的求解公共权重方法，并最终进行效率排序。Cook和Zhu[31]构建了以所有决策单元与其理想效率水平之间(常规的DEA求得效率水平)差异的最大值最小化为目标的公共权重求解方法。与Cook和Zhu[31]相似，Hatefi和Torabi[32]通过最小化所有单元效率偏差(与1的差距)的最大值求解公共权重。Sun等[5]给出分别基于理想参照单元和非理想参照单元两个求解公共权重的模型，即分别以最小化所有单元与理想参照单元的距离和为目标，以最小化所有单元的最差效率和为目标。此外，Sinuany-Stern和Friedman[4]设计了DR/DEA模型，即利用线性判别分析法，求出有效和非有效决策单元占总决策单元的比例，以最大化判别标准(最大区分有效和非有效集)为目标求公共权重。相对于单目标方法，多目标方法的相关文献较少，例如，Jahanshahloo等[33]提出以所有单元的效率值同时最大化为目标的多目标规划求解公共权重，并最终进行效率排序。

必须指出，传统DEA所求的每个单元对应的权重存在不唯一的可能性[17]，这样许多基于DEA思想的方法所求的公共权重也就存在不唯一问题。Doyle和Green[17]认为引进第二目标函数是解决这个问题的有效办法，并提出了基于侵略策略和仁慈策略的两个交叉效率模型，以此获得唯一权重。随后，根据这个思路许多学者提出自己的求解唯一权重的办法。刘英平等[7]引入虚拟最优决策单元和虚拟最差决策单元，以最优决策单元的效率值最大、且最差决策单元的效率值最小为目标，求解唯一公共权重。Liang等[34]提出了3个基于第二目标的交叉效率模型，从而解决权重不唯一性的问题：最小化所有单元与理想点偏差的总和；最小化所有单元与理想点的最大偏差；最小化所有单元与理想点绝对偏差的平均值。

通过上述文献的回顾，可以看出在DEA情境下，着眼点不一样则会有不同的效率评价和排序方法，包括求解公共权重的方法也不一样。然而，极少有学者在对决策单元进行排序时，考虑到决策者对总体效率最大化这一需求。Lozano和Villa[35]提出通过改变传统DEA的目标函数，以最大化总虚拟单元的相对效率为目标求解公共权重，即所有单元的输入(输出)的平均值作为总虚拟单元的输入(输出)，从而解决资源分配问题。本文关注的是基于公共权重的方法进行统一组织管理下的单元效率评价和排序，即一方面关注组织的总体效率，同时兼顾考虑个体决策单元效率最大化。所以，借鉴Li和Cheng[2]，Lozano和Villa[35]视组织为整体的思想，本文提出使组织的整体效率最大化来获取一组公共权重。首先构建一个总和虚拟单元，其输入和输出分别为全部决策单元的总输入和总输出，并且将该虚拟单元增加到评价系统中使其成为待评价的一个决策单元。然后，为了解决公共权重不唯一性问题，提出第二个决策目标，即基于公共权重所得效率与经典DEA方法所求的效率变化之和最小，获得唯一公共权重实现全排序。

3 问题描述

本文关注的是统一组织管理下的单元绩效排序研究。在实践中许多组织经常面临这样的问题：需要分析其多个相似子单元的相对效率，并进行排序。例如，对于盈利型组织，一个企业集团需要考核在上一周期内它的子公司绩效状况并进行排序，然后根据排名状况进行奖惩；对于非盈利型组织，例如，政府需要考核在上一周期内它的所有公立学校绩效状况并进行排序，然后根据排名状况进行资源配置。所以无论是盈利型组织还是非盈利性组织，分析内部多个相似子单元的相对效率并进行排序的活动都普遍存在。经典DEA模型中不同单元之间因为权重的多样性，使得所获得的权重以及效率评价无法被广泛接受。因此寻找一组能被大多数决策单元所接受的统一公共权重，从而进行相对效率的评价和排序就显得较为重要。

本文研究的统一组织管理下的单元绩效排序问题具体界定为：一个组织有n个具有可比性的同类型决策单元(DMU)；每个决策单元DMUk(k=1,2,…,n)使用m种输入xik(i=1,2,…,m)，得到t种输出yrk(r=1,2,…,t)；vik和urk分别是决策单元DMUk第i个输入和第r个输出的权；DMUk的相对效率定义为输出加权求和与输入加权求和之比；寻找一组能被大多数决策单元所接受的公共权重，从而进行决策单元相对效率的评价和排序。

明确相关研究假定如下：

(1)对于整个组织，上个工作周期中各个子单元的输入数量和输出数量是已知的；

(2)对于每个单元，相对效率定义为输出加权求和与输入加权求和之比；

(3)效率评价排序是基于统一的公共权重，保证公平性；

(4)公共权重的选取由组织根据组织的总体效率而决定，不会由某个单元决定；

(5)公共权重的选取充分考虑组织的总体效率最大前提下，兼顾个体效率最大。

4 新的效率排序方法

假设一个组织有n个决策单元，每个决策单元有多个输入和多个输出，并且所有决策单元过去的绩效数据(包括输入和输出)已知。对于每个决策单元DMUj(j=1,2,…,n)，m个输入xij(i=1,2,…,m)产生t个输出yrj(r=1,2,…,t)。

然而从整体的角度来看，组织往往希望其自身总体效率达到最大。根据DEA理论，本文提出一种新的确定公共权重的方法：使组织总效率最大确定各个输入和输出的统一公平的权重。具体来说，视整个组织为一个总和虚拟单元DMUn+1，其相应的输入和输出可定义为

(1)

(2)

一定存在一组公共权重ur(r=1,…,t)和vi(i=1,…,m)，使得总和虚拟单元(即组织)的总体效率最大，具体见(3)式。

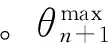
事实上，(3)式本质上是遵循传统DEA方法的原理，但是正如文献[16]所指出传统DEA方法获得权重往往具有不唯一性，容易造成单元效率评价的不稳定性。所以，解决公共权重不唯一性是本文必须研究的另外一个重要问题。考虑到这样的事实：对于每个决策单元，基于公共权重所得效率必然小于等于经典DEA方法所求的效率，这是由经典DEA原理决定的，并且每个决策单元总是希望自身效率最大化，即不期望两类效率的差距太大。所以，本文在(3)式的基础上，提出第二个决策目标来解决权重多样性这个问题，即基于公共权重所求得效率与经典DEA方法所求得效率变化之和最小，具体见模型(4)。

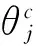
显然,(4)式降低了公共权重选取的不确定性,使得公共权重更加合理有效；并最终获得一组可以尽可能消除单元的权重偏好差异，最大程度地被所有单元接受的唯一公共权重ur(r=1,…,t)和vi(i=1,…,m)。根据这些公共权重，则第j个决策单元DMUj的效率值为

(5)

据此，对统一组织管理下的决策单元进行效率排序可分为如下四个步骤：

步骤1将组织视为一个总和虚拟单元DMUn+1，增加到评价系统中，其相应的输入和输出可由(1)式和(2)式获得。因此构建了一个含有n+1个决策单元的评价系统。

步骤2通过模型(3)、(4)，求出公共权重ur(r=1,…,t)和vi(i=1,…,m)。

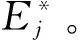
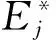
5 实例

为了便于示范，本文使用文献[35～37]已有的实例数据举例说明所提出的新排序方法科学性，该实例中包含10个决策单元，每个决策单元有2个输入和2个输出，具体数据见相关文献。首先将组织整体作为一个决策单元，增加到评价系统中，根据(3)、(4)式，求得公共权重(u1，u2，v1，v2)为(0.02431，0.01971，0.04928，0.04928)，该组权重尽可能消除单元的权重偏好差异，没有出现传统方法所形成的极端权重差异，易被所有单元接受。根据所得公共权重和(5)式，计算每个决策单元的效率，效率排序是(10，9，8，3，4，6，1，1，7，5)。而经典DEA模型CCR模型效率排序是(10，9，8，1，1，7，1，1，6，1)。比较发现，本文方法计算的决策单元的效率通常要小于或者等于用经典DEA模型所计算的效率，并且二者的差别基本不大，这是符合预期的。经典DEA模型计算得到的有效单元包括单元4、单元5、单元7、单元8、单元10，其它都为非有效单元，5个有效单元的效率排序并列为第一。用本文的方法能够对上述有效单元进行进一步效率区分和排序。具体来说，有效单元整体排名都靠前，单元7、单元8的效率排序并列第一；第三名到第五名分别是单元4、单元5、单元10。非有效单元整体排名都落后于有效单元，且非有效单元间的排序基本没有改变，只有单元6、单元9的排名顺序颠倒。综合来看，本文方法是基于一个公允、可广为接受的公共权重而进行的效率排序，结果符合实际，且更易被接受。

6 结论

决策单元效率排序是DEA范畴的非常重要的研究领域，基于统一的公共权重的效率排序方法是解决该领域问题最为广泛的方法之一。本文提出了一种新颖的基于公共权重的效率排序方法，与以往研究不同的是，该方法考虑到了组织的总体效率，提出了使组织的总体效率最大化为目标来求解公共权重；同时，提出基于公共权重所得效率与经典DEA方法所求的效率变化之和最小为第二个决策目标来解决公共权重不唯一性问题。实例应用表明，本文所提出的方法是一种具有综合性和妥协性的求解唯一公共权重方法，是科学有效的，能使效率排序效果更切合实际，更好满足决策者的需求。此外，本文的方法不仅适用于统一管理下组织对其下属决策单元进行科学的效率评价和排序，而且也适用于组织的资源、成本、收益的配置等领域。

[1] Charnes A, Cooper W W, Rhodes E. Measuring the efficiency of decision making units[J]. European Journal of Operational Research, 1978, 2(6): 429- 444.

[2] Li S, Cheng Y. Solving the puzzles of structural efficiency[J]. European Journal of Operational Research, 2007, 180(2): 713-722.

[3] Andersen P, Petersen N C. A procedure for ranking efficient units in data envelopment analysis[J]. Management Science, 1993, 39(10): 1261-1264.

[4] Sinuany-Stern Z, Friedman L. DEA and the discriminant analysis of ratios for ranking units[J]. European Journal of Operational Research, 1998, 111(3): 470- 478.

[5] Sun J, Wu J, Guo D. Performance ranking of units considering ideal and anti-ideal DMU with common weights[J]. Applied Mathematical Modelling, 2013, 37(9): 6301- 6310.

[6] Jahanshahloo G R, Afzalinejad M. A ranking method based on a full-inefficient frontier[J]. Applied Mathematical Modelling, 2006, 30(3): 248-260.

[7] 刘英平,林志贵,沈祖诒.有效区分决策单元的数据包络分析方法[J].系统工程理论和实践,2006,26(3):112-116.

[8] 毕功兵,陶成,梁樑,等.基于权重集合的决策单元排序方法[J].系统工程理论和实践,2010,30(12):37- 43.

[9] Obata T, Ishii H. A method for discriminating efficient candidates with ranked voting data[J]. European Journal of Operational Research, 2003, 151(1): 233-237.

[10] Jahanshahloo G R, Hosseinzadeh L F, Rezaie V, et al.. Ranking DMUs by ideal points with interval data in DEA[J]. Applied Mathematical Modelling, 2011, 35(1): 218-229.

[11] Guo D, Wu J. A complete ranking of DMUs with undesirable outputs using restrictions in DEA models[J]. Mathematical and Computer Modelling, 2013, 58(5- 6): 1102-1109.

[12] Mehrabian S, Alirezaei M R, Jahanshahloo G R. A complete efficiency ranking of decision making units[J]. Computational Optimization and Applications, 1999, 14(2): 261-266.

[13] Saati S, Zarafat M, Memariani A, et al.. A model for ranking decision making units in data envelopment analysis[J]. Ricerca Operativa, 2001, 31(97): 47-59.

[14] Chen Y. Measuring super-efficiency in DEA in the presence of infeasibility[J]. European Journal of Operational Research, 2005, 161(2): 545-551.

[15] Li X B, Reeves G R. A multiple criteria approach to data envelopment analysis[J]. European Journal of Operational Research, 1999, 115(3): 507-517.

[17] Doyle J, Green R. Efficiency and cross-efficiency in DEA: derivations, meanings and uses[J]. Journal of the Operational Research Society, 1994, 45(5): 567-578.

[18] Liang L, Wu J, Cook W D, et al.. Alternative secondary goals in DEA cross-efficiency evaluation[J]. International Journal of Production Economics, 2008, 113(2): 1025-1030.

[19] Zerafat A M, Mustafa A, Kamali M J. Cross-ranking of decision making units in data envelopment analysis[J]. Applied Mathematical Modelling, 2013, 37(1-2): 398- 405.

[20] Khodabakhshi M, Aryavash K. Ranking all units in data envelopment analysis[J]. Applied Mathematics Letters, 2012, 25(12): 2066-2070.

[21] 薛声家,王清.基于超效率模型的决策单元区间效率值排序[J].暨南大学学报(自然科学版),2011,32(5):447- 450.

[22] 王美强,梁樑.CCR模型中决策单元的区间效率值及其排序[J].系统工程,2008,26(4):109-112.

[23] Adler N, Friedman L, Sinuany-Stern Z. Review of ranking methods in the data envelopment analysis context[J]. European Journal of Operational Research, 2002, 140(2): 249-265.

[24] Karsak E E, Ahiska S S. Practical common weight multi-criteria decision-making approach with an improved discriminating power for technology selection[J]. International Journal of Production Research, 2005, 43(8): 1537-1554.

[25] Cook W D, Kress M. A data envelopment model for aggregating preference ranking[J]. Management Science, 1990, 36(11): 1302-1310.

[26] Ganley J A, Cubbin J S. Public sector efficiency measurement: applications of data envelopment analysis[M]. Amsterdam: North-Holland, 1992.

[27] Roll Y, Golany B. Alternate methods of treating factor weights in DEA[J]. Omega, 1993, 21(1): 99-109.

[28] Doyle J R. Multiattribute choice for the lazy decision maker: let the iternatives decide[J]. Organizational Behavior and Human Decision Processes, 1995, 62(1): 87-100.

[29] Kao C, Hung H T. Data envelopment analysis with common weights: the compromise solution approach[J]. The Journal of the Operational Research, 2005, 56(10): 1196-1203.

[30] Liu F F, Peng H H. Ranking of units on the DEA frontier with common weights[J]. Computers & Operations Research, 2008, 35(5): 1624-1637.

[31] Cook W D, Zhu J. Within-group common weights in DEA: an analysis of power plant efficiency[J]. European Journal of Operational Research, 2007, 178(1): 207-216.

[32] Hatefi S M, Torabi S A. A common weight MCDA-DEA approach to construct composite indicators[J]. Ecological Economics, 2010, 70(1): 114-120.

[33] Jahanshahloo G R , Memariani A, Hosseinzadeh L F, et al.. A note on some of DEA models and finding efficiency and complete ranking using common set of weights[J]. Applied Mathematics and Computation, 2005, 166(2): 265-281.

[34] Liang L, Wu J, Cook W D, et al.. Alternative secondary goals in DEA cross-efficiency evaluation[J]. International Journal of Production Economics, 2008, 113(2): 1025-1030.

[35] Lozano S, Villa G. Centralized resource allocation using data envelopment analysis[J]. Journal of Productivity Analysis, 2004, 22(1-2): 143-161.

[36] Golany B, Phillips F Y, Rousseau J J. Models for improved effectiveness based on DEA efficiency results[J]. IIE Transactions, 1993, 25(6): 2-10.

[37] Beasley J E. Allocating fixed costs and resources via data envelopment analysis[J]. European Journal of Operational Research, 2003, 147(1): 198-216.

Ranking Efficiency of Units under a Central Organization:A Modified DEA Method

WANG Qing1,2, ZHENG Cai-ling1, LIU Xue-peng1

(1.SchoolofBusiness,TianjinUniversityofCommerce,Tianjin300134,China; 2.ManagementInnovationandEvaluationResearchCenter,TianjinUniversityofCommerce,Tianjin300134,China)

Under the management of a central organization, evaluating and ranking the efficiency of each division or subsidiary is an important activity. In order to rank all the DMUs on the same scale, this paper proposes a new method to determine the common weight based on DEA theory. We introduce total virtual unit to DMUs system and make its efficiency maximum to identify a common set of weights for all the DMUs. Meanwhile, to keep the weights uniqueness, it puts forward to the second goal which is to minimize the sum of the deviation between the efficiency based on the common weights and the efficiency based on the classic DEA for all the DMUs. An example is given to prove the effectiveness of our new evaluation method at last in this paper.

data envelopment analysis; efficiency; rank; common weights; total virtual unit

2014- 07- 07

国家自然科学基金资助项目(71401123)；天津市哲学社会科学规划基金资助项目(TJGL12- 041)

C934

A

1003-5192(2015)03- 0065- 05

10.11847/fj.34.3.65