解释变量内生假定下非参数空间计量模型的局部线性工具变量估计
冯 烽
(1.清华大学 经济管理学院,北京 100084; 2.广西财经学院 信息与统计学院,广西 南宁 530003)
解释变量内生假定下非参数空间计量模型的局部线性工具变量估计
冯 烽1,2
(1.清华大学 经济管理学院,北京 100084; 2.广西财经学院 信息与统计学院,广西 南宁 530003)
为刻画解释变量的空间外溢效应与变量间的非线性关系,本文提出了一种非参数空间计量模型,并给出了模型含内生变量情况下的局部线性工具变量估计。该估计方法最大的优点是可以同时获得偏导数的估计,便于进行经济学的边际分析。数值模拟结果表明,局部线性工具变量估计优于核估计。中国地区R&D要素外溢效应的实证结果显示,周边地区R&D内部经费支出对本地区R&D产出具有非线性的正向影响,且周边地区R&D内部经费支出的边际产出存在空间集聚现象,实证结论显示了非参数空间计量模型的适用性与合理性。
非参数;空间计量;内生;局部线性工具变量估计
1 引言
近年来,空间计量模型因打破了个体相互独立的传统计量模型假定,其理论与应用研究引起了国内外学者的持续关注。Kelejian和Prucha[1]研究了空间自回归(SAR)模型的广义矩估计及其大样本性质;Lee[2]与Kelejian等[3]分别给出了误差空间相关的空间自回归(SARAR)模型的两阶段最小二乘估计与工具变量估计;Elhorst[4]考察了空间面板数据模型的估计与识别问题,随后,Elhorst[5]推导了误差空间自相关的固定效应动态面板数据模型的极大似然估计及其性质;Su和Yang[6]在Elhorst[5]的基础上,针对固定效应与随机效应两种情形,给出了误差空间自相关动态面板数据模型的拟极大似然估计;Lee和Yu[7]则在Elhorst[5]的基础上考察了更一般的空间动态面板数据固定效应模型及其极大似然估计;郭鹏辉[8]在Lee和Yu[7]的基础上研究了内生初始假定下空间动态固定效应模型的拟极大似然估计;魏传华和梅长林[9]针对半参数空间变系数回归模型给出了后向拟合估计;José-María等[10]给出了一种带有非参数空间趋势的SAR模型并提出了模型的P样条估计方法;冯烽和叶阿忠[11]提出了一种半参数面板数据模型并应用于中国EKC假说的实证研究。
纵观已有研究,参数形式的空间计量模型及其理论研究已取得了很大的进展,然而,有关非参数空间计量模型的研究并不多见。由于经济系统中变量之间的关系并非总是线性关系,此时主观设定计量模型变量间的参数关系将会造成模型设定及参数估计的偏误。为此,本文提出一种含内生解释变量的非参数空间计量模型并给出其局部线性工具变量估计,该估计不仅具有良好的渐近性质,还可以估计出经济学边际分析中被解释变量关于解释变量的偏导数。
2 模型的建立
本文将解释变量的空间滞后项引入传统的非参数计量模型,旨在同时刻画解释变量的空间外溢效应与变量间可能的非线性关系。考察如下的横截面数据非参数空间计量模型
(1)
其中xi∈Rq为解释变量列向量个体i的观测值,x1,…,xn相互独立,T为转置算子,ωi=(ωi1,…,ωin)为根据个体i与其它个体之间的距离而定义的空间权重行向量,X=(x1,…,xn)T为n×q的矩阵,G(·)为未知函数,yi∈R为被解释变量,ui为随机扰动项,n为个体的数目。
(1)式所表示的非参数空间计量模型的含义是:地区i的被解释变量不仅受其自身因素的影响,同时还受到周边地区相应因素的影响,因此,这类模型具有广泛的现实意义。例如,一个地区物流业的发展水平既受到本地区交通运输发展状况的影响,同时还受到邻近地区交通运输发展状况的影响;再如,某地区某天的降雨量可以认为是本地区气候条件以及邻近地区气候条件共同作用的结果。
3 非参数空间计量模型的局部线性工具变量估计
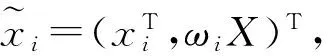
(2)
为推导估计量,本文作如下假设:
假设1G(·) 及其一阶、二阶导数连续且有界。

假设1是使得G(·)能够进行一阶Taylor展开,且根据Stone[12]可得非参数函数G(·)估计的最优收敛速度为n-2/(2q+5);假设 2 是根据工具变量的定义要求工具变量必须与随机扰动项不相关。对于参数形式的空间计量模型的工具变量估计,Kelejian等[3]建议取解释变量的空间滞后项(或高阶空间滞后)作为工具变量;对于本文所提出的非参数计量模型的局部线性工具变量估计,可以取解释变量的空间滞后项(或高阶空间滞后)作为工具变量,还可以从经济系统外寻找合适的工具变量。
(3)

结合(2)式与(3)式得
(4)
(5)

(6)
将(6)式用矩阵的形式表示如下
(7)
其中Z=(Z1,Z2,…,Zn)
假设3矩阵ZWxXx可逆。
在假设3下,由(7)式可得
(8)
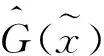
即有
(9)
其中e1=(1,0,…,0)T为2q+1维列向量。
4 Monte-Carlo模拟与实证分析
4.1 Monte-Carlo模拟
为避免非参数估计中的“维数诅咒”问题,仅考察xi为一维内生变量的情形。假设随机扰动项ui(i=1,…,n)独立且服从[-0.5,0.5]上的均匀分布,取内生变量xi=exp(0.5ui),被解释变量的生成过程为yi=4sinxi+(ωiX)2+ui,其中X=(x1,…,xn)T,取空间邻接矩阵为Rook相邻型空间权重矩阵,ωi为空间权重矩阵的第i行,空间单元个数n分别取25、64、100、225、400进行模拟,局部线性工具变量估计(LLIVE)与核估计(KE)[14]结果的均方误如下
其中右下方数值和括号内数值分别是相应的样本量和选取的最优窗宽。
各样本量下采用局部线性工具变量估计的均方误均小于核估计的均方误,即从拟合的效果看,局部线性工具变量估计优于核估计;且局部线性工具变量估计的均方误基本上随样本量的增加而减少,这一结果支持了局部线性工具变量估计的渐近正态性。
4.2 实证案例分析
为验证模型的合理性与适用性,构建非参数空间计量模型对中国R&D要素投入的空间外溢效应进行实证研究。为避免维数过高引致收敛慢的问题,仅考虑一种要素投入及其溢出效应,本文的局部线性工具变量估计恰好能够有效解决由于遗漏变量所可能产生内生性问题。模型设定如下
yi=G(rdi,ωird)+ui
(10)
其中rdi为地区i的R&D内部经费支出,rd=(rd1,…,rd31)T,ωi为地区i与各地区Rook型邻接情况的权重行向量,yi为地区i的R&D产出,由地区i的三种专利申请量表示。为避免窗宽过大,对被解释变量与解释变量均取人均值,数据来源于中国科技统计年鉴(2012)、中国统计年鉴(2012)。该模型既可以反映技术创新中的研发溢出现象[15],还可以刻画投入产出复杂系统的非线性关系。
局部线性工具变量估计的MSE最小,OLS次之,核估计的MSE最大,这表明在该实证案例中局部线性工具变量估计优于其他两种估计方法。根据实证结果,并结合中国R&D的地区差异状况,分析如下:
(1)中国R&D内部经费支出具有空间外溢效应,即本地区的专利申请量不仅与本地区R&D内部经费支出有关,还受到周边地区R&D内部经费支出的影响。这是因为y关于rd与ωrd的偏导数的估计结果均为正值表明本地区R&D内部经费支出的增加以及周边地区R&D内部经费支出的增加均能促进本地区R&D的产出。
(2)本地区R&D内部经费支出与周边地区R&D内部经费支出对本地区R&D产出的作用机制不同,其中本地区R&D内部经费对本地区R&D产出的影响是线性的,但周边地区R&D内部经费支出对本地区R&D产出的影响却是非线性的。这是因为本地区R&D内部经费的边际产出∂y/∂(rd)的地区差异不大,这与线性模型中rd系数的p值小于5%一致,而周边地区R&D内部经费对本地区的边际产出∂y/∂(ωrd)却存在较大的地区差异,线性模型中ωird系数的p值大于5%也支持了这一结论。
(3)周边地区R&D内部经费支出对本地区R&D的边际产出存在空间集聚现象。其中天津、辽宁、上海、江苏、浙江、福建、山东等东部沿海省份对周边地区R&D内部经费的转化能力较高;贵州、云南、西藏、甘肃、青海等西部地区对周边地区R&D内部经费的转化能力则较低。
5 研究结论
本文构建的非参数空间计量模型结合了空间计量模型与非参数模型的优点,针对模型所给出的局部线性工具变量估计具有良好的渐近性质和经济意义,并且能够有效避免变量的内生性问题,数值模拟结果表明局部线性工具变量估计优于核估计,对中国地区R&D投入产出的实证计量研究验证了本文模型的适用性与合理性。
[1] Kelejian H H, Prucha I R. A generalized moments estimator for the autoregressive parameter in a spatial model[J]. International Economic Review, 1999, 40(2): 509-533.
[2] Lee L F. Best spatial two stage least squares estimators for a spatial autoregressive model with autoregressive disturbances[J]. Econometric Reviews, 2003, 22: 307-335.
[3] Kelejian H H, Prucha I R, Yuzefovich E. Instrumental variable estimation of a spatial autoregressive model with autoregressive disturbances: large and small sample results. Advances in Econometrics: Spatial and Spatiotemporal Econometrics[M]. New York: Elsevier Ltd, 2004. 163-198.
[4] Elhorst J P. Specication and estimation of spatial panel data models[J]. International Regional Science Review, 2003, 26: 244-268.
[5] ElhorstJ P. Unconditional maximum likelihood estimation of linear and log-linear dynamic model for spatial panels[J]. Geographical Analysis, 2005, 37: 85-106.
[6] SuL J, Yang Z L. QML estimation of dynamic panel data models with spatial errors[D]. Singapore Management University, 2007.
[7] Lee L F, Yu J. Some recent developments in spatial panel data models[J]. Regional Science and Urban Economics, 2010, 40(5): 255-271.
[8] 郭鹏辉.内生初始假定下动态空间固定效应模型的拟极大似然估计[J].统计研究,2011,28(10):103-110.
[9] 魏传华,梅长林.半参数空间变系数回归模型的Back-Fitting估计[J].数学的实践与认识,2006,36(3):177-184.
[10] José-María M, Román M, María D. SAR models with nonparametric spatial trends. a p-spline approach[J]. Estadística Espaola, 2012, 54: 89-111.
[11] 冯烽,叶阿忠.中国的碳排放与经济增长满足EKC假说吗——基于半参数面板数据模型的检验[J].预测,2013,32(3):59- 66.
[12] Stone C J. Optimal global rates of convergence for nonparametric regression[J]. The Anals of Statistics,1982,10: 1040-1053.
[13] 叶阿忠.非参数和半参数计量经济模型理论[M].北京:科学出版社,2008.
[14] Nadaraya E A. On estimating regression[J]. Theory of Probability and Its Applications,1964, 10: 186-196.
[15] 吴玉鸣,何建坤.研发溢出、区域创新集群的空间计量经济分析[J].管理科学学报,2008,11(4):59- 66.
Local Linear Instrumental Variable Estimation of a Nonparametric Spatial Model Under Endogenous Explanatory Variable Assumption
FENG Feng1,2
(1.SchoolofEconomicsandManagement,TsinghuaUniversity,Beijing100084,China; 2.SchoolofInformationandStatistics,GuangxiUniversityofFinanceandEconomics,Nanning530003,China)
This paper proposes a nonparametric spatial model to capture the spatial spillover effect of explanatory variable and the nonlinear relationship in variables, as well as proposes a local linear instrumental variable estimation for the nonparametric spatial model with endogenous explanatory variable. As an advantage of this estimation method, it can estimate the partial derivative, which facilitates marginal analysis in economics. The numerical simulation results show that local linear instrumental variable estimation is superior to kernel estimation. The empirical results of R&D element spillover effect show that R&D intramural expenditure of neighborhood regions has a nonlinear positive influence on R&D output, and the marginal output of R&D intramural expenditure from neighborhood regions appears spatial agglomeration phenomenon. The empirical results also validate the applicability and rationality of the nonparametric spatial model.
nonparametric; spatial econometrics; endogenous; local linear instrumental variable estimation
2014- 06- 03
国家自然科学基金资助项目(71171057);广西自然科学基金资助项目(2014GXNSFBA118011);广西高校科研资助项目(ZD2014120);广西数量经济学重点学科开放性课题(2014YBKT01);广西高校数理金融高水平创新团队及卓越学者计划资助项目(2014CXTD17)
O212
A
1003-5192(2015)03- 0057- 04
10.11847/fj.34.3.57
——基于Gini 系数和Theil 指数的测算

