一组最值难题“圆”来如此容易

☉江苏省南京市金陵中学河西分校 李玉荣

一组最值难题“圆”来如此容易

☉江苏省南京市金陵中学河西分校 李玉荣

引例（义务教育教科书苏科版《数学》九年级（上册）第154第16题）如图1，P是⊙O外的一点，直线PO分别交⊙O于点A、B，则PA是点P到⊙O上的点的最短距离，PB是点P到⊙O上的点的最长距离，你能说明理由吗？

证明：如图1，在⊙O是任取一点C（不为A、B），连接PC，OC.

因为PO＜PC+OC，PO=PA+OA=PA+OC，所以PA＜PC，即PA是点P到⊙O上的点的最短距离.

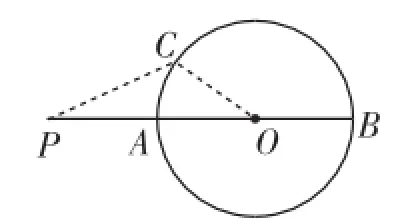
图1

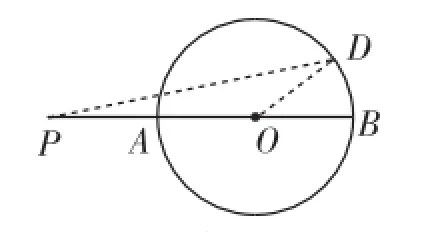
图2

如图2，在⊙O是任取一点D（不为A、B），连接PD，OD.

因为PO+OD＞PD，PB=PO+OB=PO+OD，所以PB＞PD，即PB是点P到⊙O上的点的最长距离.

研读引例，笔者发现当点P在圆内时结论也成立，这些结论可以巧妙地用来解决一些最值问题，下面采撷几例中考题，剖析解法，以飨读者.

一、 动点在已知圆外

例1（2014年无锡）如图3，菱形ABCD中，∠A=60°，AB=3，⊙A、⊙B的半径分别为2和1，P、E、F分别是边CD、⊙A和⊙B的动点，则PE+PF的最小值是________.

图4

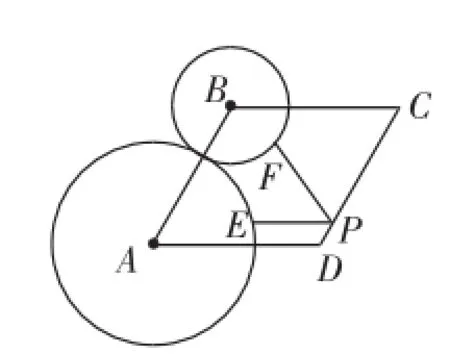
图3

解析：先将点P固定在AC的一个位置，连接PA、PB交⊙A和⊙B于点E、F，根据引例知此时“PE+PF的值最小值”，从而只需求“PA+PB的最小值”，而A、B是定点，P是CD上的动点，可用对称法求解.如图4，作点A关于CD的对称点A′，连接A′B，交直线CD于点P，则点P与D重合，PA+PB的最小值就是A′B的长，易知∠BAA′=90°，∠A′= 30°，所以A′B=2AB=6，即PA+PB的最小值为6，于是PE+ PF的最小值为6-3=3.

评注：此题有三个动点，难度较大，先假定点P固定，P在⊙A、⊙B上，P为圆外的一点，根据引例知，当E、F分别是PA、PB与⊙A、⊙B的交点时，PE+PF最小，再利用对称法求解.

二、 动点是斜边为定值的直角三角形的直角顶点

图5

例2（2013年武汉）如图5，E、F是正方形ABCD的边AD上两个动点，满足AE=DF.连接CF交BD于点G，连接BE交AG于点H.若正方形的边长为2，则线段DH长度的最小值是__________.

解析：点D为定点，H为动点，易证∠DAG=∠DCG，∠DCG=∠ABE，所以∠AHB=90°，故点H在以AB为直径的圆上.

评注：此题难度很大，先利用全等三角形证明∠AHB=90°，发现点H是斜边为AB=2的直角三角形的直角顶点，联想到以AB为直径的圆，D是⊙O外一定点，根据引例知H为OD与⊙O的交点时DH最小，从而得解.

三、 动点到一个定点的距离为定值

例3（2014年成都）如图6，在边长为2的菱形ABCD中，∠A=60°，M是AD边的中点，N是AB边上一动点，将△AMN沿MN所在的直线翻折得到△A′MN，连接A′C，则A′C长度的最小值是_______.

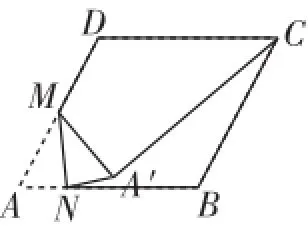
图6

图7

解析：因为MA′=MA=l，M为定点，所以点A′在以M为圆心，半径为1的⊙M上，连接MC与⊙M交于点A′，如图7，根据引例知此时A′C的长度最小.

过点M作MF⊥DC于点F，

在边长为2的菱形ABCD中，∠A=60°，

所以CD=2，∠ADC=120°，

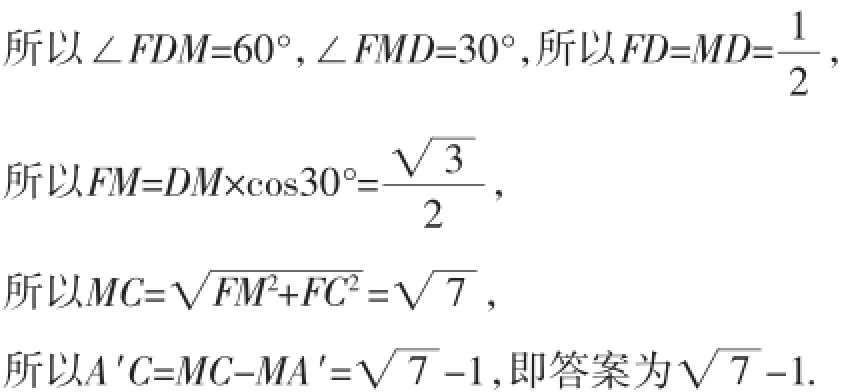
评注：此题动点A′到定点M的距离等于AM=1，为定长，联想到以M为圆心、半径为1的圆，C是⊙M外一定点，根据引例知A′为CM与⊙M的交点时A′C的长度最小，从而得解.

例4（2012年济南）如图8，在Rt△ABC中，∠ACB=90°，∠A=30°，AC=BC的中点为D，将ABC绕点C顺时针旋转任意一个角度得到△FEC，EF的中点为G，连接DG，在旋转过程中，DG的最大值为（）.

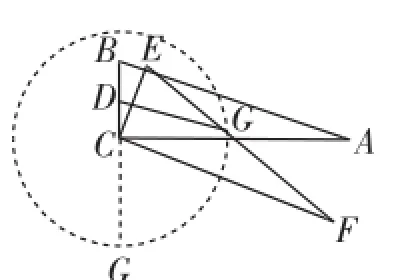
图8

所以点G在以C为圆心，半径为4的⊙C上.

延长BC交⊙C于点G，根据引例知此时DG最大，DG的最大值=DC+CG=6，所以选B.

评注：此题动点G到定点C的距离为定长4，联想到以C为圆心、半径为4的圆，D为⊙C内一个定点，根据引例知G是射线DC与⊙C的交点时DG最大，从而得解.

例5（2012年义乌）在锐角△ABC中，AB=4，BC=5，∠ACB=45°，将△ABC绕点B按逆时针方向旋转，得到△A1BC1.

（1）如图9，当点C1在线段CA的延长线上时，求∠CC1A1的度数；

（2）如图10，连接AA1，CC1，若△ABA1的面积为4，求△CBC1的面积；

（3）如图11，点E为线段AB的中点，点P是线段AC上的动点，在△ABC绕点B按逆时针方向旋转过程中，点P的对应点是点P1，求线段EP1长度的最大值与最小值.

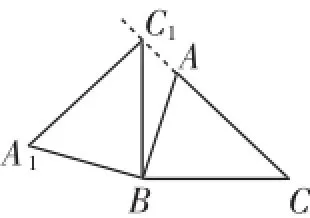
图9

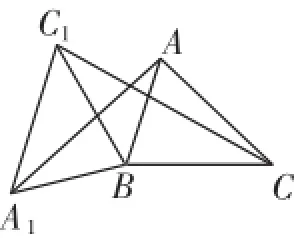
图10

图11

解析：（1）、（2）略.

（3）点P是线段AC上的动点，同时还绕点B按逆时针方向旋转，不妨以“退”求进，先将点P固定在AC的一个位置，其对应点P1在以B为圆心、BP为半径的⊙B上，延长BA、AB分别交⊙B于点P1，P1′，根据引例知此时EP1′最大、EP1最小，而BE=2，只需先求BP1的最大值和最小值：当BP1⊥AC时，小，此时EP1长度的最小值点P1与点C重合时，BP1=BC=5最大，此时EP1长度的最大值为5+2=7.

评注：此题难度很大，先将P固定在AC的一个位置，联想到以B为圆心、BP为半径的⊙B，E为⊙B内一个定点，根据引例知P是直线BE与⊙C的交点时，得到要想求线段EP1长度的最大值与最小值，只需求BP的最大值与最小值，问题不难得解.

义务教育《数学课程标准》（2011年版）指出：“数学活动经验的积累是提高学生数学素养的重要标志，教学中注重结合具体的教学内容，设计有效的数学探究活动，使学生经历数学的发生发展过程，是学生积累数学活动经验的重要途径.”上述几道中考最值问题颇有难度，构造辅助圆将所求最值问题转化为引例的模型，求解变得十分顺畅，有助于学生初步形成“模型思想”、积累数学活动经验，让人不由感叹：破解最值难题，“圆”来如此容易！H