对一个将军饮马模型问题的三个反思

☉甘肃省天水市第七中学 吴俊杰

对一个将军饮马模型问题的三个反思

☉甘肃省天水市第七中学 吴俊杰

题目（2013年苏州数学中考）如图1，在平面直角坐标系中，Rt△OAB的直角顶点A在x轴的正半轴上.顶为斜边OB上的一个动点，则PA+PC的最小值为_______.

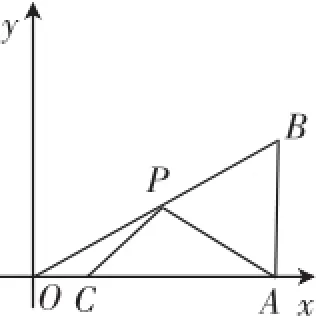
图1

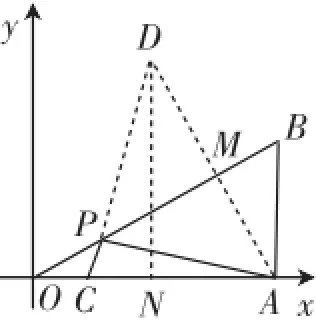
图2

参考答案：如图2，作点A关于OB的对称点D，连接CD交OB于点P，连接AP，过点D作DN⊥OA于点N，则此时PA+PC的值最小.因为B（3，），所以AB=OA=3，∠B=60°，由勾股定理得OB=2，由三角形面积公式因为∠AMB=∠BAO=90°，∠B=60°，所以∠BAM=30°，∠OAM=60°.因为DN⊥OA，所以∠NDA=由勾股定理得Rt△DNC中，由勾

反思1：为何舍弃另一种思路？

此题属于典型的“将军饮马”问题，在尺规作图问题中有两种解答思路：（1）作点A关于直线OB的对称点D，连接CD与直线OB相交于点P；（2）作点C关于直线OB的对称点E，连接AE与直线OB相交于点P.两种方法的本质是相同的，思路也是相同的，只是选择的点不同罢了，而且两种作图方法最终确定的点P的位置是重合的，PA+ PC的最小值即线段CD或线段AE的长也被唯一确定.因此，在日常教学中没有引起学生和教师的足够注意，思路（1）或思路（2）的选择随意性很大，没有任何甄选的过程.

那么，在具体问题解答中，应该选择作点A还是选择作点C的对称点呢？还是两种选择都是一样的呢？

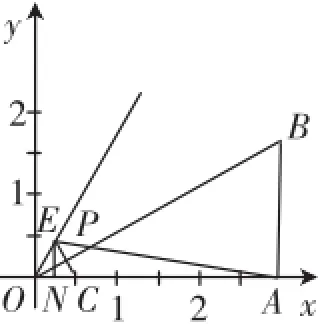
图3

本题参考答案选择“作点A关于OB的对称点D，连接CD交OB于点P”，如图2，给出了解答，通过网络搜索发现许多文献也直接借鉴了这一解法.那么为什么选择思路（1），而不选择思路（2），是因为思路（2）复杂吗？还是因为两种思路本质相同选择哪一个对于问题的解决没有影响？下面先给出基于思路（2）的证明：如图3，作点C关于直线OB的对称点E，连接AE与直线OB相交于点P.过点E作EN⊥OA，垂足为N.因为

对比两种方法，可以发现思路（2）较参考答案更简捷，涉及的知识点和要求更少，推理难度更低.分析解题方案选择中厚此薄彼的原因，可能在于解题者受“将军饮马”问题尺规作图方法的影响，认为两种思路的效果是一样的，因而在问题被迁移到本题中的时候，也武断地认为选择哪种思路解答都没有区别，就选择了作点A的对称点.讨论中另有教师指出，或许因为点A距离OB较远，且点A是直角三角形的顶点位置较为特殊，作出的图形更显大气，不似图3中各图形元素聚集在小范围内显的拥挤繁杂，而有时候繁杂的图形会影响解题人的思路，且不利于分析相互间的关系.此言也并非没有道理，但笔者认为，此解中“厚此薄彼”暴露出解题人在问题解答中缺少对各种解题思路的一种“先行预判”和“甄选”，即在选择作点A和点C的对称点两种思路之间缺乏对解答中可能用的知识点、方法，以及难易程度、可行性等缺乏比较分析，以至于解题分析中方案的选择更多的表现为一种随意性.

反思2：问题可否推广到一般情况？

事实上，也可以同时作出点A和点C关于OB的对称点，如图4，根据轴对称性可以发现，在原题已知条件下可以发现O、D、E三点在同一条直线上，△OAD是等边三角形，并且△DOC≌△AOE，其中OD=OA，OE=OC，∠DOA=∠EOC=2∠BOA=60°，可以得到四边形ADEC是等腰梯形等结论，对角线CD和AE的长度都等于PA+PC的最短距离.基于这一认识，我们可以继续考虑问题的一般形式.

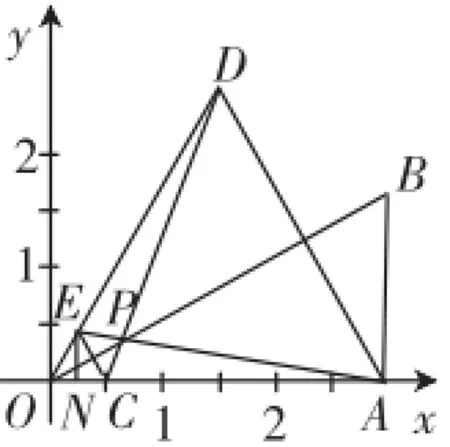
图4

图5

对于一般情况有：点A、C是直线m同侧的两个点，设直线AC（记作直线n）与直线m相交于点O，且夹角记作θ，如图5，作出点A、C关于直线m的对称点D、E，根据对称性可以确定O、D、E三点依然在同一条直线上，且∠DOA=2∠BOA=2θ，记OC=OE=b，OA=OD=a，在△AOE中，由余弦定理可知AE2=OE2+OA2-2OE·OA·cos∠DOC= OC2+OA2-2OC·OA·cos2∠BOA=b2+a2-2abcos2θ.所以PA+

如果要回避余弦定理，利用三角函数和勾股定理也可求得AE的长.根据图3也可以得到上述结论，但是参考答案（如图2）的方法就显得无能为力了，因为它没有把将军饮马问题中的三个决定因素有效聚集在一起，尤其没有有效聚集在同一个三角形中，从这个角度分析，可以再一次发现参考答案舍弃思路（2）的遗憾.

至于它的应用不再举例，因为分析上面一般形式，不是为了总结什么公式或者新定理以求直接在解答问题的时候套用，而是希望通过探究，使得将军饮马模型问题中决定最短距离的三个参数a、b、θ（即OC、OA、直线m和直线n的夹角）在确定最短距离中的作用，进一步说明参考答案舍弃思路（2）的不智.再者，利用这一结论可以将几何问题化归为代数问题求解，体现了化归思想，且在实际生产、工程问题中代数方法应用更为广泛和更有应用价值.

反思3：在实际生活中，将军饮马模型问题还有哪种参数系统？

在前面分析中，指出线段OC、线段OA、直线m和直线n的夹角是决定PA+PC的最短距离的三个参数，那么在实际生活中，还有没有其他的决定最短距离的参数系统？

略作分析，可以发现在实际生活中，还可以确定另外一种确定最短距离的参数系统，即点C到直线m的距离CM，记作h1，点A到直线m的距离AN，记作h2，以及点A和点C之间的距离，记作d，这三个参数都是实际生活中比较容易测量的.如图6，前面已经分析过，四边形ACED是等腰梯形，最短距离为对角线AE或CD，过点C、D分别向AD作垂线，垂足为F、G，根据等腰梯形的性质可得AF= h2-h1，DF=2h2-（h2-h1）=h2+h1，由勾股定理可得CD2=CF2+ DF2，AC2=CF2+AF2，消去CF2可得CD2=AC2-AF2+DF2=d2-（h2-h1）2-（h2+h1）2，所以PA+PC的最短距离为

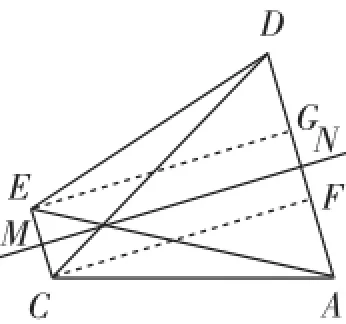
图6

下面这道源自百度百科的问题，可以很好地说明第二种参数系统在生活中的应用价值.如图7，有A、B两个村庄，他们想在河流m的岸边建立一个水泵站，已知每米的管道费用是100元，测量得到A到河流的距离AD是1km，B到河流的距离BE是3km，DE长3km.请问这个水泵站应该建立在哪里使得费用最少？为多少？

分析：问题中告知村庄A、B到河流岸边的距离，在实际生活中这也是比较容易测量的量.在第二套参数系统中，可以很容易由AD、BE、AB确定DE.如图7所作，C点为水泵站的位置，所铺设的水管长度就是AC+BC=A′C+ BC=A′B.因为EF=A′D=AD=1km，所以BF=BE+EF=4km.又A′F=DE=3km，在Rt△A′BF中，A′B2=A′F2+BF2，解得A′B=5km.所以总费用为500000元.

至此，我们得到了将军饮马模型问题的两种参数系统，虽然涉及参数系统不同时表达式不同，但其本质是相同的.从图5、图6的分析也暴露出原试题参考答案贸然舍弃“过点C作关于直线OB的对称点”的不妥.这就启发我们，在选择解题思路的时候，一定要有问一问“为什么要这样，而不能那样”，要有一个“先行预判”和“甄选”的过程.H

图7