刍议“解题能力”在初中数学中的培养与探索

☉江苏省泰州市田河初级中学 徐玲

刍议“解题能力”在初中数学中的培养与探索

☉江苏省泰州市田河初级中学 徐玲

“解题能力”的提高是人们认识世界、改造世界的关键，《中学数学新课程标准》中明确提出对学生“解题能力”的培养，学生在不断解决问题的过程中，掌握方法、领悟思想，学习科学严谨的思维方法，以扩展学生思维的广阔性、深刻性、敏捷性和批判性，以使学生形成良好的思维品质.

一、“隐含”条件在解题中的挖掘，整合信息提高思维意识

1.从已知条件中挖掘隐含条件，顺向推理

顺向推理是指学生从已知出发，逐步到达未知，这是解决问题的一般方法.

案例1：已知m、n都为质数，且满足3m+5n=31，试求

隐含条件挖掘：由题意可知m、n是质数，31为奇数，学生联想到3m与5n之中必然有一个为奇数、一个为偶数，从而找到解决问题的方法.

解析：对3m和5n进行讨论.

（1）若3m为奇数，则5n一定为偶数，奇数和偶数相乘仍然为偶数，可以得出n=2，解方程得m=7，代入可得

（2）若5n为奇数，则3m为偶数，即m=2，解方程得n= 5，代入可

通过对已知条件的思考，挖掘出了其中的隐含条件，进行讨论，顺利实现了问题的解决.

2.从未知结论中挖掘隐含条件，逆向推理

逆向推理是指学生从问题出发，根据问题的需要选择数学公式、定律和推论，从而实现问题的解决.

通过对结果的分析，使得学生想要将已知与结论进行对比，在推导中利用了平方差公式、裂项相消法，从而实现了问题的解决.

二、“转化”思想在解题中的运用，简化过程提高思维方式

1.一般到特殊的思想转化

“任意”作为初中数学试题的关键词，具有一定的开放性，用特殊值法解这样的问题就非常高效和精确.

案例3：己知方程：（n+1）x4-（3n+3）x3-2nx2+18n=0，对于任意实数n，都会有一个相同的实数根，解这个方程.

分析：已知n为任意实数，就可以取较为简单的数进行代入计算.

解析：取n=0，则有x4-3x3=0，可得方程的解为x=3.

问题具有“任意”性，学生可以设立相对简单的数字进行分析，也可以让n=-1，对方程进行简化，简便快捷地得到答案.

2.抽象到直观的思想转化

初中试题中往往有一些抽象的问题，学生不能直观地看到问题之间的联系，如果将其变为图形试题，问题则会迎刃而解.

分析：学生对字母型的问题感到非常陌生，通过对问题的观察和分析，学生觉得与勾股定理有一定的相似，顺势就可以将问题转化为直角三角形问题.

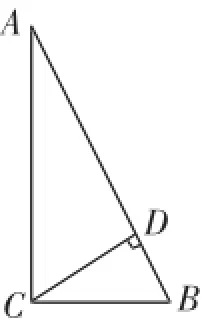
图1

解析：根据三角形的面积可得：S△ABC=

一道比较复杂的代数题，通过恰当的变形，转化为了有关直角三角形的图形问题，整个题显得生动直观了许多，问题的解决也就变得简单明了了.

三、“变式”训练在解题中的强化，灵活思考提高思维能力

“变式”训练主要根据题目的目标、内容、结构和特征等几个方面进行考虑，建立开放型的试题，主要包括一题多解、一题多变等几方面，促进学生从不同角度、不同层次进行探索学习，以提升学生的思维能力.

1.在一题多解中，培养学生思维的广阔性

一题多解帮助学生从多个方面进行分析，不仅夯实了基础知识，还拓宽了学生的解题思路，促进了学生知识运用的灵活性，充分做到了举一反三、融会贯通.

案例5：如图2所示，在△ABC中，D是AC上一点，AD∶DC=1∶2，BD的中点为E，且直线AE的延长线与BC的交点为F.试求BF∶FC的值.

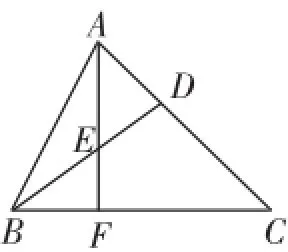
图2

分析：题中让求线段之间的比值，学生很容易就联想到了相似三角形和平行线中的比例关系，从而可以从不同的角度解决问题.

解法1：利用平行线分线段成比例的性质进行求解.过D点作AF的平行线，与BC相交于点N.

由BD的中点为E，得BF=FN.可以推得CM∶FM=CD∶ AD=2∶1，则CN=2FN=2BF，则BF∶FC=1∶3.

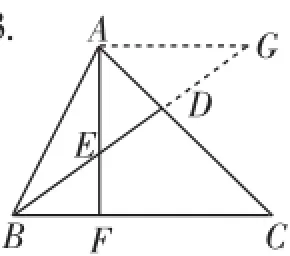
图3

解法2：利用相似三角形的性质进行求解.

如图3，过A点作平行于直线BC的直线，与BD的延长线交于点G.易得△AGD∽△CBD，则AG∶BC=GD∶BD=AD∶DC=1∶2，则GD=DE=BE.易得△AGE∽△FBE，则AG∶BF=GE∶BE=2∶1.由AG∶BC=1∶2，AG∶BF=2∶1，得BF∶CB=1∶4，则BF∶FC=1∶3.

解法3：利用三角形的面积比进行求解.

如图4，连接CE，过B点作AF的垂线于P，过C点作AF的垂线于AF的延长线上一点Q，从而得出△BFP∽△CFQ，则BF∶FC= BP∶CQ.由于AE既是△ABE的底又是△ACE的底，故S△ABE∶S△ACE=BP∶CQ= BF∶FC.因为△ABE与△ADE同底同高，故有S△ABE=S△ADE.则S△ADE∶S△ACE= BF∶FC.△ADE与△ACE同底，故有S△ADE∶S△ACE=AD∶AC=1∶3.因此BF∶FC=1∶3.

学生从不同的角度进行了分析，尝试改变自己的思路进行求解，在对比中了解了解题的繁简，长期的坚持有助于学生对最佳解法的掌握，很大程度上开阔了学生的思路，可促进学生解题能力的发展.

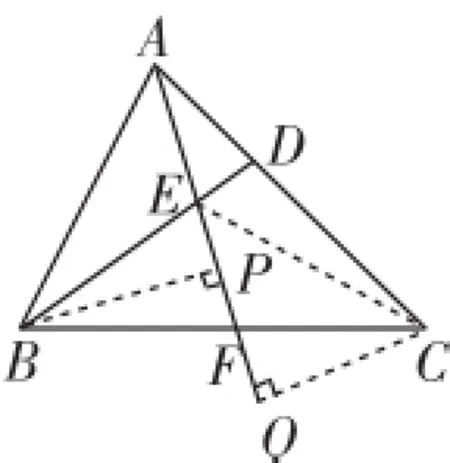
图4

2.在一题多变中，培养学生思维的敏捷性

一题多变是对题目结构进行变式，通过一个本质实现了问题的发散，调动学生对已有知识的回顾，将知识、技能、方法和思想进行灵活融合，极大地提高了学生的综合能力，提升了学生思维的敏捷性.

案例6：已知一次函数y=（3-k）x-2k+18，试求k的取值范围.

分析：本题重在考查一次函数的定义，那么教师就可以以此为例对问题进行变形，使学生深刻透彻地对一次函数进行学习.

变式1：一次函数y=（3-k）x-2k+18，该函数的图像必经过原点，试求k的值.

变式目的：考查图像、原点坐标和函数解析式之间的关系，令x=0，y=0，就可得到-2k+18=0，则k=9.

变式2：一次函数y=（3-k）x-2k+18，该函数与y轴有交点且在x轴的上方.试求k的值.

变式目的：考查一次函数与x轴、y轴的交点问题，与y轴有交点则x=0，且在x轴上方，说明-2k+18＞0，即k＜9.

变式3：一次函数y=（3-k）x-2k+18，y随x的增大而减小时，k为何值？

变式目的：考查一次函数的性质.3-k＜0，则k＞3.

变式4：一次函数y=（3-k）x-2k+18，其图像与直线y=-x相平行，试求k的值.

变式目的：考查直线的位置关系.

变式不是盲目的，而是要具有一定的计划性、针对性，使学生能够全面细致地了解知识的每一个方面.加强了学生思维的训练，切实做到了精讲、精练.

1.王林全.中学数学思想方法概论［M］.广州：暨南大学出版社，2003.

2.谭德胜.换个角度思考问题——也谈中学数学解题中的化归和转化思想［J］.理科爱好者（教育教学版），2012（3）.Z