法则引入与注重算理：运算教学的用力点

☉江苏省连云港市赣榆区欢墩中学 彭忠荣

法则引入与注重算理：运算教学的用力点

☉江苏省连云港市赣榆区欢墩中学 彭忠荣

我们注意到，《中学数学》（下）2015年以来刊载了多篇研究专家教师李庾南老师课例的文章，笔者十分赞赏这种研究取向，因为通过观摩、研究专家教师的课例设计、教学艺术，分析之后得到的就是研习者自身的专业成长，也即是从默会知识到“悠然神会，妙处与君说”的显性传递.于是，笔者找来李庾南老师前几年的教学录像——七年级“去括号”，反复观摩研习，现将该课的教学流程梳理出来，并跟进赏析，与同行分享.

一、“去括号”教学过程

（一）开课阶段：回顾学生已有的去括号经验

1.根据相反数的意义和表示方法去括号

（1）“相反数”的有关知识.

只有符号不同的两个数互为相反数，其中一个数叫做另一个数的相反数，正数的“+”可省略不写.在任意一个数前面添上“-”，新的数就表示原数的相反数.

（2）练、议.

根据相反数的意义化简下列各数：

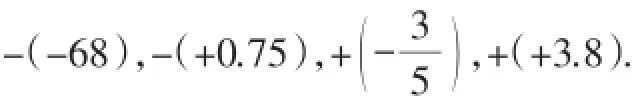
（3）概括练习中化简符号、去括号的方法.

括号前面是“+”时，由“正数的正号可省略不写”，将“+”和括号都去掉，括号内的数的符号不改变；

括号前面是“-”时，由相反数的意义，把括号和它前面的“-”去掉，括号里面的数改变符号.

2.根据有理数的乘法法则和乘法分配律去括号

（1）有理数乘法法则.

两数相乘，同号得正，异号得负，并把绝对值相乘，任何数同0相乘，都得0.

（2）乘法分配律.

一个数同两个数的和相乘，等于把这个数分别同这两个数相乘，再把积相加，即a（b+c）=ab+ac.

（3）练、议.

题1：计算5b+（-3b-2a）.

解：5b+（-3b-2a）……看作（+1）（-3b-2a）

＝5b-3b-2a……乘法分配律和乘法法则

＝2b-2a.

题2：13-（a-5）.

解：13-（a-5）……看作（-1）（a-5）

＝13-a+5……乘法分配律和乘法法则

＝18-a.

笔者说明：这里的运算并不是重点，多数学生都能顺利完成，重要的是教师在每一步后面都追问学生的变形依据，并注明算理.

教师解说：括号外的因数是正数，去括号后各项的符号与原括号内相应各项的符号相同；括号外面的因数是负数，去括号后各项的符号与原括号内相应各项的符号相反.

进一步反思讲评：根据加法的结合律和减法的运算性质去括号.

题1：5b+（-3b-2a）＝5b-3b-2a……加法结合律.

题2：13-（a-5）＝13-a+5……减法运算性质.

对于题2，也可以这样理解：一个数减去几个数的和，等于从这个数连续减去各个数.

（二）师生共同概括去括号法则

1.去括号法则

符号表示：a+（b-c）=a+b-c.

文字表示：括号前面是“+”，把括号和它前面的“+”去掉，括号里各项都不变号.

符号表示：a-（b-c）=a-b+c.

文字表示：括号前面是“-”，把括号和它前面的“-”去掉，括号里各项都改变符号.

2.练、议

合并下列各式的同类项：（教师要求学生注明第一步的依据）

（1）8a+2b+（5a-b）；（2）（5a-3b）-3（a2-2b）；

（3）3x-（4y-2x+1）；（4）-（x-y）+（-x-y）.

（三）由等式的对称性质“若a=b，则b=a”，概括添括号法则

1.去括号法则反过来为添括号法则

去括号法则添括号法则

2.添括号法则

添括号后，括号前面是“+”的，括到括号里的各项都不变号；

添括号后，括号前面是“-”的，括到括号里的各项都改变符号.

3.去、添括号符号法则的一致性

括号前面是“+”，去、添括号都不变号；

括号前面是“-”，去、添括号都要变号.

4.练、议，进一步理解添括号法则

例1在等号右边的括号内，填上适当的项：

（1）a+b+c-d=a+（）；……添带有“+”的括号

（2）a-b+c-d=a-（）；……添带有“-”的括号

（3）a-b-c-d=a-b+（）；……添带有“+”的括号

（4）a+b+c+d=a+b-（）；……添带有“-”的括号

（5）（a+b-c-d）（a-b+c-d）=［（a____）+（b______）］·［（a______）-（b_______）］.……添括号，学生们按题的特征自主选择填的项

例2（1）在多项式m4-2m2n2-2m2+2n2+n4中添括号.

要求：把四次项相结合，放在前面带有“+”的括号里；把二次项相结合，放在前面带有“-”的括号里.

解：m4-2m2n2-2m2+2n2+n4=（m4-2m2n2+n4）-（2m2-2n2）.

（2）把3x3-2x2-6x+4写成两个二项式的和.

教学记录：由于这是一个开放式问题，所以学生有不同的解答，如下所示.

解：3x3-2x2-6x+4=（3x3-2x2）-（6x-4）=（3x3-2x2）+（-6x+4）=（3x3-6x）+（-2x2+4）.

（四）去、添括号法则的应用练习

（1）计算（8xy-3x2）-5xy-2（3xy-2x2）.

（2）化简2a-3b+［4a-（3a-b）］.

（4）三角形的第一边是a+2b，第二边比第一边小（b-2），第三边比第二边小5，计算三角形的周长.

教学记录：这4道习题教师都要求不仅会做，还要能讲每一步的运算依据，即算理.其中第二题学生的不同解法如下所示.

解法1：2a-3b+［4a-（3a-b）］

＝2a-3b+4a-（3a-b）……先把（3a-b）看作一个整体，化去带有“+”的中括号

＝2a-3b+4a-3a+b……化去带有“-”的小括号

＝（2+4-3）a-（3-1）b……合并同类项时，添加括号

＝3a-2b.

解法2：2a-3b+［4a-（3a-b）］

＝2a-3b+（4a-3a+b）……先去小括号

＝2a-3b+（a+b）

＝2a-3b+a+b

＝3a-2b.

对于第四题，不少学生的解法中没有文字表达，全是字母运算，教师在订正时规范如下所示的解法步骤.

解：由题意知：—边为a+2b；

第二边为（a+2b）-（b-2）……添括号

＝a+2b-b+2……去括号

＝a+b+2；

第三边为（a+b+2）-5……添括号

＝a+b+2-5……去括号

＝a+b-3.

所以该三角形的周长为（a+2b）+（a+b+2）+（a+b-3）……添括号

＝a+2b+a+b+2+a+b-3……去括号

＝3a+4b-1.

（五）师生小结，布置作业

（1）在化简、计算等解决问题的过程中，有时需要添括号，有时需要去括号，必须掌握去、添括号法则.

（2）去、添括号法则中，括号与其前面的符号为一个整体，同时去、同时添，去、添括号的符号法则是一致的.

（3）去、添括号是两个互逆过程，可相互检验变形过程的正误.

二、课例赏析

以上梳理了李老师关于去括号教学的教学过程，其中有些来自课堂中的学生生成，有些是教师的点评或示范，并附有笔者的听课随感，以下再从整体上给出两点赏析.

1.运算法则教学要引导学生感受法则的合理性、和谐性、一致性

从开课阶段看似冗长的课堂引入来看，这节课是整式加减前的一个去括号法则，为什么不直接引入或介绍去括号法则，而要九曲十八弯地复习到上一章中有理数的诸多性质呢？这其实就是作为专家教师对数学知识前后一致、逻辑连贯的深刻理解，因为在学生有理数学习过程中，对于相反数、乘除法则等运算的学习，已经涉及去括号的思想或方法，这时教者通过复习这些旧知，目的是启发学生类比、归纳、概括出新知——“去括号”法则，而且在此过程中，一个新法则（或新约定），它的合理性、和谐性、一致性就被前面的引入环节铺垫得非常到位.这样的教学比之“一个法则，三项注意、几道例习题训练”（章建跃语）式教学要高明得多，与那种贴标签式的强调去括号具有合理、和谐、一致的点评相比，也有着更为高超的“无痕”教学艺术.此外，大家是否注意到，目前教材上在该节教学时并没有添括号法则，然而上面的教学中，李老师却基于“反过来”的思考，引导学生概括小结了添括号法则，教学过程非常自然，学生接受得也很好，这并不是增加学生的课业负担，而是完善了知识体系，让学生加深了知识之间的和谐共生、逻辑一致的认识，专家教师对教学内容的深刻理解值得深思.

2.运算教学应该在重视算理的基础上追求运算速度

中科院李文林研究员曾指出，数学就是两个字：算和证.就我们所见，当前教学中对运算的要求是高的，学生进行繁杂运算的能力是强的，一方面有应试的压力，另一方面与我们过分拒绝使用计算器也不无关系.然而，对于算理的重视却不够到位.表现在运算教学中，我们过分重视了大量的运算演练，让学生通过过度的机械训练来达到“熟能生巧”的运算教学目标.而我们从李老师的教学中能发现，她的这节课并没有安排大量的、形形色色的运算训练，而是注意在有限的几个练习中开展算理的追问、标注，并倡导学生在独立运算之后的小组议论、全班交流，注意每一步运算的依据和算理的训练.笔者以为，这即是一种高水平的数学教学.运算教学的新课期间，如果不能充分重视算理，就匆匆追求所谓的运算速度是本末倒置.

1.朱映红.情境创设再认识：值得重视的“超经验”——李庚南老师“二元一次方程组”起始课赏析［J］.中学数学（下），2015（4）.

2.吴燕飞.找准生长点，思辨特殊与一般——李庚南老师“直角三角形全等”课例赏析［J］.中学数学（下），2015（4）.

3.李庾南.自学·议论·引导教学论［M］.北京：人民教育出版社，2013.

4.钟启泉.新旧教学的分水岭［J］.基础教育课程（上），2014（2）.

5.章建跃.构建逻辑连贯的学习过程使学生学会思考［J］.数学通报，2013（6）.

6.李庾南，陈育彬.中学数学新课程教学设计30例——学力是这样发展的［M］.北京：人民教育出版社，2007.

7.刘东升.悠然神会，妙处与君说——李庾南老师“平方根”课例赏析［J］.中国数学教育，2014（5）.Z