适时“留白”，让学生展示精彩

☉山东省沂源县实验中学 崔春近

适时“留白”，让学生展示精彩

☉山东省沂源县实验中学 崔春近

想到了国画和书法应该是疏密有致，疏处可以走马，密处不使透风，在课堂教学中适时“留白”，让学生展示精彩，同样会收到不一样的效果.在课堂中，教师让学生充分展示自己的才华，通过学生的自主探究、小组交流，学生学会了如何在已知与未知之间架起一座“桥梁”，实现了学习方式由被动接收式向主动探究式的根本转变.教师以问题为背景依托，充分拓展学生思维的空间，让学生在探究中学习，在不知不觉中锻炼提升了自己的思维.下面，笔者结合自身的教学和教学活动中的所见、所感、所想，谈自己的粗浅认识.

一、引而不发，在方法拓展时“留白”

题目1：（2013·呼和浩特·16）在平面直角坐标系中，已知点A（4，0）、B（-6，0），点C是y轴上的一个动点，当∠BCA=45°时，点C的坐标为__________.

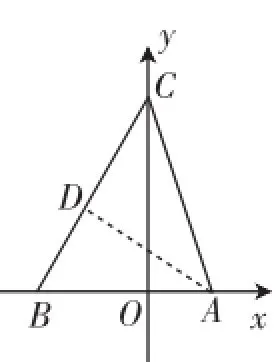
图1

分析：本题在十字坐标系中给出了A、B两点的坐标，让我们在y轴上寻找一点，使得∠BCA=45°，解题的关键在于怎样利用∠BCA=45°这一条件，如何将∠BCA=45°这一条件进行转化.本想根据笔者自己的教学预设给学生讲解，在课堂中自己把问题放手给学生，听一听学生的分析思路，却收到了意外的惊喜.生1：我是利用面积相等法来求解的.具体过程如下.当C点在y轴的正半轴时，如图1，作AD⊥BC于点D，设OC=h，则为∠BCA= 45°，所以据BC·AD=BA·OC得到解得h2=144或h2=4（不符合题意，舍去），所以h=12，所以C点的坐标是（0，12）.

同理，当C点在y轴的负半轴时，可以得到C点的坐标是（0，-12）.

（主要是考虑到∠BCA=45°，然后过点A作AD⊥BC于点D，这样就构造出了等腰直角三角形ACD，然后利用面积相等列出了等式，这一种方法比较好理解，但是计算上比较麻烦，方程中出现了四次方，对于学生们的计算能力是一个挑战）

生2：我是构造等腰直角三角形，利用面积分割来求解此题.如图2，过B作BD⊥BC与CA的延长线相交于一点D，然后作DD′⊥x轴于D′.因为∠BCA=45°，所以三角形BCD是等腰直角三角形，BD=BC.易证Rt△BDD′≌Rt△CBO，所以DD′=6.

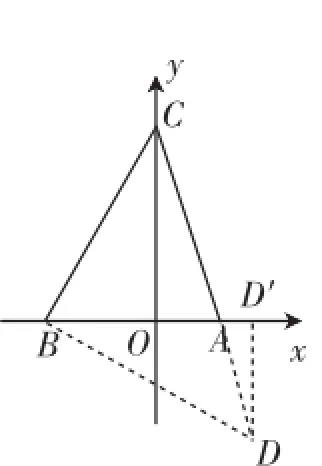
图2

（还是考虑到∠BCA=45°，构造等腰直角三角形BCD，同时还构造出了一对全等三角形，然后利用面积分割列出了等式，这一种方法省去了学生1计算4次方的麻烦，但是构造上有一定的技巧性）

生3：我也是构造等腰直角三角形，利用相似来求解此题.我的辅助线的作法与学生2的相同，过B作BD⊥BC与CA的延长线相交于一点D，然后作DD′⊥x轴于D′.因为∠BCA=45°，所以三角形BCD是等腰直角三角形，BD= BC.很容易证Rt△BDD′≌Rt△CBO，所以DD′=6.设OC= h，则AD′=h-10.根据Rt△AOC∽Rt△AD′D，得解得h=12或h=-2（舍去），所以C点的坐标是（0，12）.

（还是考虑到∠BCA=45°，构造等腰直角三角形BCD，同时还构造出了一对相似三角形，然后利用相似三角形的对应边成比例列出了等式）

生4：我是利用轴对称求解的.如图3，作三角形BCA关于AC的对称三角形ACD，连接BD与AC相交于点E，与y轴相交于点F，过D作DD′⊥y轴于点D′.很容易证Rt△BAE≌Rt△CFE，所以CF=10.又因为Rt△CDD′≌Rt△BCO，所以CD′=6，D′F=4，DD′=OC.设OC=h，由△DD′F∽△BOF，得h=12或h=-2（舍去），所以C点的坐标是（0，12）.

（利用轴对称构造了三个等腰直角△BCD、△BCE、△CDE，然后通过两次全等、一次相似来求解，在求解过程中体现了构造的思想，并充分利用全等、相似的相关知识求出结果）

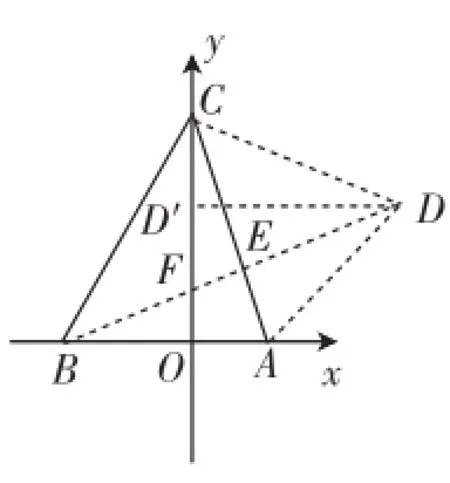
图3

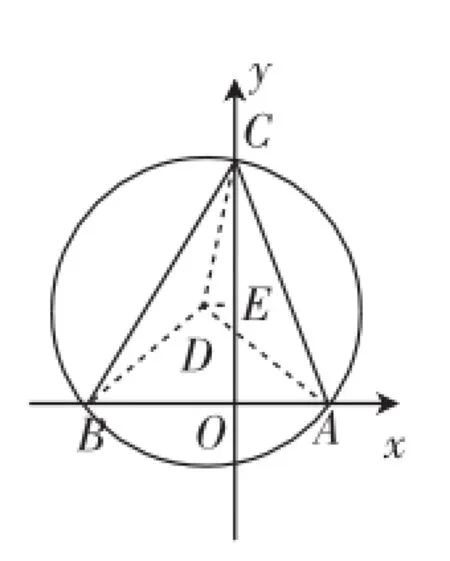
图4

生5：利用辅助圆来求解.如图4，作△ABC的外接圆，圆心为D，因为∠BCA=45°，所以∠BDA=90°.易求得AD= BD=作DE⊥y轴，垂足为E，因为DE=1，CD=所以CE=7.又因为OE=5，所以C点的坐标是（0，12）.

（利用辅助圆中圆周角和圆心角的关系，将∠BCA= 45°这一条件转化，轻松地将问题转化）

生6：我是利用相似、全等来求解的.具体过程如下.

如图5，作AD⊥BC于点D，与y轴相交于点E.因为CD=AD，所以Rt△DBA≌Rt△DEC，所以CE=10.设OE=x，因为Rt△AOE∽Rt△COB，x2+10x-24= 0，解得x=2或x=-12（不符合题意，舍去），所以x=2，所以C点的坐标是（0，12）.

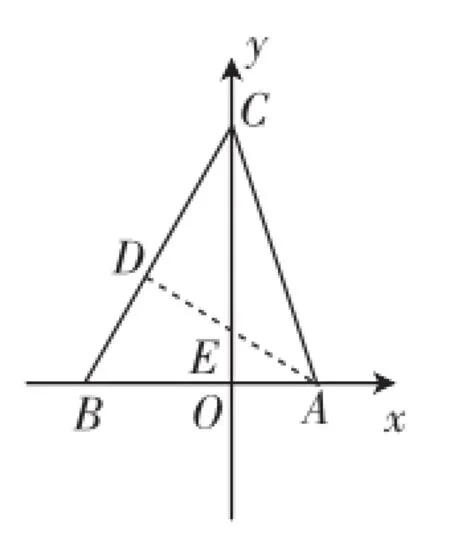
图5

图6

生7：通过翻阅高中课本，我是利用直线到直线的角来求解的.设C点的坐标为（0，a），理得a2-10a-24=0.解得a=12或a=-2（舍去），所以C点的坐标是（0，12）.

（直接根据直线BC到直线AC的角是45°，利用夹角公示就可以直接求出结果.但是公式的内容超出了初中教材，需要自己课下提前学习才行）

生8：利用轴对称构造正方形，运用勾股定理求解.如图7，作三角形BCO关于BC的对称三角形DCB，同理，作三角形AOC关于AC的对称三角形ACE.易证∠DCE=90°.又因为∠D=∠E=90°，所以延长DE与EA相交于点F，则四边形CDFE是正方形.设OC=h，则BF=h-6，AF=h-4.在Rt△ABF中，由勾股定理可得（h-6）2+（h-4）2=100，解得h=12或h=-2（舍去），所以C点的坐标是（0，12）.

（利用轴对称构造出了正方形，当然，这里面运用了矩形、正方形的判定，然后运用勾股定理求出答案，方法十分巧妙）

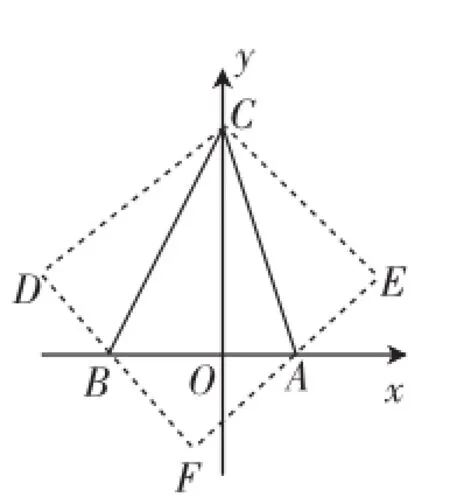
图7

二、观而不理，在思维冲突前“留白”

题目2：如图8，△ABC中，CD⊥AB于点D，下列条件中，一定能确定△ABC是直角三角形的是：①∠A+∠B=90°，②AC2+BC2= AB2，③AB·CD=AC·BC，….

学生对于①、②没有什么疑问，但对于③却展开了激烈的争论.

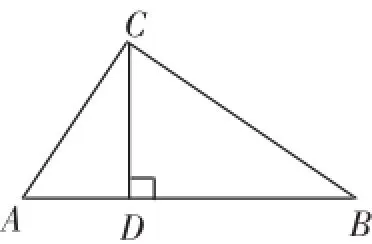
图8

生1：此条件不能确定△ABC是直角三角形，由AB· CD=AC·BC，得△ABC与△BCD的公共角是∠B，这是两边成比例，其中一边的对角相等，不能够证明△ABC∽△BCD，所以不能确定△ABC是直角三角形.

（大部分同学认为学生1的分析有道理，教师也点头认可，学生2的分析却让课堂再现“波澜”）

生2：此条件可以判定∠ACB=90°.

（同学们都投入了异样的目光）

（师生都为生2的精彩讲解喝彩，不约而同地为学生2的表现鼓掌）

生3：学生2的分析不正确，我们可以设AB=6，CD=2，AC=3，BC=4，此时，AC2+BC2≠AB2，那么，△ABC不是直角三角形.

（生3通过这一举例，让生2的分析陷入了尴尬，高潮过后的“平静”又起“风波”.这时，老师只有在一旁静静地等待，课堂是学生的课堂，学生的头脑也并非容器，而是等待被点燃的火种！教师要给机会，留出时间，给学生更大的空间，特别是思维的空间，使课堂正真成为学生学习的舞台.要让学生战胜知识的抽象，享受到成功的快乐）

生4：学生3的举例不可以，若AC=3，CD=2，则AD=，若BC=4，CD=2，则BD=所以AB=所以对于AB、CD、AC、BC不能够随便赋值.

（问题在不断地讨论中落下帷幕，肖川语：“教育的过程就是一个不完美的人引领着另一个不完美的人追求完美的过程，我们永远走在‘趋于完美’的路上，而达到‘知行合一’需要一个过程.”所以教学的过程是不断探究的过程，是突破思维定势、大胆创新的过程.探索的过程充满艰辛与苦恼，发现问题的根源所在可谓是历尽“磨难”，方成正果.整个问题的探究，学生自由发言，师生共同营造了一个“平等、民主、亲密、宽松”的教学氛围，学生积极动脑，大胆发言，当问题出现时，教师期待的目光激发了学生学习的热情，探究的愿望油然而生.学生身临其境的探究活动，使学生更清晰地明白了前因后果）

三、导而不为，在“困难”面前“留白”

题目3：在如图9所示的直角坐标系中，点A的坐标是（3，4），点A绕着原点O逆时针旋转90°得到点B，点B再绕着原点O逆时针旋转45°得到点C，求点C的坐标.

分析：题目设置在直角坐标系中，点A绕着原点O逆时针旋转两次，然后求两次旋转后点C的坐标，题干“精炼”，但细细分析又感觉无从下手，不知如何去利用已知条件，怎样找到解决问题的“突破口”呢？

备课组内教师也对此题进行了探究讨论.

教师1：我们可以设A点的坐标为（5cosθ，5sinθ），则C点的坐标为（5cos（θ+135°），5sin（θ+135°））.因为cos（θ+

（尽管这一思路易于理解，计算量也不是很大，但教师们都对这一求解思路持否定意见，因为此法运用了高中三角函数的知识，已超出了学生的接受水平.对于初中生来说很难理解，必须另辟蹊径）

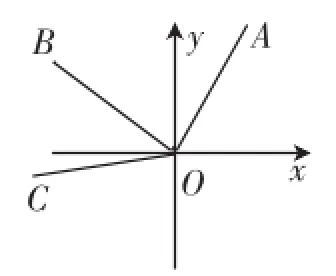
图9

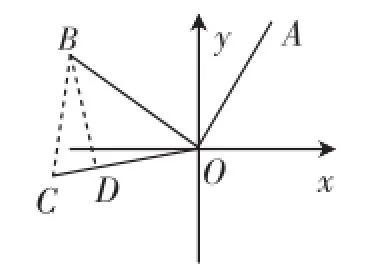
图10

教师2：如图10，连接BC，过B点作BD⊥OC.设C点的坐标为（x，y），根据题意x2+y2=25①.又因为点B的坐标为

（这一思路很清晰，也易于理解，主要运用点C到原点的距离是5，还有B、C两点间的距离就可以求出C点的坐标.但需要求解一个二元二次方程组，对于学生的计算能力是一个挑战.教师们一致决定，把这一题目作为一个探究性问题与学生一块分析探究，共同找到最佳的解决方案.数学教师的教学水平也只有在解题探究的过程中才能体现，“常在河边走，哪能不湿鞋”，关键是如何去面对问题，每个学生都有无限的创造潜能，关键是老师的启发、引导和鼓励）

课堂上教师引导，师生共同探究，将问题一步步转化，思路一步步清晰，方法也越来越简单.

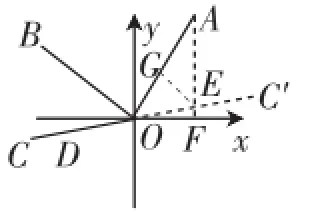
图11

思路1：如图11，反向延长CO到C′，使得OC′=OC，过点A作AF⊥x轴于F，交OC′于点E，过E作EG⊥OA，设GE=x.因为∠AOC′=45°，所以OG=x.在Rt△AGE坐标C点的坐标为

思路2：如图12，过A点作AD⊥OA，与CO的延长线交于D，作AE⊥x轴于点E，过点D作DF⊥AE于点F.因为∠OAD=∠AFD=90°，所以∠OAE=∠ADF.又因为AD= OA，所以△AOE≌△DAF，所以AF=3，FD=4，所以D点的坐标为（7，1）.又因为线段OD与线段OC关于原点位似，

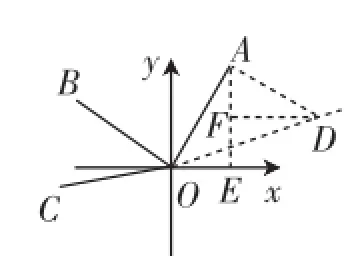
图12

图13

思路3：如图13，过A点作AD⊥OA，与CO的延长线交于D，连接AB.因为∠BOA=∠OAD=90°，∠AOD=∠OAB= 45°，所以BO∥AD，OD∥AB，所以四边形ODAB是平行四边形.因为OA的中点的坐标为（-4，3），所以D点的坐标为（7，1）.又因为线段OD与线段OC关于原

题海无边，教师想在有限的时间内把题海中的无数条鱼都“捕杀殆尽”，显然是不可能的，唯有授人以渔，在问题探究中，根据实际为学生搭建探究和展示的舞台，让学生在探究中不断改进，在不断改进中提升自己的能力，才能把学生从题海中拉出，才能让学生以不变应万变，从容于数学学习之中.Z