关联变式打磨新题——由一道扇形翻滚中考模拟试题谈起

☉江苏省无锡市硕放中学 邹黎明

☉江苏省无锡市新城中学 浦叙德

·江苏省无锡市浦叙德名师工作室·

关联变式打磨新题
——由一道扇形翻滚中考模拟试题谈起

☉江苏省无锡市硕放中学 邹黎明

☉江苏省无锡市新城中学 浦叙德

最近，由于要命制2015年中考数学模拟试题，我们对中考数学中扇形翻滚类试题进行思考，由于图形的运动既有旋转又有滚动，因此，对于学生来说，确实有一点困难.我们对于这种试题进行了解析，揭示其本质，并发掘出一些变式，颇有新意，写成一文供参考.

一、原题

题目（2009年盐城市二模）如图1，将半径为1、圆心角为60°的扇形纸片AOB，在直线l上向右做无滑动的滚动至扇形A′O′B′处，则顶点O经过的路线总长为__________.

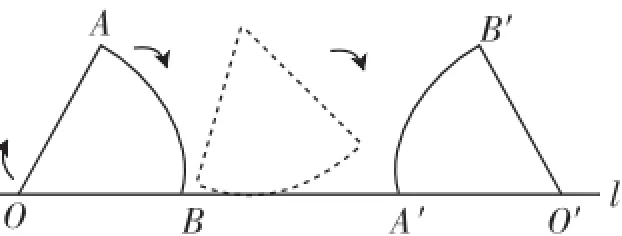
图1

分析：这个题目的关键是要把整个扇形翻滚变化描述清楚，还要把变化的临界情况弄明白.

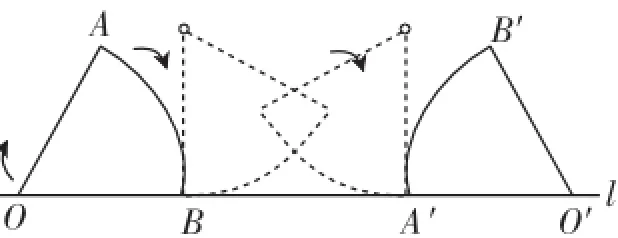
图2

如图2，点O所走路线分三步：第一步，从开始至OB半径与直线l垂直，OB绕点B旋转了90°，半径为1；第二步，从OB与直线l垂直滚动至OA与直线l垂直，O点的路径是一段线段，长周长；第三步，从半径OA与直线l垂直到终止，OA绕点A旋转了90°，半径为1.故 O点走的路线总

二、变式

变式1：（2015年无锡市新区一模第17题，命题人邹黎明）如图3，扇形OMN与正三角形ABC，半径OM与AB重合，扇形中弧MN的长为AB的长，已知AB=10，扇形沿着正三角形翻滚到首次与起始位置相同，则点O经过的路径长为__________.

分析：题目中“扇形沿着正三角形翻滚到首次与起始位置相同”，是指O与A、B与M重合，这个题目顺向、逆向答案一样，一周就可以.

如图4，第一步，扇形绕点B旋转360°-90°-60°=210°，这个时候OM⊥BC于点B，O的路径长是半径为10的一段弧长；第二步，圆弧在BC上滚动，点O经过BC长，即为10，这个时候ON⊥BC于点C；第三步，绕点C旋转210°，半径为10的一段弧长，这个时候NO与CA重合；第四步，在点O与点A重合的前提下，绕点O旋转到OM与AB重合，故点

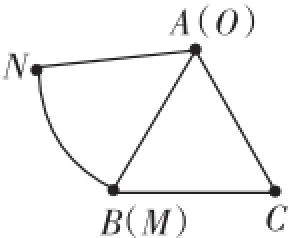
图3

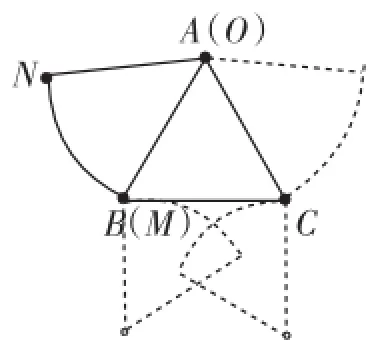
图4

过程追踪：可以看出对于点O经过的路径，可以分解为：旋转有以O为圆心的路径为0，以M或N为圆心的路径长相等，为了区别分别记为lM、lN，滚动路径长为扇形半径长，记为R.

顺向：0、lN、R、lM，这时点B与点M重合，这样，首次与起始位置相同.逆向：lM、R、lN、0，这时点O与点A重合，这样，首次与起始位置相同.显然，总路径长相等.

变式2：如图5，扇形OMN与正五边形ABCDE，半径ON与AB重合，扇形弧MN的长为AB的长，已知AB=10，扇形沿着正五边形逆时针翻滚到一条半径首次与AB重合，点O经过的路径长为__________.

分析：题目中“扇形沿着正五边形逆时针翻滚到一条半径首次与AB重合”，与变式1要求不同，没有要求点O与点A、点B与点N重合.

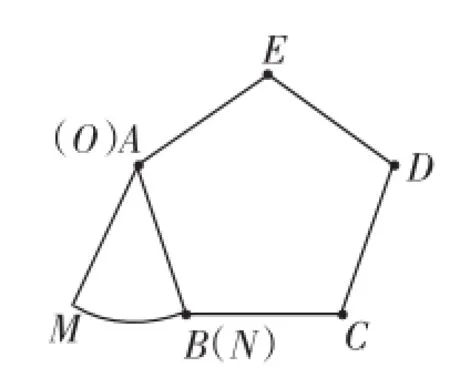
图5

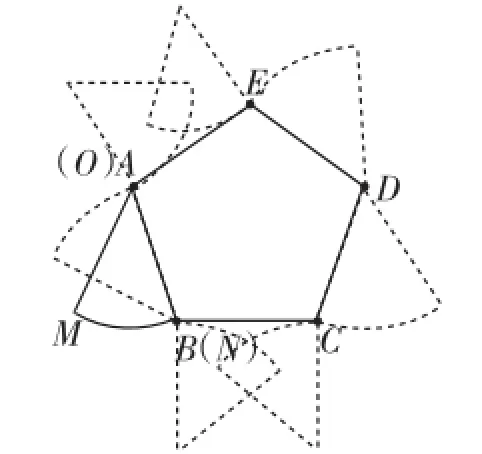
图6

过程追踪：如图6，逆向：lN、R、lM、0、lN、R、lM，这时点M与点A、点B与点O分别重合，没有回到起始位置.lN、lM相应的旋转角度都是360°-90°-108°=162°.所以长为4×

思考1：题目中“扇形沿着正五边形逆时针翻滚到一条半径首次与AB重合”，改为“扇形沿着正五边形顺时针翻滚到首次与AB重合”，则点O经过的路径长为_________.

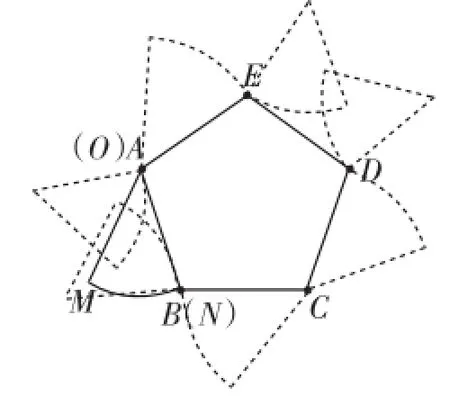
图7

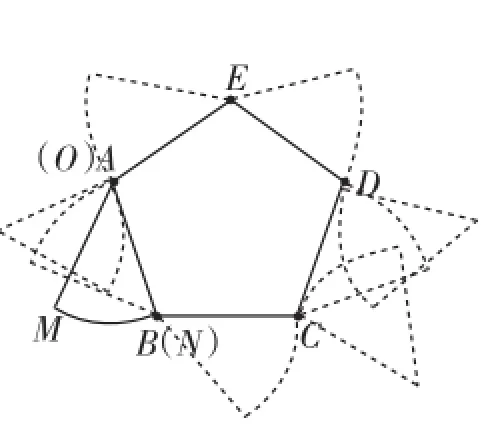
图8

分析：顺时针翻滚从图7看出第一周没有翻滚到一条半径首次与AB重合，如图8第二周才是，虽然都是这个位置，但还不是“首次与起始位置相同”.

过程追踪：顺时针翻滚：0、lM、R、lN、0、lM、R、lN、0、lM、R、lN、0，这时点M与点A、点O与点B重合.从图7看出第一周没有翻滚到一条半径首次与AB重合，这时第一周3×如图8第二周的路径长为27π+ 10，合起来为54π+30.

思考2：题目中“扇形沿着正五边形逆时针翻滚到一条半径首次与AB重合”，改为“扇形沿着正五边形翻滚到首次起始位置重合”，则点O经过的路径长为__________.

分析：考虑顺时针，我们发现要三周.

过程追踪：顺时针翻滚：0、lM、R、lN、0、lM、R、lN、0、lM、R、lN、0，lM、R、lN、0、lM、R、lN，加上如图9所示的第三周路径长，可以看出每次旋转角度都是90°次滚动都是10.

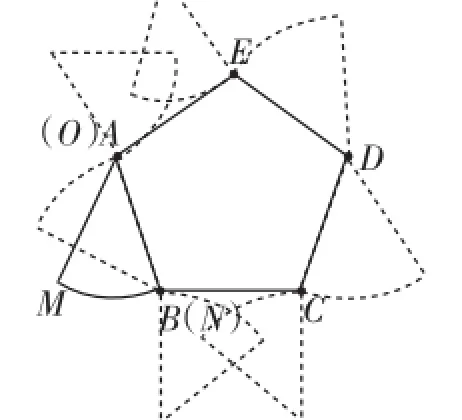
图9

我们可以得到逆时针结果一样.

三、推广和联想

一般地，如果题目中改为正n边形，其他条件如变式1扇形沿着正n边形翻滚到首次起始位置重合，求点O经过的路径长.

（2）n是3的倍数，n=3m，只要1圈就可以了，有2m个

问题还可以变成在矩形、菱形、梯形外面翻滚.

变式3：如图10，在矩形ABCD中，AB=a，AD=2AB，扇形OMN，OM与AB重合，弧MN的长等于AB的长，扇形沿着矩形翻滚到首次与起始位置相同，则点O经过的路径长为__________..

图10

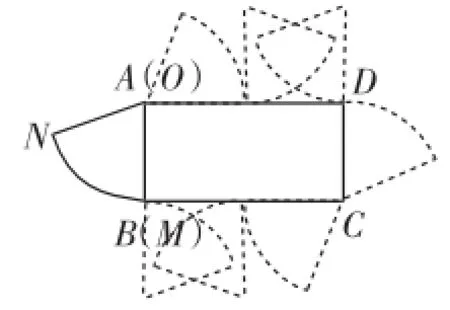
图11

分析：如图11，这个变式中扇形沿着矩形翻滚一周就可以首次与起始位置相同，而且顺向、逆向答案一样，分别旋转角度为90°、180°、90°、180°；滚动两次，点O经过

因此，只要理清这些题目运动节点，画出相关“轨迹”，寻找路径长的循环节，就找到了问题的解决方法.变换有关图形的数据，就可以编拟各种难度的试题.因为这种题目符合初中数学实验创新的内容，但教师平时教学中很少注意这部分内容，特别是《苏科版数学实验手册》利用率不高，因此，这种题目学生解答的准确率比较低，希望教师在教学这类问题的同时，能够引起对“数学实验”教学的重视，在课堂或课外活动中积极实施.H