基于卷对卷矩形靶的溅射膜厚均匀性控制*
黄云翔 温万昱 孙佳伟 槐创锋 曾海峰 钟褔回
(1.华南理工大学 表面功能结构先进制造广东普通高校重点实验室, 广东 广州 510640;2.阳江市汉能工业有限公司 铜铟镓硒(CIGS)薄膜太阳能电池研制及推广中心, 广东 阳江 529533)
基于卷对卷矩形靶的溅射膜厚均匀性控制*
黄云翔1温万昱1孙佳伟1槐创锋1曾海峰2钟褔回2
(1.华南理工大学 表面功能结构先进制造广东普通高校重点实验室, 广东 广州 510640;2.阳江市汉能工业有限公司 铜铟镓硒(CIGS)薄膜太阳能电池研制及推广中心, 广东 阳江 529533)
提出一种基于卷对卷矩形靶的溅射理论模型,借助Matlab模拟仿真软件,对卷绕柔性衬底(宽度为100 mm,弯曲半径为100 mm,弯曲角为80°)的膜厚均匀性进行分析.首先,在主辊静态条件下,改变靶材几何尺寸和靶基距,研究此时膜厚均匀性误差的分布情况,发现:膜厚均匀性误差随着靶材几何尺寸的变大而整体减小;随着靶基距的增大,均匀性误差的中部先增大后减小,而两边一直减小.其次,在主辊动态条件下,固定靶材几何尺寸,仅改变靶基距,研究此时膜厚均匀性误差的分布规律,发现:随着靶基距的增大,膜厚均匀性误差先增大后减小.仿真实验结果还表明,动态膜厚均匀性误差位于静态膜厚均匀性误差分布曲线Max-Min的中部极值点与该分布曲线上参考点均值之间.通过对文中模型的仿真,可以较快地预测基于卷对卷矩形靶的动态膜厚均匀性误差范围,大大减少膜厚均匀性的实验调试次数.
矩形靶;卷对卷;真空磁控溅射;膜厚均匀性;仿真
真空磁控溅射镀膜法具有生产成本低、重复性好和成膜表面质量高的优点,广泛应用于薄膜制备.膜厚均匀性是衡量薄膜质量的一项重要指标,有效地控制膜厚均匀性已成为溅射镀膜的一个技术难点.通常,膜厚均匀性会受到磁控溅射源、靶材几何尺寸、靶基距以及靶和基片之间相对运动的影响.
目前,通过数学建模和计算机仿真实验开展平面基片膜厚均匀性的研究工作已比较普遍.Du等[1]根据cosnθ法则,采用数值分析方法,推导出了预测非对称溅射膜厚分布的简单、有效的计算公式,避免了过于繁琐的计算过程.Swann等[2]建立了圆形靶膜厚分布的计算机数学模型,通过改变靶基距和偏离对称轴距,研究膜厚均匀性的变化规律,并通过实验验证了模型的有效性.Zhang等[3]建立了基于矩形靶的膜厚分布模型,并运用Matlab软件模拟仿真,详细地分析了膜厚均匀性在不同靶材几何尺寸和靶基距条件下的变化规律.Jiang等[4]建立了基于旋转平面基片和步进圆形平面靶位相结合的膜厚分布理论模型,模拟了大面积基片的膜厚均匀性在不同的靶基距和基片与靶位相对速度比率下的沉积规律.Fu等[5]建立了基于旋转平面基片的膜厚分布理论模型,模拟了膜厚均匀性在不同的自转速度、公转速度和靶基距下的变化规律.Fan等[6]建立了基于对称磁体磁控溅射(SMMS)设备的膜厚分布理论模型,推导出了任意靶基距下的膜厚分布规律,该理论模型可应用于其他维度的SMMS系统.由此可见,计算机模拟仿真是研究溅射膜厚均匀性的有效手段和关键技术.
相对于不连续的平面基片溅射镀膜方式,连续化的卷对卷溅射镀膜具有降低生产成本和提高生产效率的优势,目前已广泛应用于多种薄膜材料的制备[7- 9].在不连续的大面积批量化溅射镀膜生产中,平面基片膜厚均匀性的控制可以通过使用大面积固定矩形靶与往返移动载片工作台相结合的溅射系统来实现,也可以通过利用小面积固定圆形靶(单靶或多靶)与旋转载片工作台相结合的溅射系统来实现.然而,目前大多数的关于连续化、批量化的卷绕溅射镀膜系统的研究仅针对柔性基片上生长薄膜的沉积参数,如溅射功率、溅射气压、不同气体比例和衬底温度,对于卷对卷镀膜系统的薄膜均匀性控制参数(如靶材几何尺寸、靶基距和旋转速度)却很少涉及.卷绕溅射系统的膜厚分布理论数学模型也未见报道.
有鉴于此,为了完善卷对卷的镀膜技术,文中在原有平面基片矩形靶溅射的理论模型基础上,建立一套卷绕基片矩形靶溅射的理论模型.运用Matlab软件对该模型进行模拟仿真,研究靶材几何尺寸和靶基距对卷绕基片溅射膜厚均匀性的影响,最后获得卷绕矩形靶溅射膜厚均匀性的控制方法.
1 卷绕溅射模型的建立

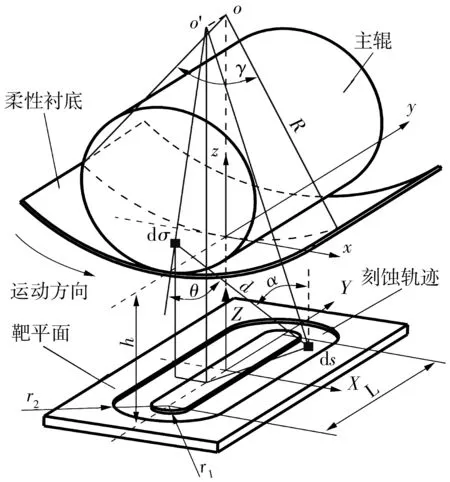
图1 卷对卷矩形靶的溅射几何参数示意图
Fig.1 Schematic diagram of geometric parameters of roll-to-roll rectangular target
根据图1所示几何关系可得
(1)
(2)
d2=(X-x)2+(Y-y)2+(h+z)2
(3)
磁控溅射一般工作在0.1~0.5Pa低气压下,以减小离子之间的碰撞概率,提高沉积效率.在这种条件下,有4个假设[10]可应用于平面矩形靶的磁控溅射,具体如下:(1)由于侵蚀区(刻蚀痕迹)附近分布了很强的磁场线,所有来自靶材侵蚀区的溅射粒子都均匀溅射且侵蚀速率恒定;(2)电场线总是垂直于导体表面,该路径上离子沿着电场线加速轰击靶材的入射角假定为0°;(3)假定沉积后沉积原子不扩散,溅射粒子的角度分布满足余弦分布;(4)溅射粒子直接从靶面飞向基片,其沉积速率与距离d成反比,在这种情况下气体压力约为几帕斯卡.
根据平面基片溅射理论[11- 12],膜厚可以通过式(4)计算,而式(4)则由式(5)-(7)化简得到:
(4)
(5)
式中,T为整个侵蚀区的沉积厚度,ρ为沉积膜密度,m′为沉积膜的质量,m为侵蚀区面微元的单位溅射质量,β为立体角.β、m′和T可分别由以下公式求得:
(6)
dm′=ρdTdσ
(7)
(8)
式中,DXY为图2所示的侵蚀区总面积.
通常,为了确保膜厚均匀性,会降低锐角效应[13],限定矩形靶的几何参数关系,具体如下:L/(2r2)≥3,r1≈r2/3.这里,假定L/(2r2)=3,r1=r2/3,如图2所示.
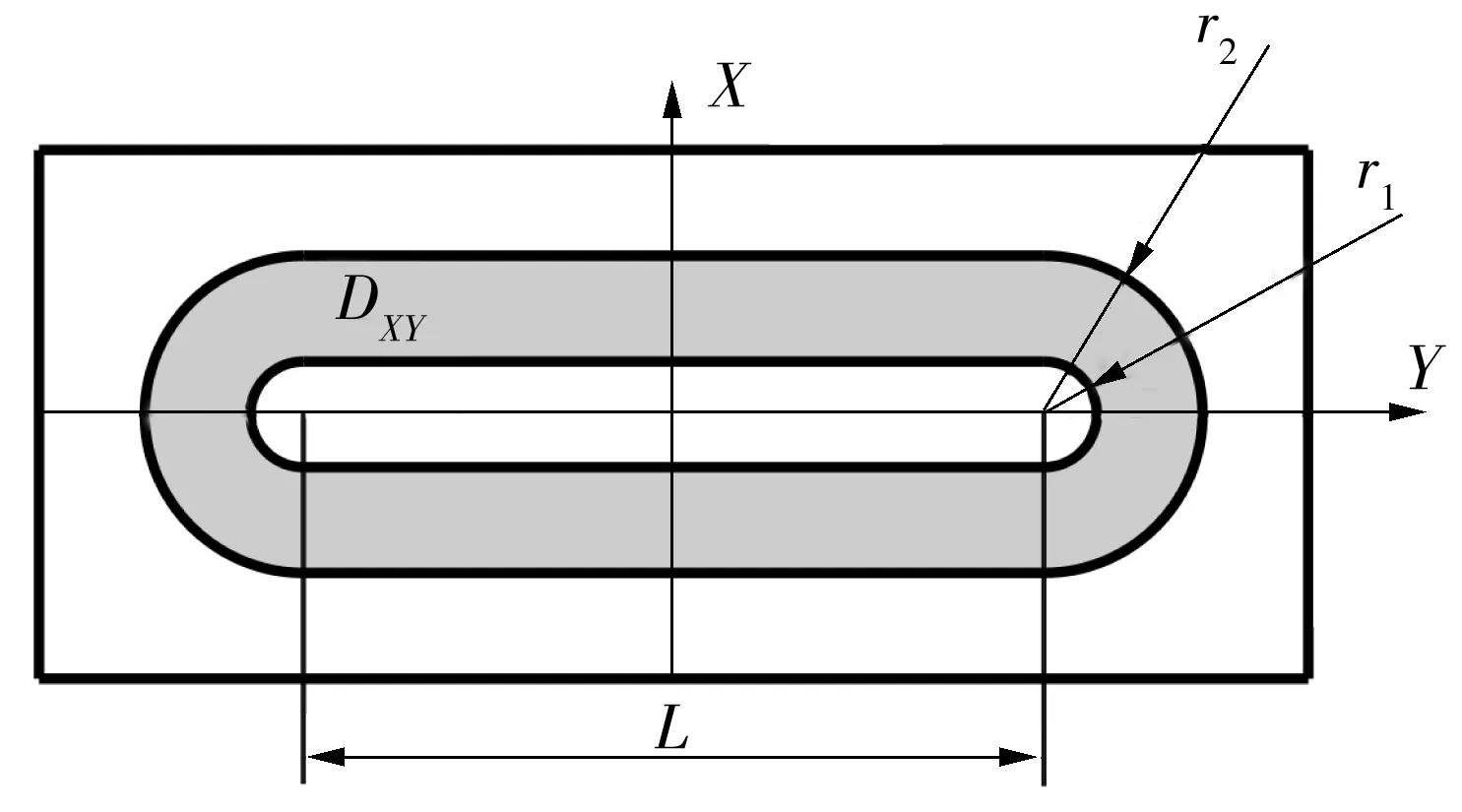
图2 矩形靶的侵蚀区示意图
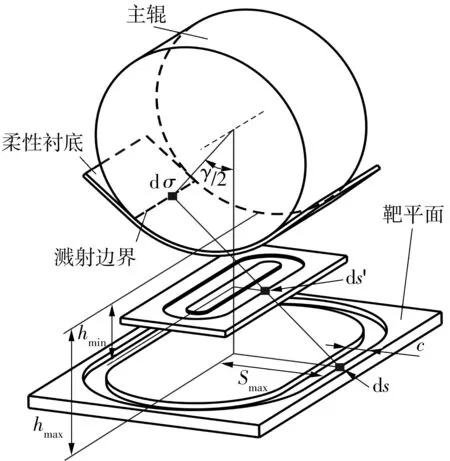
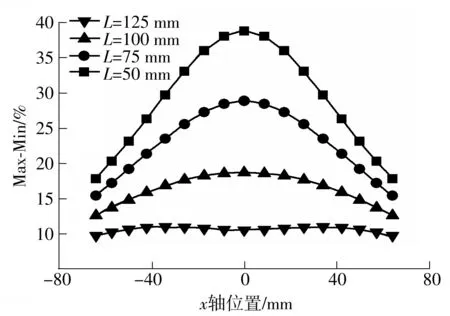
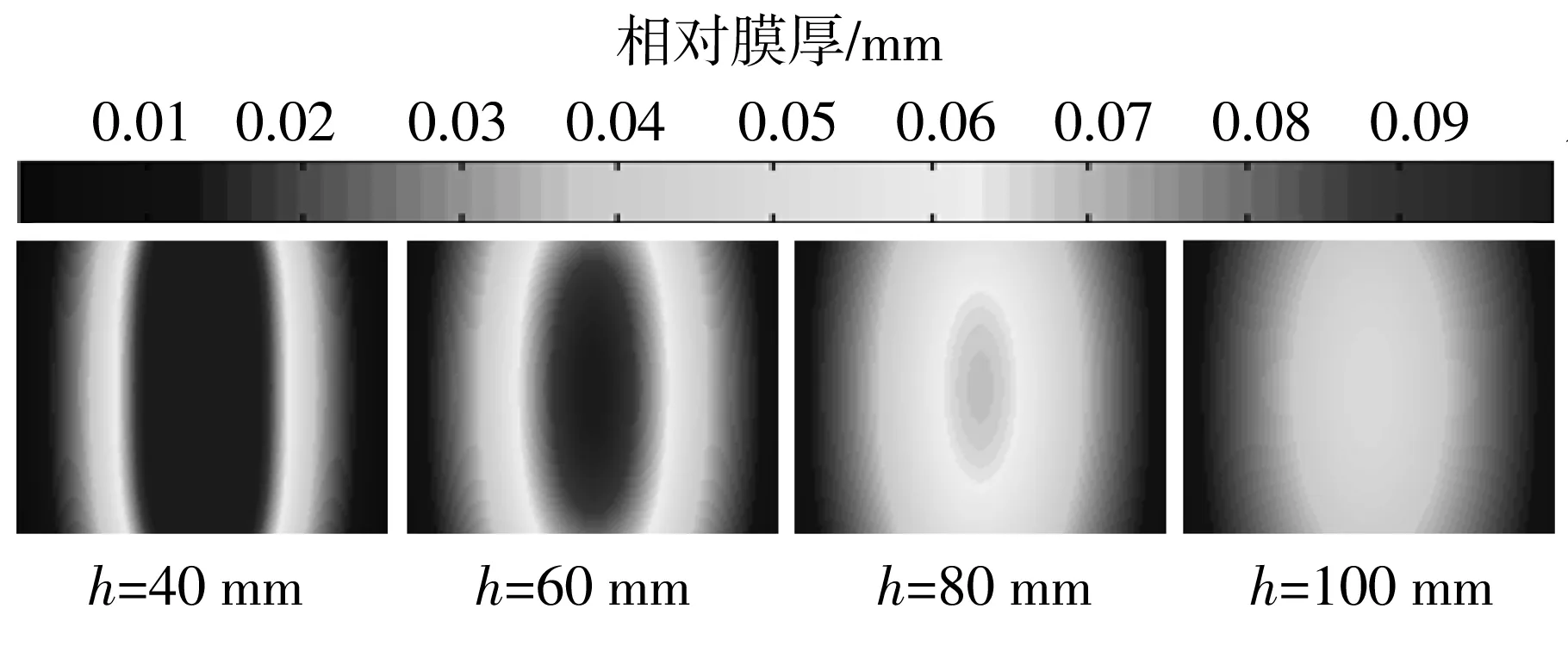
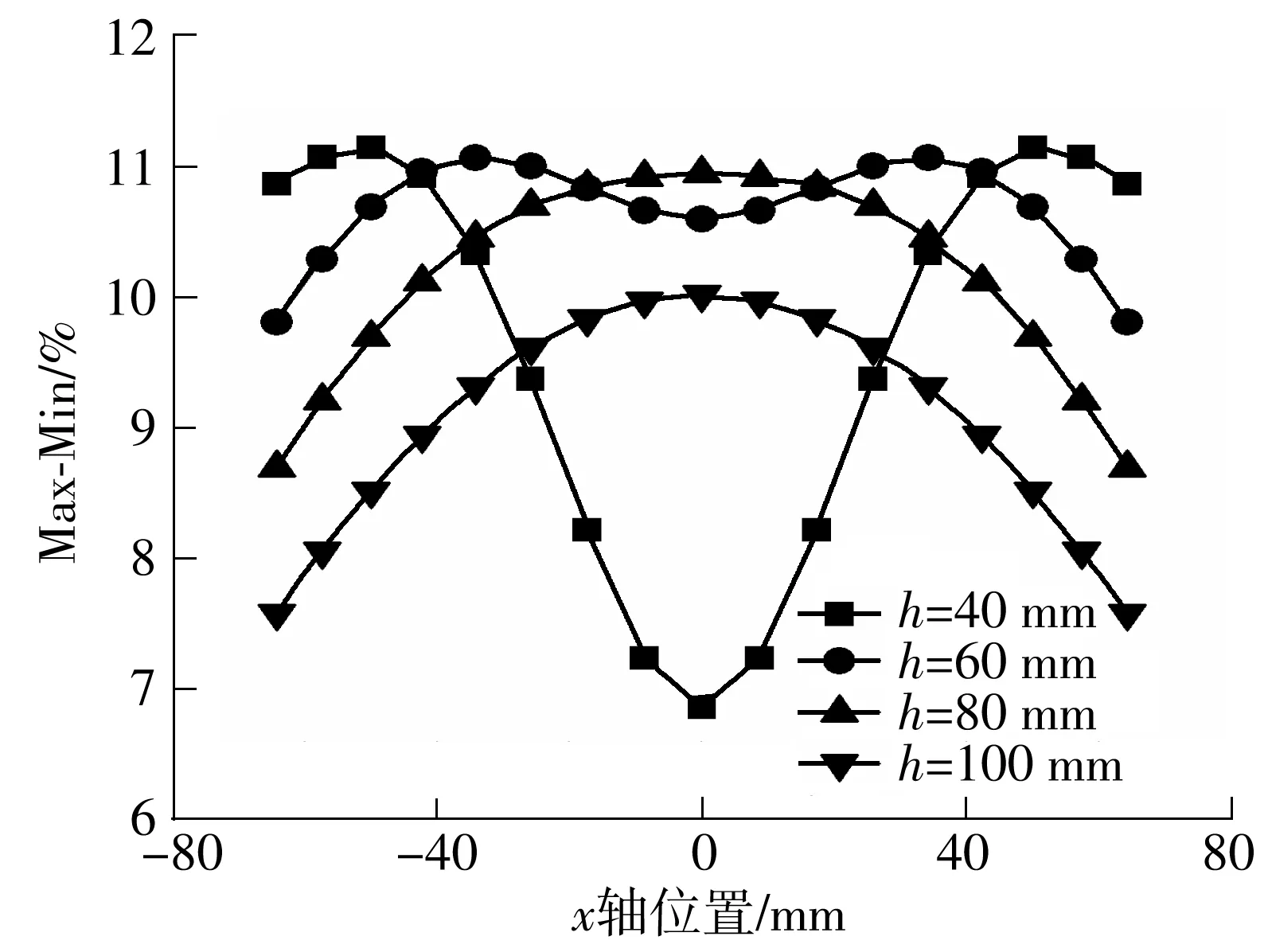
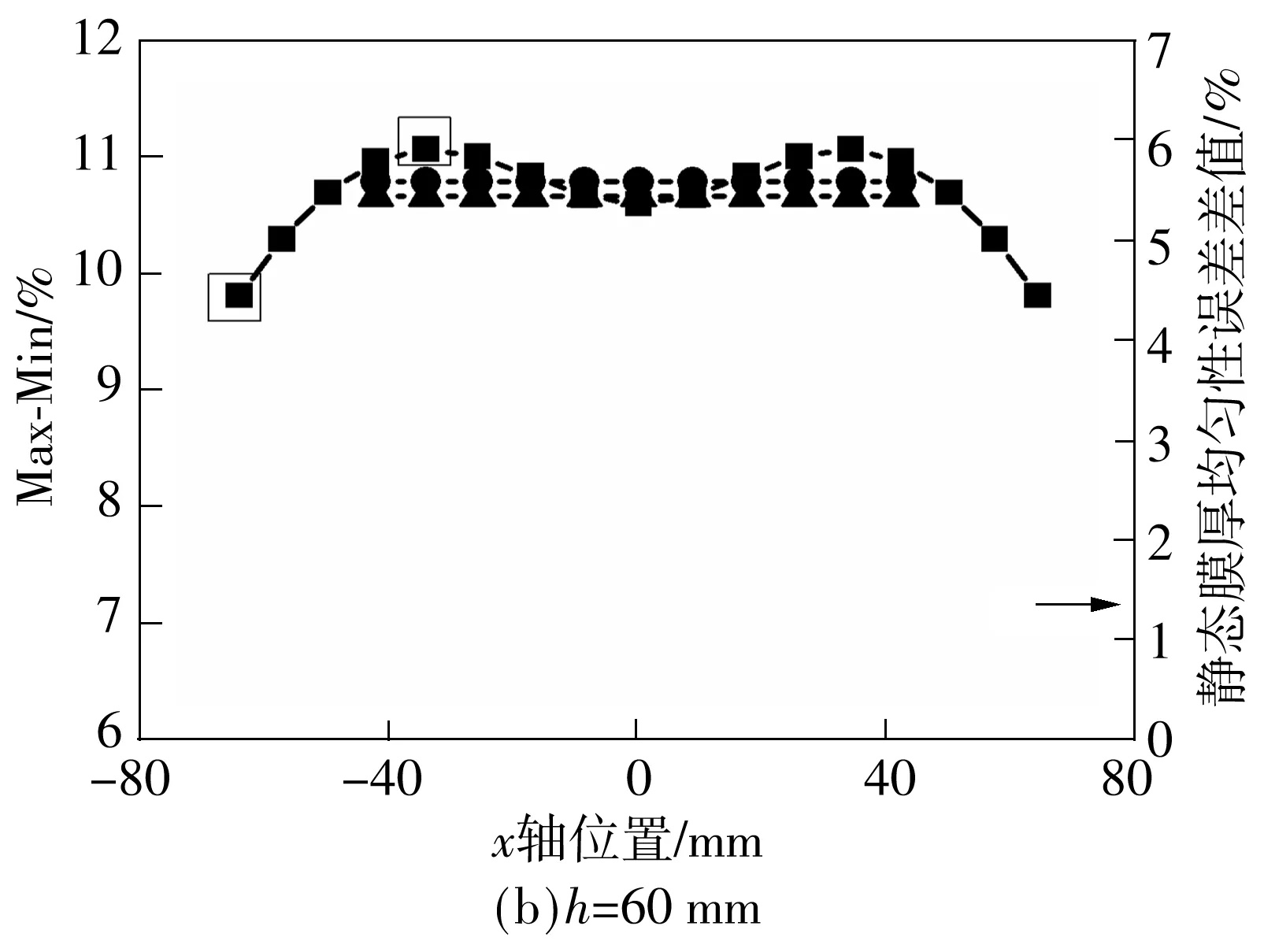
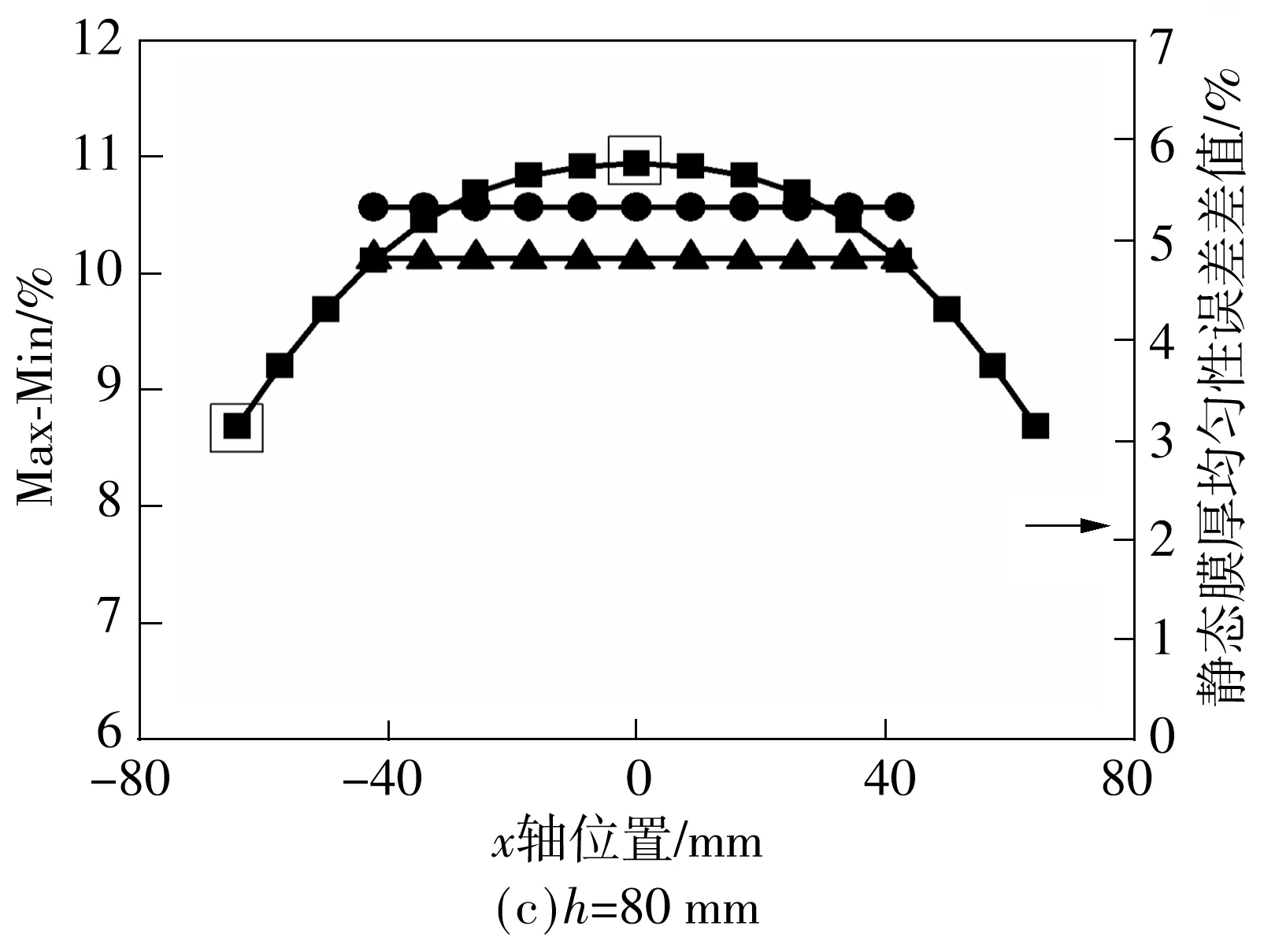
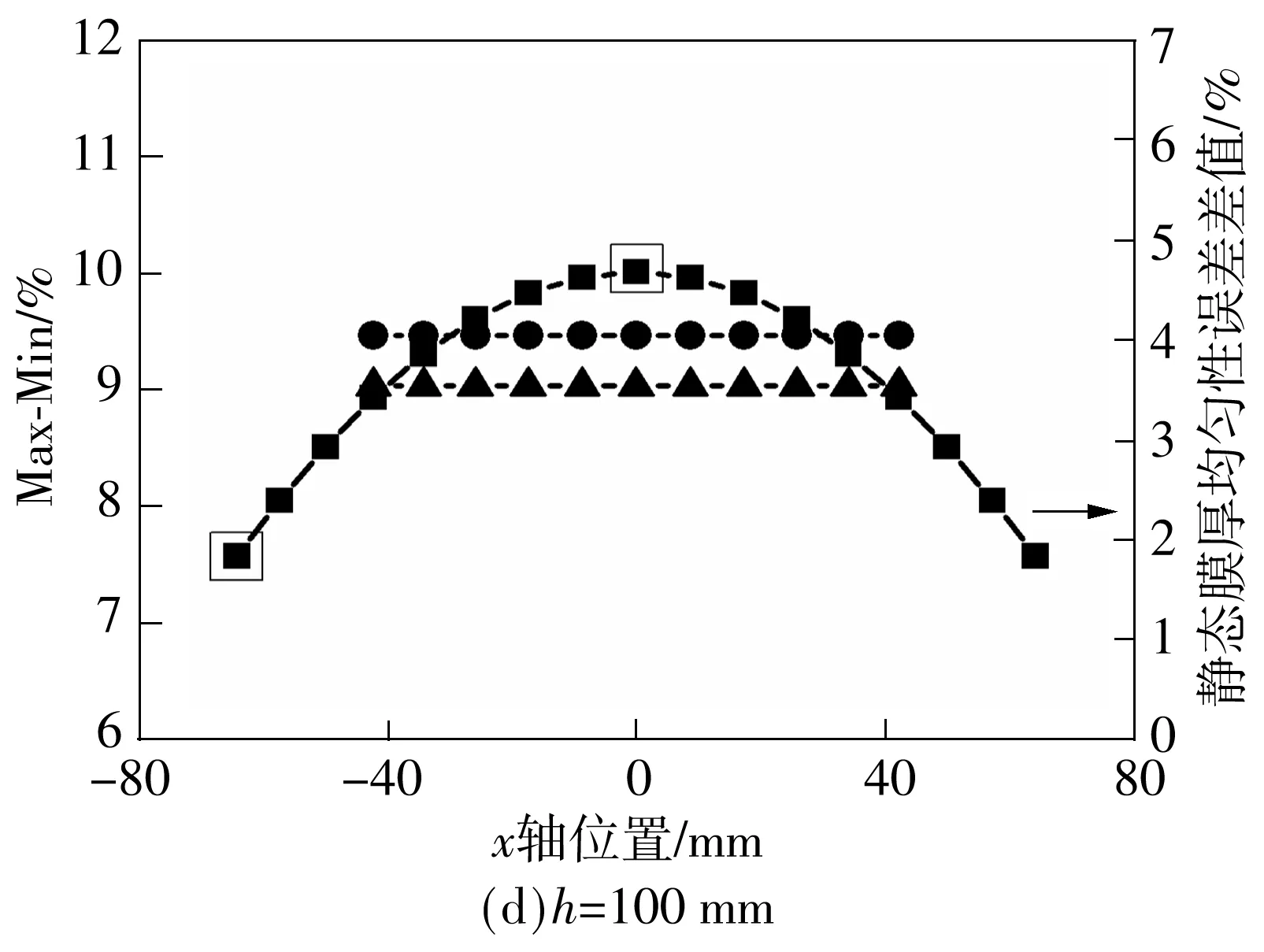
图3给出了溅射沉积范围受到矩形靶几何形状约束的示意图.当沉积角θ为90°时,表面沉积厚度为零,这意味着待沉积基片表面不在沉积范围之内.因此,根据矩形靶和弯曲基片的特点,使实际矩形靶宽度小于最大理论矩形靶宽度,即在S (1)聚焦课堂。引导教师在教学中体现“尊重之道、引导之法、激发之术”,积极推进课堂改革的四个“化”:一是国家课程校本化。允许、鼓励教师结合实际对国家课程进行校本化处理,如整合教学内容、调整模块顺序、自编学习教材、创新教学方式。二是课程开发学科化。引导教师在教学中关注课程内容的纵向拓展和横向整合,关注对学生的生涯指导和知识的学以致用。三是优质课堂多元化。鼓励教师不拘泥于固有教学模式,积极探索基于信息技术的多元互动课堂,着力构建问题导向、高阶思维的高效课堂。四是分层教学个性化。学校率先在广州市探索高中分层走班教学改革,根据学生的学习层次和认知水平实施个性化分层教学。 (9) 图3 卷对卷矩形靶的溅射范围示意图 Fig.3 Schematic diagram of sputtering scope of roll-to-roll rectangular target 从图4所示卷绕溅射的膜厚分布示意图可以看到,将弯曲基片平铺后即是平面基片,基片上的膜厚分布以网格为基础.溅射时,主辊不旋转即静态,每一个网格的厚度由Tm,n表示.主辊旋转时即为动态,薄膜厚度可由静态下沿着旋转路径(横向)分布的膜厚叠加,即由静态下沿旋转路径的网格所代表的膜厚叠加.动态下的单位膜厚Tall(i,n)可由式(10)表示: 图4 基于网格的基片膜厚分布示意图 Fig.4 Schematic diagram of thickness distribution based on grid Tall(i,n)=Ti,1+Ti,2+Ti,3+…+Ti,n-1+Ti,n= (10) 膜厚均匀性误差可以通过如下典型的Max-Min公式表征[5]: Max-Min=(Tmax-Tmin)/(Tmax+Tmin)×100%. 式中,Tmax和Tmin分别为纵向分布网格上所表示的膜厚的最大值和最小值. 3.1 静态膜厚均匀性 3.1.1 不同靶材侵蚀区长度下的静态膜厚均匀性 图5给出了靶材侵蚀区长度(靶长)L变化时膜厚分布的模拟结果.当靶基距固定时,膜厚会随着侵蚀区长度的增加而增大,说明扩大靶材侵蚀区长度(即扩大侵蚀区的总面积)时,离子轰击作用下将产生更多的沉积粒子,增加单位时间内的膜厚.此外,仿真实验还发现,中间纵向分布的膜厚增加较为明显,呈现由圆形向椭圆形,直至类矩形的转变. 图5 不同靶长下的静态膜厚分布 Fig.5 Static thickness distribution of the target with different lengths 图6给出了靶材侵蚀区长度L变化下膜厚均匀性误差的分布情况.当侵蚀区长度相对于基片在50~125 mm的范围内变化时,膜厚均匀性误差相应地呈降低的趋势,说明膜厚在纵向分布的误差会随着侵蚀区长度的增大而减小.此外,当L=125 mm时,横向分布的膜厚均匀性误差之间的整体偏差相对于其余3种条件下更小. 图6 不同靶长下的静态膜厚均匀性误差分布 Fig.6 Static thickness uniformity error distribution of the target with different lengths 由以上分析可知,通过增加侵蚀区长度,一方面可使矩形靶溅射的膜厚呈类矩形分布,有利于减小纵向膜厚误差;另一方面,当侵蚀区长度扩大到一定的值时,横向分布的膜厚均匀性误差的偏差也出现了减小的情况,这有利于减小横向叠加的累计误差,为由静态膜厚所叠加而成的动态膜厚的均匀性误差的减小提供有利条件.但靶材侵蚀区长度过长不利于材料的节约,应根据薄膜用途及品质要求设定膜厚均匀性误差阈值,对靶材几何尺寸加以控制. 3.1.2 不同靶基距下的静态膜厚均匀性 图7给出了靶基距h变化下膜厚分布的模拟结果.当靶材尺寸固定时,膜厚会随着靶基距的增大而降低.这说明增大靶基距实际上是延长了沉积粒子的运动路径,延长了沉积时间,造成单位时间内膜厚的减小.这与基于平面基片矩形靶的膜厚分布的仿真实验结果相符合[6].此外,在仿真实验中还发现,中间纵向分布的膜厚减小较为明显,由类矩形向椭圆形转变. 图7 不同靶基距下的静态膜厚分布 Fig.7 Static thickness distribution of the target in different target-to-substrate distances 图8给出了不同靶基距下膜厚均匀性误差的分布情况.当基片相对于靶位在40~100 mm的距离范围内移动时,中部的膜厚均匀性误差先升高后降低,这与基于平面基片的仿真实验结果是一致的[3].但不同的是,在卷绕系统中,左右两边缘的膜厚均匀性误差一直减小.这可能是因为弯曲基片在靶基距的变化过程中涉及到了弯曲角的问题,而平面基片不存在弯曲角,因此,当h=40 mm时,距弯曲边界较远的矩形靶侵蚀区上的面微元与该边界之间的距离已经超过了一定的范围,不像中部的膜厚均匀性误差那样会随靶基距在一定的范围内增加直至一定值时才开始减小.这说明膜厚均匀性误差的变化规律是由靶材几何尺寸与靶基距共同决定的,也说明不同维度的系统所呈现的膜厚均匀性误差的变化规律会有所不同. 图8 不同靶基距下的静态膜厚均匀性误差分布 Fig.8 Static thickness uniformity error distribution of the target in different target-to-substrate distances 综上所述,静态膜厚均匀性误差和静态膜厚均匀性误差在横向分布上的偏差均受到靶材几何尺寸和靶基距的影响,可见膜厚均匀性对靶材几何尺寸和靶基距较为敏感. 3.2 动态膜厚均匀性 动态膜厚由沿旋转方向分布的静态膜厚微元叠加而成.从图5和7可以看出,沿纵向分布的静态膜厚是不相等的;而从图6和8可以看出,沿旋转(横向)方向分布的静态膜厚均匀性误差也是不相等的,这都必然会影响动态膜厚均匀性.因此,可考虑通过对静态膜厚均匀性误差分布的控制,来减少其对动态膜厚均匀性的影响. 图9给出了不同靶基距下的动态膜厚均匀性误差、静态膜厚均匀性误差(Max-Min)分布曲线和该曲线上各参考点均值的分布.仿真实验结果表明,当靶材尺寸固定时,随着靶基距的增大,静态膜厚均匀性误差各参考点的均值先增大后减小,而这一规律与动态膜厚均匀性误差的变化规律相符,说明静态膜厚均匀性误差各参考点的均值对动态膜厚均匀性误差有着较大的影响,改变静态膜厚均匀性误差可以间接地改变动态膜厚均匀性误差.此外,当h=40 mm时,相对于其他3种条件,静态膜厚均匀性误差在横向分布的偏差较大,约为4.4%,但动态膜厚均匀性误差的却很小,约为8.3%.因此,静态膜厚均匀性误差在横向分布上的较小偏差不能说明动态膜厚均匀性也很小.另外,仿真实验结果表明,动态膜厚均匀性误差位于静态膜厚均匀性误差分布曲线的中部极值点与该分布曲线上的参考点均值之间,因此,借助卷绕溅射理论模型,有规律地改变靶材几何尺寸和靶基距来对静态膜厚均匀性误差分布进行分析,可以较快地预测动态膜厚均匀性误差的范围,进而缩短膜厚均匀性实验调试的周期. 图9 不同靶基距下的动态膜厚均匀性误差、静态膜厚均匀性误差(Max-Min)分布曲线和该曲线上各参考点的均值 Fig.9 Distribution profiles of dynamic thickness uniformity error and static thickness uniformity error (Max-Min) as well as the average value of reference point on Max-Min distribution profile of static error in different target-to-substrate distances 文中建立了一个基于卷对卷矩形靶的溅射理论模型,通过Matlab仿真,分析了靶材几何尺寸和靶基距对静态、动态膜厚均匀性的影响,仿真实验结果表明:(1)静态膜厚均匀性误差会随着靶材侵蚀区面积的增大而减小;(2)随着靶基距的增大,中部的静态膜厚均匀性误差先升高再降低,两边缘的静态膜厚均匀性误差则一直减小;(3)静态膜厚均匀性对动态膜厚均匀性有着较大的影响,控制静态膜厚均匀性可以间接控制动态膜厚均匀性;(4)动态膜厚均匀性误差位于静态膜厚均匀性误差Max-Min分布曲线的中部极值点与该分布曲线上的参考点均值之间.通过该模型的仿真,可以有效地预测动态膜厚均匀性误差的范围,缩短膜厚均匀性调试的时间.该研究结果适用于其他维度的卷对卷矩形靶的磁控溅射系统仿真. [1] Du X S,Jiang Y D,Yu J S,et al.Quantitative evaluation of film thickness uniformity:application to off-axis magnetron source onto a rotating substrate [J].Journal of Va-cuum Science and Technology,2007,25(2):215- 220. [2] Swann S,Collett S A,Scarlett I R.Film thickness distribution control with off-axis circular magnetron sources onto rotating substrate holders:comparison of computer simulation with practical results [J].Journal of Vacuum Science and Technology,1990,8(3):1299- 1303. [3] Zhang Yichen,Song Qingzhu,Sun Zhulai.Research on thin film thickness uniformity for deposition of rectangular planar sputtering target [J].Physics Procedia,2012,32:903- 913. [4] Jiang C Z,Zhu J Q,Han J C,et al.Uniform film in large areas deposited by magnetron sputtering with a small target [J].Surface and Coatings Technology,2013,229(9):222- 225. [5] Fu Chunlin,Yang Chuanren,Han Leigang,et al.The thickness uniformity of films deposited by magnetron sputtering with rotation and revolution [J].Surface and Coatings Technology,2006,200(12):3687- 3689. [6] Fan Qi-hua,Chen Xiao-hong,Zhang Ying.Computer si-mulation of film thickness distribution in symmetrical magnet magnetron sputtering [J].Vacuum,1995,46(3):229- 232. [7] Choa Sung-Hoon,Cho Chung-Ki,Hwang Woo-Jin,et al.Mechanical integrity of flexible InZnO/Ag/InZnO multilayer electrodes grown by continuous roll-to-roll sputtering [J].Solar Energy Materials and Solar Cells,2011,95(12):3442- 3449. [8] Yamada T,Ishihara M,Hasegawa M.Large area coating of graphene at low temperature using a roll-to-roll microwave plasma chemical vapor deposition [J].Thin Solid Films,2013,532(4):89- 93. [9] Tamagaki H,Ikari Y,Ohba N.Roll-to-roll sputter deposition on flexible glass substrates [J].Surface and Coatings Technology,2014,241(2):138- 141. [10] Meng X Q,Fan X J,Guo H X.A new formula on the thickness of flms deposited by planar and cylindrical magnetron sputtering [J].Thin Solid Films,1998,335(1):279- 283. [11] MacLeod H A.Thin-film optical filters [M].London:DP Publishing,2001:488- 492. [12] 徐均琪,易红伟,蔡长龙,等.磁控溅射膜厚均匀性与靶-基距关系的研究 [J] 真空,2004,41(2):25- 28. Xu Jun-qi,Yi Hong-wei,Cai Chang-long,et al.Relationship between target-substrate distance and thickness uniformity of films deposited by magnetron sputtering [J].Vacuum,2004,41(2):25- 28. [13] 张以枕.真空镀膜设备 [M].北京:冶金工业出版社,2009:102- 110. Thickness Uniformity Control of Sputtered Film Based on Roll-to-Roll System with a Rectangular Target HuangYun-xiang1WenWan-yu1SunJia-wei1HuaiChuang-feng1ZengHai-feng2ZhongFu-hui2 (1.Key Laboratory for Surface Functional Structure Manufacturing,South China University of Technology,Guangzhou 510640,Guangdong,China;2.Yangjiang Henergy Industrial Co.,Ltd.,Centre of Fabrication and Promotion for CIGSSolar Cells,Yangjiang 529533,Guangdong,China) In this paper, a sputtered theoretical model is proposed on the basis of the roll-to-roll system with a rectangular target, and with the help of the simulation software Matlab, it is used to analyze the film thickness unifor-mity of the rolled flexible substrate, whose width is 100 mm with a bending radius of 100 mm and a bending angle of 80°. First, in the stillness of main roller, the situation of the film thickness uniformity error is investigated by adjusting the geometry size of target and the substrate-to-target distance. The results show that the film thickness uniformity error as a whole decreases with the increase of the geometry size of target, and that as the substrate-to-target distance increases, the middle parts of the film thickness uniformity error first increase and then decrease, while both sides of the film thickness uniformity error decrease. Next, in the rolling condition, the distribution of the film thickness uniformity error is discussed by adjusting the substrate-to-target distance and keeping a constant geometry size of target. It is found that the film thickness uniformity error first increase and then decrease as the substrate-to-target distance increases. Simulaiton results also show that the rolling film thickness uniformity error locates between the middle maximum of the stilling film thickness uniformity error distribution curve Max-Min and the average of the reference points on this distribution curve. Through the simulation of the proposed model, the rolling film thickness uniformity error on the basis of the roll-to-roll system with a rectangular target can be predicted quickly and the number of debugging can be reduced significantly. rectangular target; roll-to-roll; vacuum magnetron sputtering;film thickness uniformity; simulation 2015- 04- 10 广东省战略性新兴产业核心技术攻关项目(2012A032300009);华南理工大学中央高校基本科研业务费专项资金资助项目(2014ZM0025) Foundation item: Supported by the Strategic Emerging Industry Core Technology Research Project of Guangdong Province(2012A032300009) 黄云翔(1987-),男,博士生,主要从事薄膜太阳电池、溅射镀膜、电化学沉积等的研究.E-mail: 282092874@qq.com 1000- 565X(2015)11- 0081- 06 TB 43 10.3969/j.issn.1000-565X.2015.11.012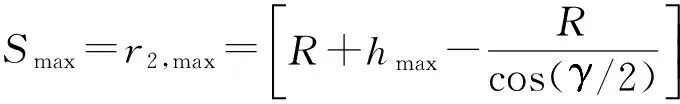
2 卷绕溅射的膜厚叠加原理
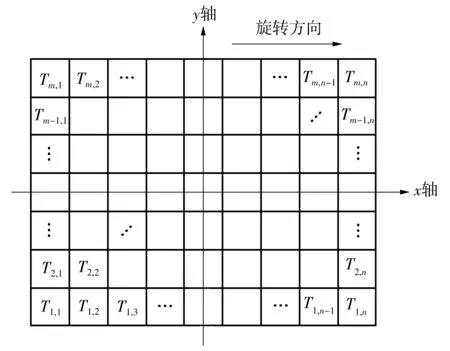
3 仿真结果及分析



4 结论

