用于网格去噪的自适应双边滤波器*

江亮亮 杨付正 任光亮

(西安电子科技大学 综合业务网理论及关键技术国家重点实验室， 陕西 西安 710071)

用于网格去噪的自适应双边滤波器*

江亮亮 杨付正 任光亮

(西安电子科技大学 综合业务网理论及关键技术国家重点实验室， 陕西 西安 710071)

为有效去除三维网格模型中的噪声,提出一种用于网格去噪的自适应双边滤波器.首先,利用体积积分不变量对三维网格模型进行特征检测,估计出局部的特征强度,然后根据特征强度自适应地调整双边滤波器的滤波参数.通过自适应的参数优化,对于不同特征强度的区域,自适应双边滤波器采用更具针对性的去噪策略,从而进一步提高了去噪性能.实验结果表明,相比于双边滤波器,所提出的自适应双边滤波器在去除噪声的同时,能够更好地保持三维网格模型的细节特征,去噪后得到的网格模型与原始模型的客观差值测度平均降低了0.033 2.

三维网格；网格去噪；双边滤波器；特征检测；特征保持

近年来,三维网格模型的应用日益广泛[1- 2].随着三维扫描技术的不断发展,三维网格模型的获取也逐渐简单和方便[3].不过,由于扫描设备精度存在误差以及其他人为因素的影响,获取的三维模型不可避免地包含了噪声信息[4- 5].噪声的存在不仅影响了三维模型的视觉质量,还不利于三维模型的压缩、简化[6]以及其他后续操作[7].因此,近年来,如何有效地去除三维网格模型中的噪声成为计算机图形学领域研究的热点之一.

去除噪声的同时保持三维网格的原始特征是网格去噪面临的最大挑战,因为噪声和边、角等尖锐的特征都是高频分量,很难有效地将它们区分开来.根据特征保持性,网格去噪方法可以分为各向同性算法和各向异性算法.早期的网格去噪方法主要是各向同性算法,这类算法在去除噪声的同时也会破坏三维网格原有的特征.Taubin[8]于1995年提出了基于Laplacian算子的网格信号处理方法,利用傅里叶变换对网格信号进行频域分析,并通过低通滤波器实现网格光顺,该方法计算复杂度低,但稳定性较差.Desbrun等[9]提出沿法向量方向更新顶点的位置,根据平均曲率确定移动的步长,并通过重采样避免滤波后网格体积发生收缩.随后,Ohtake等[10]对文献[9]中的算法进行改进,将平均曲率和Laplacian算子结合起来,减少了过度平滑情况的发生.由于各向同性这一性质,各向同性算法在平滑噪声的同时也会模糊三维网格模型原有的特征.为了更好地保持三维网格的特征,后续的研究者们提出了多种各向异性算法[11- 15].文献[11- 12]中将图像去噪中的各向异性扩散方法扩展到网格去噪中,这类算法会根据三维网格的几何特征自适应地改变扩散张量,达到保持特征的目的.不过,这类算法需要众多的微分和矩阵运算,计算复杂度较高.文献[13- 14]中将图像去噪中的双边滤波器扩展到网格去噪中,利用双边滤波器分配的权重确定顶点更新的方向和步长.Hildebrandt等[15]提出采用平均曲率流去除噪声,在滤波过程中使网格的平均曲率收敛于一个既定的平均曲率.

另外,近年来,很多研究者[16- 20]提出了一种两步法的滤波框架,首先将滤波算法作用于法向量域,调整各个面的法向量,然后根据调整后面的法向量更新网格的顶点坐标.文献[16- 17]中利用均值滤波器、中值滤波器以及alpha-Trimming滤波器对面的法向量进行滤波.文献[18]中提出利用较为复杂的模糊向量中值滤波器调整面的法向量.文献[19]中设定一个门限,选择邻域内较接近的法向量,然后通过对这些法向量进行加权平均更新面的法向量.文献[20]中将双边滤波器作用于法向量域,综合考虑了空间距离和数值差异两方面的因素,在去除噪声的同时较好地保持了三维网格的原始特征.

实验表明,将双边滤波器作用于法向量域能够有效保持三维网格的原始特征[20],对于一个三维网格模型,双边滤波器使用的是一组固定的滤波参数.然而,三维网格模型表面各局部区域的特性是不同的,在整个网格模型使用固定的滤波参数对局部区域并非最优,反而在一定程度上制约了双边滤波器的去噪性能.为此,文中提出一种基于自适应双边滤波器的网格去噪方法,在局部区域,利用特征强度驱动双边滤波器,自适应地优化双边滤波器的滤波参数,从而最大程度地发挥双边滤波器的去噪能力.由于三角形网格是三维网格模型最常见的表现形式,且已有的算法主要是针对三角形网格[14- 15,19- 20],因此,文中也主要研究三角形网格的去噪方法.

1 去噪方法的原理

文中提出的去噪方法如图1所示.其中:特征强度检测模块主要是估计三维网格模型表面各区域的平坦程度,为后续双边滤波器的自适应性提供支持;自适应双边滤波器模块主要是依据特征强度自适应地优化滤波参数,并校正各个三角形面的法向量;顶点更新模块则是根据校正后的法向量更新顶点的坐标位置.

图1 基于自适应双边滤波器的网格去噪方法框图

Fig.1 Framework of mesh denoising method based on adaptive bilateral filter

2 特征强度检测

在三维网格模型中,有的区域表面平坦,没有尖锐特征,特征强度较低;而有的区域凹凸不平,尖锐特征多,特征强度较高.在不同特征强度的区域,去噪的侧重点是不同的.对于特征强度较低的区域,去噪主要是侧重于对曲面进行光顺,而对于特征强度较高的区域,去噪主要是侧重于恢复曲面的尖锐特征.因而,在网格去噪过程中,检测局部特征强度很有必要,因为它有利于为不同特征强度的区域制定相应的滤波策略.

三维网格模型的特征提取方法主要分为两类:基于边的方法和基于面的方法.基于边的方法首先找出曲率突变的点作为边点,然后将这些边点连接成线[21];而基于面的方法以一组“种子点”为中心进行“区域增长”,找出一组具有相似特征的点构成曲面,直至周围邻域内没有特征相似的点才停止“生长”,最后根据相邻曲面相交或其他算法得到曲面边界[22].无论是基于点的方法,还是基于面的方法,都只能对三维网格模型的特征进行区分,无法获得局部区域确切的特征强度.文中以顶点为中心,通过计算顶点的体积积分不变量[23]来衡量局部特征强度.设M为输入网格,任意一点p∈M,点p的体积积分不变量定义为

Vr(p)=∫Br(p)∩IMdx

(1)

式中,Br(p)为以点p为中心、半径为r的球,IM为输入网格的内部空间,体积积分不变量Vr(p)为Br(p)和IM重叠区域的体积.从体积积分不变量的定义中可以看出,顶点的体积积分不变量与该顶点周围曲面的凹凸程度是相关的,能够反映顶点位置的特征强度.为了更加清楚地表示体积积分不变量与曲面特征强度的关系,将Vr(p)进行归一化处理:

(2)

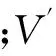
(3)

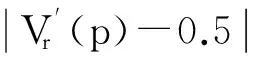
体积积分不变量的值与内核球的半径r有关,在不同尺度r下,利用体积积分不变量检测出的特征强度会存在一定的差异.为了提高特征检测的鲁棒性,文中选择多个尺度,将多个尺度下的特征强度融合,取它们的平均值作为特征强度的最终值,即

(4)

式中:S(p)为点p处的特征强度的最终值;N为尺度个数,在文中的实验中,N取为2;r1和r2分别取3la和5la,la为三维模型的平均边长.图2给出了三维模型Octa-Flower的特征强度分布图,颜色越偏暖,表示特征强度越高.图2(b)是Octa-Flower原始模型的特征强度分布图,可以看出,在平坦的区域,颜色偏冷,特征强度较低;而在边、角等具有尖锐特征的区域,颜色偏暖,特征强度较高,可见特征强度检测的结果与三维网格模型的局部特性较为一致.另外,由于特征强度检测主要是针对带噪模型的,特征强度检测方法的抗噪性也非常重要.图2(c)给出了Octa-Flower带噪模型的特征强度分布图,特征强度检测的结果与三维网格模型的局部特性也较为一致,受到噪声的影响较小,可见体积积分不变量对噪声具有较强的鲁棒性.

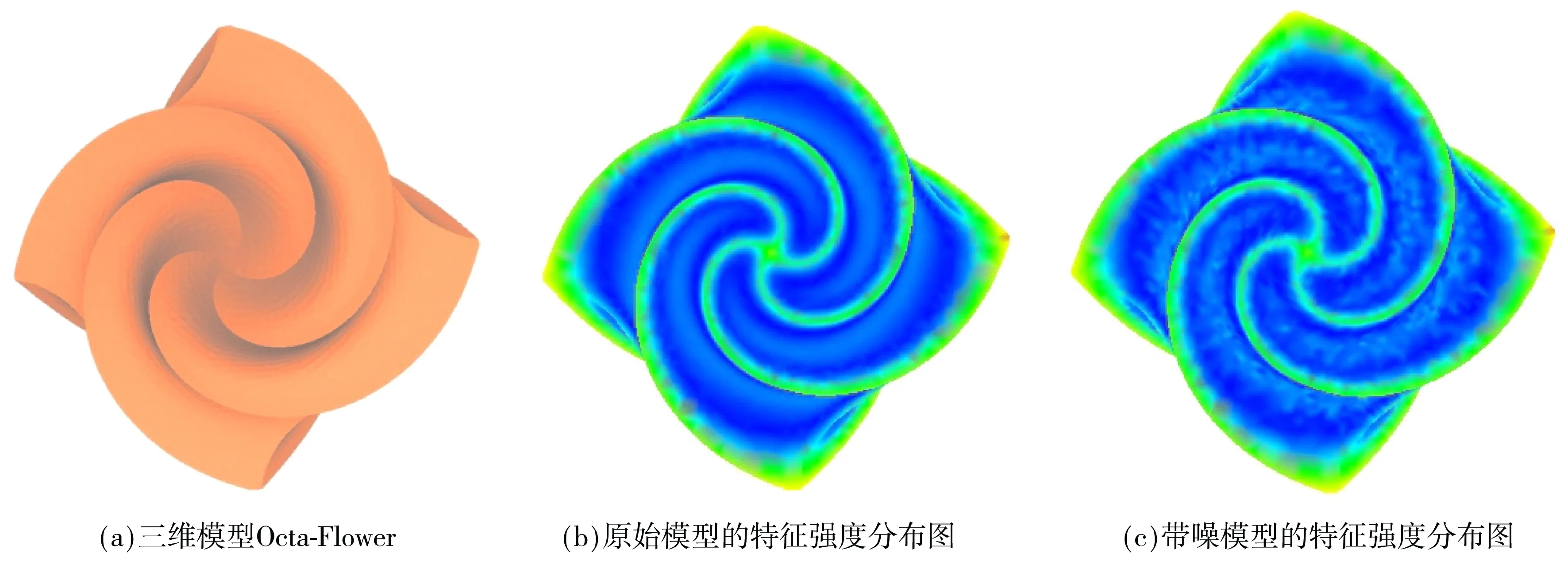
图2 三维模型Octa-Flower的特征强度分布图

由于后续的去噪方法首先要校正的是三角形面的法向量,因而需要得到各个三角形面的特征强度.在已知顶点特征强度的情况下,三角形面的特征强度可以通过对其3个顶点的特征强度取平均得到.

3 自适应双边滤波器

双边滤波器将空间相近度和数值相似度两个重要因素有效结合,能够在保持细节特征的前提下较好地去除噪声,文献[13- 14]中将该算法推广到网格模型.Zheng等[20]提出了一种双边法向滤波器,将双边滤波器作用于法向量域,取得了不错的去噪效果.在文献[20]的基础上,文中提出一种自适应双边滤波器,结合三维模型局部特征强度,自适应地优化双边滤波器的参数,进一步提高双边滤波器的去噪性能.自适应双边滤波器的法向量更新公式为

(5)

Wd(‖ci-cj‖)=exp(-‖ci-cj‖2/2δd2)

(6)

Wr(‖ni-nj‖)=exp(-‖ni-nj‖2/2δr(i)2)

(7)

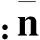
在双边滤波器中,空域滤波器和数值滤波器具有不同的功能,空域滤波器侧重于平滑和光顺,而数值滤波器侧重于保持特征.在三维模型不同特征强度的区域,去噪的侧重点也是有区别的.对于特征强度较低的区域,通过简单的平滑和光顺就能较好地完成去噪;对于特征强度较高的区域,在平滑噪声的同时还必须注意保持尖锐的特征.因此,在特征强度较低的区域,空域滤波器应该在双边滤波器中占据主导地位;而在特征强度较高的区域,数值滤波器则应该处于较为重要的位置.空域滤波器和数值滤波器在双边滤波器中所处的地位是由滤波参数δd和δr(i)共同决定的.自适应双边滤波器选择将δd的值固定,并根据局部特征强度动态调整δr(i)的值,实现局部区域空域滤波器和数值滤波器的合理搭配,最大程度地发挥双边滤波器的去噪效果.由于δd的值是固定的,随着特征强度的增大,δr(i)需相应地减小以提高数值滤波器在双边滤波器中的重要性.δr(i)的动态优化公式为

δr(i)=δ0+δ1g(S(fi))

(8)

式中:δ0(δ0>0)和δ1(δ1>0)是滤波参数;S(fi)是三角形面fi的特征强度;g(x)是单调递减函数,且g(x)∈(0,1].δ0是δr(i)的基础值,主要是防止δr(i)接近于0导致双边滤波器不稳定,这里δ0=0.1.δ1的取值与三维模型和噪声强度均有关,取值越大,滤波的结果越光滑.函数g(x)描述的是δr(i)随着S(fi)下降的趋势,在实验中将g(x)分别设为高斯下降函数和指数下降函数,结果表明指数下降函数是一个较好的选择.因此,文中将g(x)选为指数下降函数,即

(9)

式中,β是控制下降速度的参数,它通过一种自动的方式确定:利用k-均值算法将三维模型所有面的特征强度分为两类,每一类特征强度都有一个簇中心,将β设为这两个簇中心的均值.

在很多情况下,一次迭代更新并不能够完全消除噪声,通常需要利用自适应双边滤波器对法向量进行多次迭代更新.迭代的次数主要依赖于噪声的强度,噪声强度越大,迭代的次数就越多.

4 顶点更新

(10)

由于方程组(10)没有非平凡解,通常需要转化为最小二乘问题解决,即定义一个代价函数e(x),更新顶点使e(x)最小.代价函数的形式并不是唯一的,常用的有两种:

(11)

(12)

式中,Ai为三角形面fi的面积.上述最小二乘问题可以通过梯度下降、共轭梯度等多种方法进行求解.文中采用的是文献[19]中的顶点更新算法,该算法选取的代价函数为式(11),求解的方法为梯度下降法.

5 实验结果与性能分析

为了验证自适应双边滤波器的性能,挑选Octa-Flower、Twirl、Laurent-Hand和Bunny_iH4个模型进行实验,其中Octa-Flower和Twirl属于计算机构建的CAD模型,而Laurent-Hand和Bunny_iH是利用扫描数据重建的真实模型.在这4个模型上加入不同强度的高斯白噪声,高斯白噪声的强度与三维模型的平均边长la成比例,文中叠加在模型Octa-Flower和Laurent-Hand上的噪声的方差为0.05la和0.08la,叠加在模型Twirl和Bunny_iH上的噪声的方差为0.08la和0.10la.

将自适应双边滤波器(ABF)与文献[20]中的双边滤波器(BF)进行对比,自适应双边滤波器的参数包括滤波参数δ1、法向量更新的迭代次数t1以及顶点更新的迭代次数t2,即(δ1,t1,t2).双边滤波器的参数包括数值滤波器的标准差δs、法向量更新的迭代次数t1及顶点更新的迭代次数t2,即(δs,t1,t2).δ1的取值范围通常在[0.2,0.7],δs的取值范围通常在[0.2,0.6],δ1和δs的取值越大,滤波结果往往越光滑.法向量更新的迭代次数t1与噪声强度有关,一般噪声强度越大,迭代的次数就越多;顶点更新的迭代次数t2一般设为20.

网格去噪的目的是将加噪模型最大程度地恢复至原始模型,衡量去噪性能的指标就是经去噪得到的三维网格与原始三维网格的接近程度.文中首先利用三维网格质量评价方法MSDM2[24]比较去噪后得到的三维网格与原始三维网格之间的差异,差异越小,去噪的效果就越好.表1列出了各模型的实验结果,对于各个实验模型,自适应双边滤波器对应的MSDM2值均比双边滤波器的低.总的来说,相比于双边滤波器,自适应双边滤波器对应的MSDM2值平均降低了0.033 2.所以,从客观数值上看,利用自适应双边滤波器去噪得到的网格模型与原始三维网格更加接近.此外,从表1中还可以看到,对于同一实验模型,噪声强度越大,去噪后得到的网格模型与原始三维网格之间的MSDM2值往往越大,表明噪声强度越大,将加噪模型恢复成原始模型的难度就越大.

表1 实验结果对比

为更加直观地比较去噪方法的性能,图3-6给出了三维网格去噪的主观实验结果,相应的局部放大图中的虚线框表示改进较为明显的区域.图3是模型Octa-Flower的去噪结果,对比图3(c)和3(d)可以看到,BF在去噪过程中模糊了Octa-Flower模型花瓣边缘的尖锐特征,而ABF较好地保持了这方面的特征.图4是Twirl的去噪结果,在图4(c)中,三维模型的凹槽内出现了一条明显的裂纹,而在图4(d)中,这样的裂纹并不存在.通过与原始三维网格的对比发现,图4(d)中ABF的结果与原始三维网格更为接近.图5是模型Laurent-Hand的去噪结果,相比于原始三维网格中的掌纹,BF去噪结果中的掌纹过于平滑,而ABF较好地保持了掌纹的细节特征.图6是模型Bunny_iH的去噪结果,从中可以看出,BF和ABF的去噪结果都损失了一些细节特征,但相比于BF,ABF保留的细节特征更多.综上所述,无论是从客观数值评价指标,还是从重建三维网格的视觉效果来看,ABF的去噪效果都要优于BF.

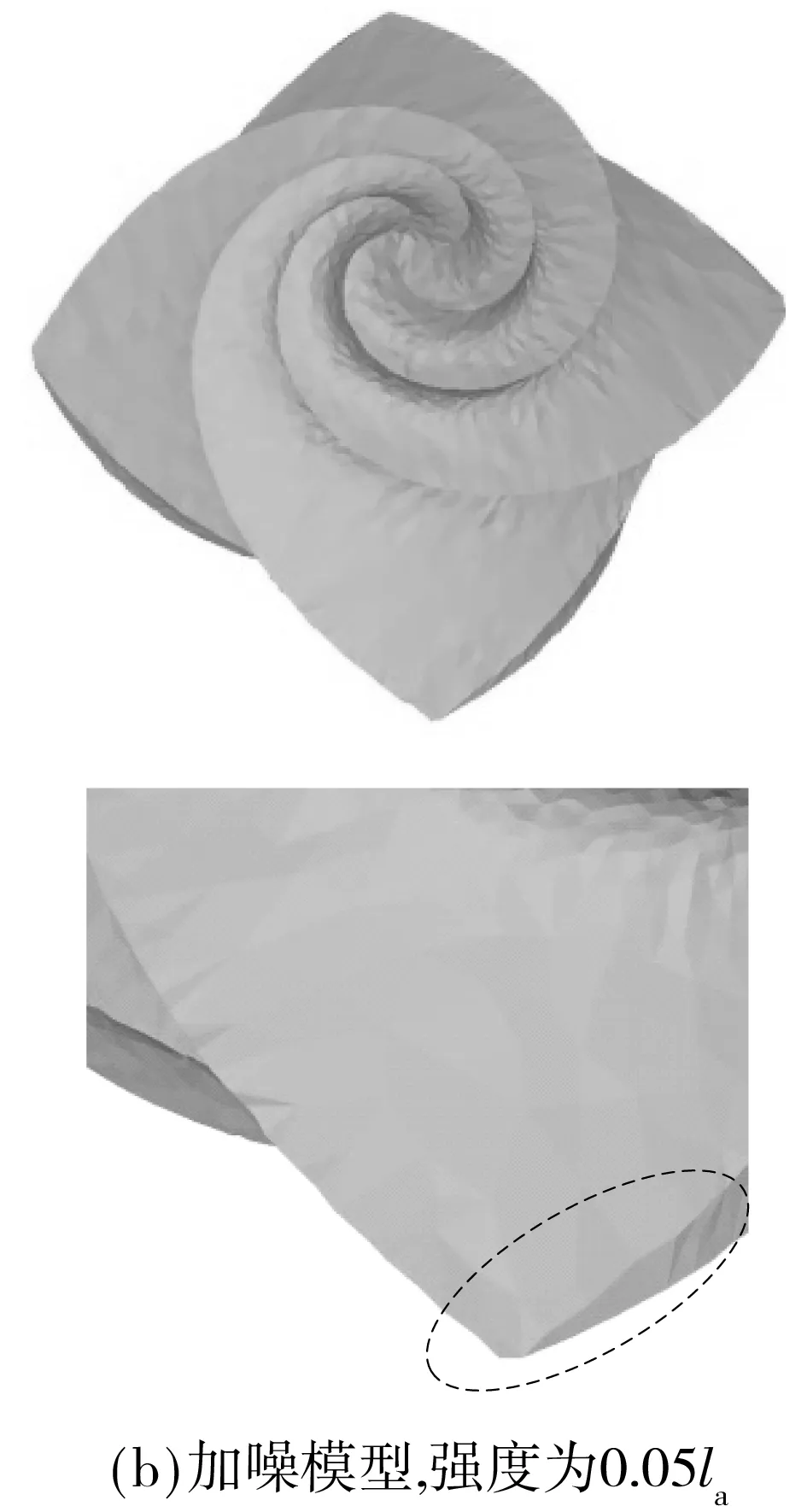
图3 模型Octa-Flower的去噪结果

图4 模型Twirl的去噪结果

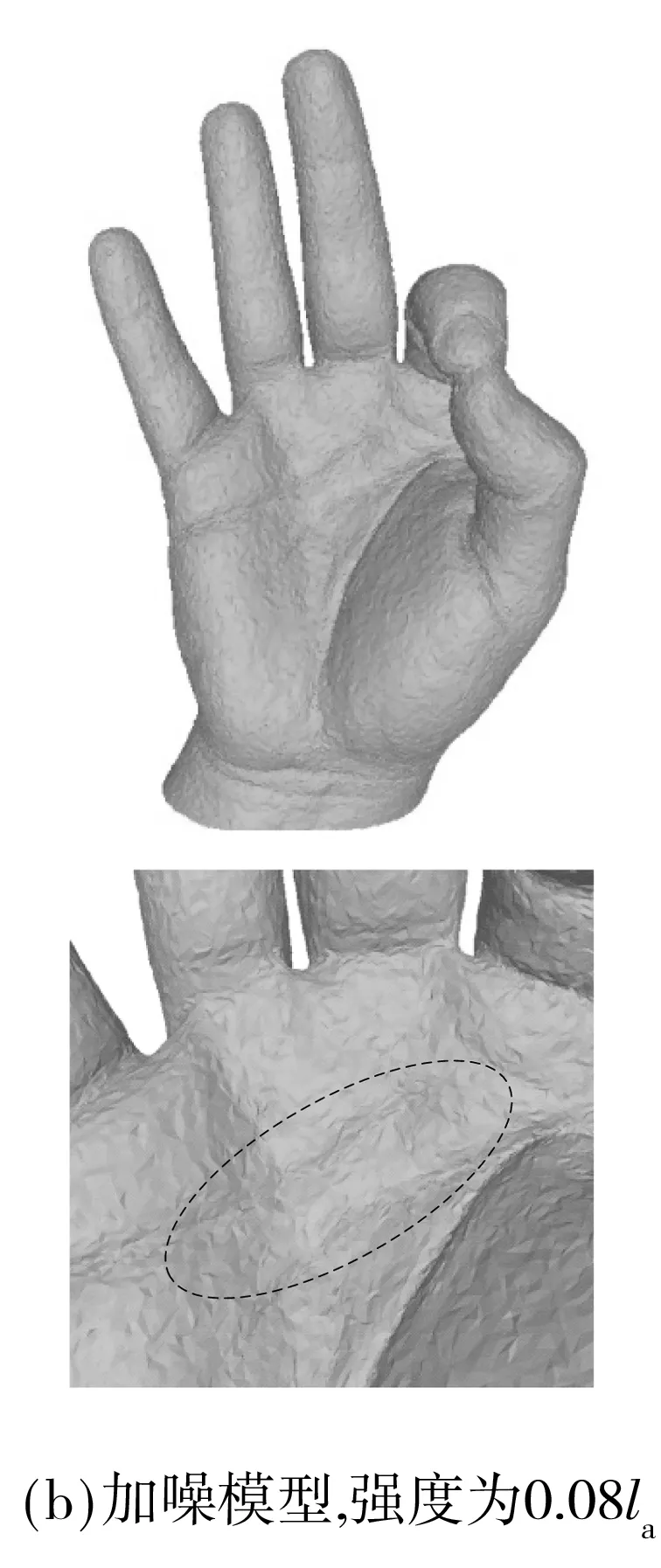
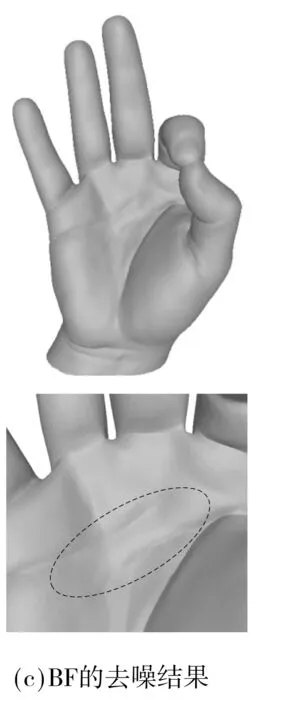
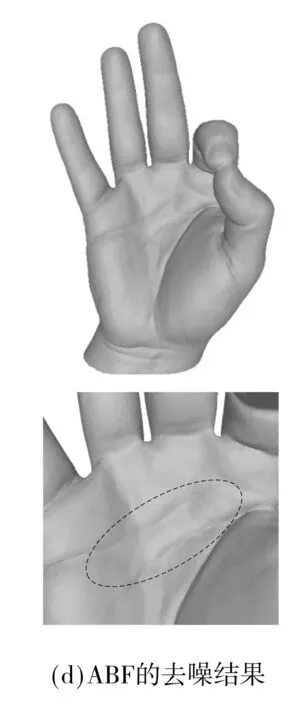
图5 模型Laurent-Hand的去噪结果

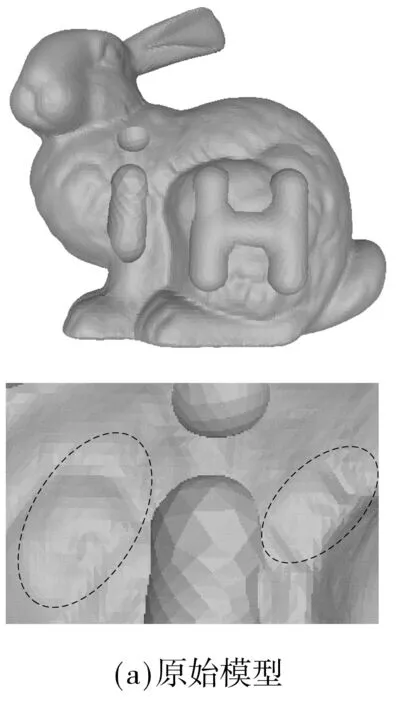
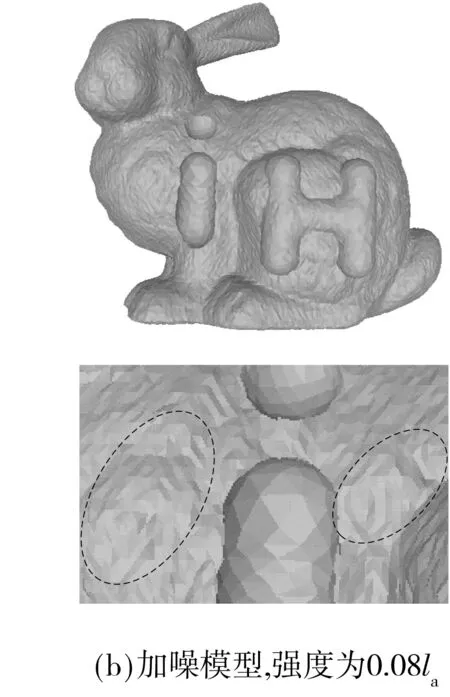
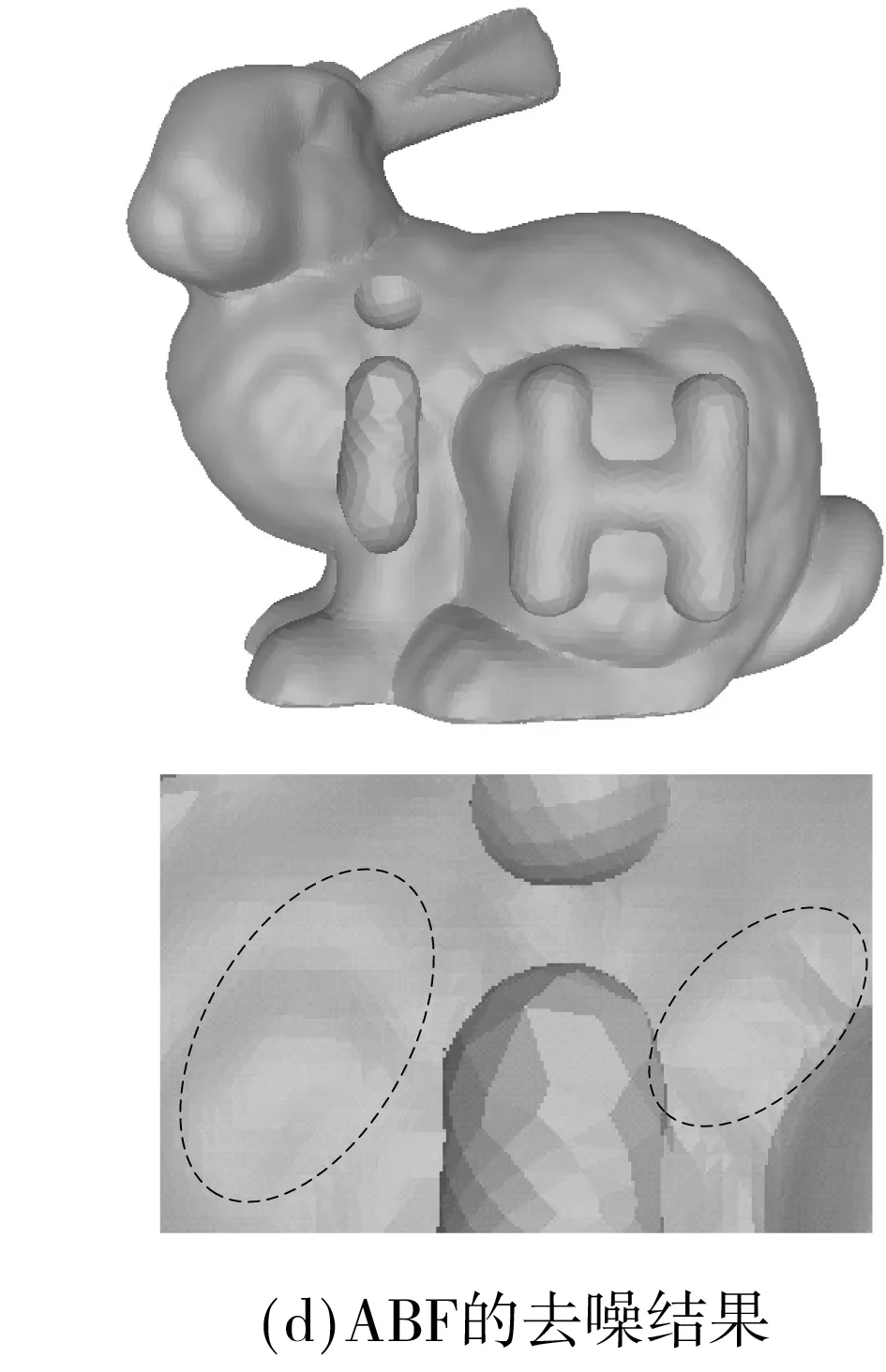
图6 模型Bunny_iH的去噪结果

不过,相比于双边滤波器,自适应双边滤波器需要进行特征强度检测,增加了一定的复杂度.表1列出了BF和ABF运行所耗费的时间,计算机配置为四核Intel Core i3-3240,主频3.4 GHz,内存4 GB.从表1中可以看出,由于特征强度检测模块较高的复杂度,ABF所花费的时间明显大于BF.然而,网格去噪的应用场景多为非实时场景,对计算复杂度的要求并不高,所以,ABF耗时虽然较长,但仍具有较大的应用价值.

6 结语

三维扫描仪本身存在的误差以及人为的扰动会导致获取的三维模型包含或多或少的噪声,三维网格去噪是提升三维模型质量的重要手段.文中提出一种用于网格去噪的自适应双边滤波器,结合三维网格模型的局部特征强度,自适应地优化滤波参数,实现局部双边滤波器中数值滤波器和空域滤波器的合理搭配.实验结果表明,相比于双边滤波器,自适应双边滤波器在去除噪声的同时,能够更好地保持三维网格模型的细节特征.不过,自适应双边滤波器检测特征强度的复杂度较高,在下一步的研究中,需要在保持特征强度检测准确性的前提下,有效地降低特征强度检测算法的复杂度.

[1] Maglo A,Lavou G,Dupont F,et al.3D mesh compression:survey,comparisons,and emerging trends [J].ACM Computing Surveys,2015,47(3):44/1- 41.

[2] 黄炎生,郑华彬,蔡健.三维场景体系在建筑结构上的应用 [J].华南理工大学学报:自然科学版,2004,32(2):54- 57. Huang Yan-sheng,Zheng Hua-bin,Cai Jian.Application of three dimension scene system in building structures [J].Journal of South China University of Technology:Natural Science Edition,2004,32(2):54- 57.

[3] Cong P,Xiong Z,Zhang Y,et al.Dense single-shot 3D scanning via stereoscopic fringe analysis [C]∥Proceedings of the IEEE International Conference on Image Processing.Melbourne:IEEE,2013:3627- 3631.

[4] Wang X,Liu X,Qin H.Robust surface consolidation of scanned thick point clouds [C]∥Proceedings of the International Conference on Computer-Aided Design and Computer Graphics.Hong Kong:IEEE Computer Society,2013:38- 43.

[5] Lin S,Wen C.Preproessing and modeling for visual-based 3D indoor scene reconstruction [C]∥Proceedings of the 8th International Conference on Computer Science and Education.Colombo:IEEE Computer Society,2013:1324- 1328.

[6] 孙殿柱,李心成,范志先,等.采用R*-tree的三角网格曲面非均匀精简算法 [J].西安交通大学学报,2008,42(9):1179- 1183. Sun Dian-zhu,Li Xin-cheng,Fan Zhi-xian,et al.Simplified algorithm for triangular mesh surface based on R*-tree [J].Journal of Xi’an Jiaotong University,2008,42(9):1179- 1183.

[7] Zhu L,Wei M,Yu J,et al.Coarse-to-fine normal filtering for feature-preserving mesh denoising based on isotropic subneighborhoods [J].Computer Graphics Forum,2013,32(7):371- 380.

[8] Taubin G.A signal processing approach to fair surface design [C]∥Proceedings of the ACM SIGGRAPH Confe-rence on Computer Graphics.Los Angeles:ACM,1995:351- 358.

[9] Desbrun M,Meyer M,Schroder P,et al.Implicit fairing of irregular meshes using diffusion and curvature flow [C]∥Proceedings of the ACM SIGGRAPH Conference on Computer Graphics.Los Angeles:ACM,1999:317- 324.

[10] Ohtake Y,Belyaev A G,Bogaevski I A.Mesh regularization and adaptive smoothing [J].Computer-Aided Design,2001,33(11):789-800.

[11] Bajaj C,Xu G.Anisotropic diffusion on surfaces and functions on surfaces [J].ACM Transaction on Gra-phics,2003,22(1):4- 32.

[12] Ouafdi A E,Ziou D.A global physical method for manifold smoothing [C]∥Proceedings of the IEEE International Conference on Shape Modeling and Applications.Stony Brook:IEEE,2008:11- 17.

[13] Fleishman S,Drori I,Cohen-Or D.Bilateral mesh denoi-sing [J].ACM Transaction on Graphics,2003,22(3):950- 953.

[14] Jones T R,Durand F,Desbrun M.Non-iterative feature-preserving mesh smoothing [J].ACM Transaction on Graphics,2003,22(3):943- 949.

[15] Hildebrandt K,Polthier K.Anisotropic filtering of non-linear surface features [J].Computer Graphics Forum,2004,23(3):391- 400.

[16] Yagou H,Ohtake Y,Belyaev A.Mesh smoothing via mean and median filtering applied to face normals [C]∥Proceedings of the International Conference on Geometric Modeling and Processing.Wako:IEEE Computer Society,2002:124- 131.

[17] Yagou H,Ohtake Y,Belyaev A.Mesh denoising via iterative alpha-trimming and nonlinear diffusion of normals with automatic thresholding [C]∥Proceedings of Computer Graphics International.Tokyo:IEEE Computer Society,2003:28- 33.

[18] Shen Y,Barner K E.Fuzzy vector median-based surface smoothing [J].IEEE Transaction on Visualization and Computer Graphics,2004,10(3):252- 265.

[19] Sun X,Rosin P L,Martin R R,et al.Fast and effective feature-preserving mesh denoising [J].IEEE Transaction on Visualization and Computer Graphics,2007,13(5):925- 938.

[20] Zheng Y,Fu H,Au O K-C,et al.Bilateral normal filtering for mesh denoising [J].IEEE Transaction on Vi-sualization and Computer Graphics,2011,17(10):1521- 1530.

[21] Yang M,Lee E.Segmentation of measured point data using a parametric quadric surface approximation [J].Computer-Aided Design,1999,31(7):449- 457.

[22] Chen Y H,Liu C Y.Quadric surface extraction using genetic algorithms [J].Computer-Aided Design,1999,31(2):101- 110.

[23] Pottmann H,Wallner J,Huang Q,et al.Integral inva-riants for robust geometry processing [J].Computer Aided Geometric Design,2009,26(1):37- 60.

[24] Lavoué G.A multiscale metric for 3d mesh visual quality assessment [J].Computer Graphics Forum,2011,30(5):1427- 1437.

Adaptive Bilateral Filter for Mesh Denoising

JiangLiang-liangYangFu-zhengRenGuang-liang

(State Key Laboratory of Integrated Services Networks，Xidian University，Xi’an 710071，Shaanxi，China)

In this paper, an adaptive bilateral filter is proposed to remove noises in 3D mesh models. Firstly, the feature detection of 3D mesh models is performed on the basis of the volume integral invariant, and the local feature strength is estimated. Then, the proposed filter adaptively adjusts the denoising parameters in the bilateral filter according to the local feature strength. Through the adaptive optimization of parameters, the proposed filter provides targeted denoising strategies for the regions with different feature strength, thus further improving the denoising performance. Experimental results reveal that, in comparison with common bilateral filters, the proposed adaptive bilateral filter achieves a superior performance in preserving the sharp features of 3D mesh models during the denoising, and the objective distance measure between the denoised mesh model and the original model is averagely reduced by 0.033 2.

3D meshes; mesh denoising; bilateral filter; feature detection; feature preserving

2015- 04- 07

国家自然科学基金资助项目(61371089,61571337) Foundation items: Supported by the National Natural Science Foundation of China(61371089,61571337)

江亮亮(1988-),男,博士生,主要从事三维模型去噪及质量评估技术研究.E-mail: lljiang@stu.xidian.edu.cn

1000- 565X(2015)11- 0054- 07

TP391

10.3969/j.issn.1000-565X.2015.11.008