平流铸造Fe78Si9B13非晶合金薄带流动与传热的数值模拟*
孙海波 李烈军,2
(1.华南理工大学 机械与汽车工程学院, 广东 广州 510640; 2.广东韶关市华工高新技术产业研究院, 广东 韶关 512000)
平流铸造Fe78Si9B13非晶合金薄带流动与传热的数值模拟*
孙海波1李烈军1,2
(1.华南理工大学 机械与汽车工程学院, 广东 广州 510640; 2.广东韶关市华工高新技术产业研究院, 广东 韶关 512000)
基于二维非稳态传热-多相流耦合模型和三维非稳态单辊结晶器传热模型,结合生产数据,对平流铸造Fe78Si9B13时熔潭形成过程中的流动、传热现象以及结晶器内的传热特征进行了研究.结果表明:在文中工艺条件下,熔潭稳定形成后,其上游弯月面呈C形,下游弯月面呈带波纹的斜坡状;结晶器达到热平衡状态的时间为20 s;高温熔体对结晶器冲击后,会在距表面0.000 4 m范围内形成一个热冲击区,该区域表面中心最高温度可达513.5 K;与径向热膨胀相比,结晶器周向热膨胀对实际总膨胀量的贡献更大,约为96%.
平流铸造;非晶合金;流动;传热;数值模拟
平流铸造工艺是生产具有优异物理和机械性能的铁基或铁镍基纳米晶、非晶合金薄带等功能磁性材料的重要的快速凝固技术之一.该工艺中,熔潭形成过程及熔潭内熔体的流动、传热行为直接决定着单辊结晶器的热和变形行为,从而严重影响非晶合金薄带产品的尺寸精度及质量提升.
由于液态金属凝固时间短,熔池尺寸小,且铜辊转速快,采用试验手段难以对平流铸造过程中的物理现象进行深入、细致的研究[1- 2].为此,前人开发和建立了基于润滑理论的低Reynold数模型[3]、二维稳态N-S模型[4- 5]、SOLA-VOF模型[6- 7]及VOF模型[8- 9],以研究平流铸造中熔潭的形成过程及熔潭内部的流动和传热行为.然而,上述模型中,多引入熔潭/结晶器界面理论换热系数[10- 11]对熔潭内熔体的传热和相变行为进行研究,易引起误差.此外,对于直接影响单辊结晶器表面膨胀行为的结晶器内部热状态的研究亦鲜见报道[12- 13].
有鉴于此,文中首先将熔潭和结晶器作为一个整体研究区域,建立了考虑自由液面形状变化和结晶器高速旋转行为的二维非稳态传热-多相流耦合模型,对熔潭形成过程中的流动、传热行为及熔潭形状特征进行了描述和分析.然后,结合生产过程中的数据,在对达到热平衡状态的单辊结晶器热边界条件进行定量描述的基础上,建立了三维非稳态单辊结晶器传热模型,进而对影响结晶器变形行为的热状态进行分析和研究,以期为平流铸造工艺优化提供理论依据.
1 熔潭模型的建立
1.1 基本假设
平流铸造工艺过程如图1所示.为准确、有效地分析平流铸造过程中的非稳态流动和传热现象,模型作如下假设[12,14]:
(1)空气与高温液态金属均为不可压缩流体;
(2)考虑到辊嘴间距较小(约0.000 3 m),熔潭稳定形成后,其内部视为层流运动;
(3)鉴于平流铸造中带材冷却速率极大(约为105~106K/s),凝固时间极短,忽略非晶合金凝固过程中释放的潜热;
(4)平流铸造中,在上部液态金属的静压力及冲击力作用下,可认为薄带与结晶器表面紧密接触,即忽略熔潭/结晶器表面热阻的存在.
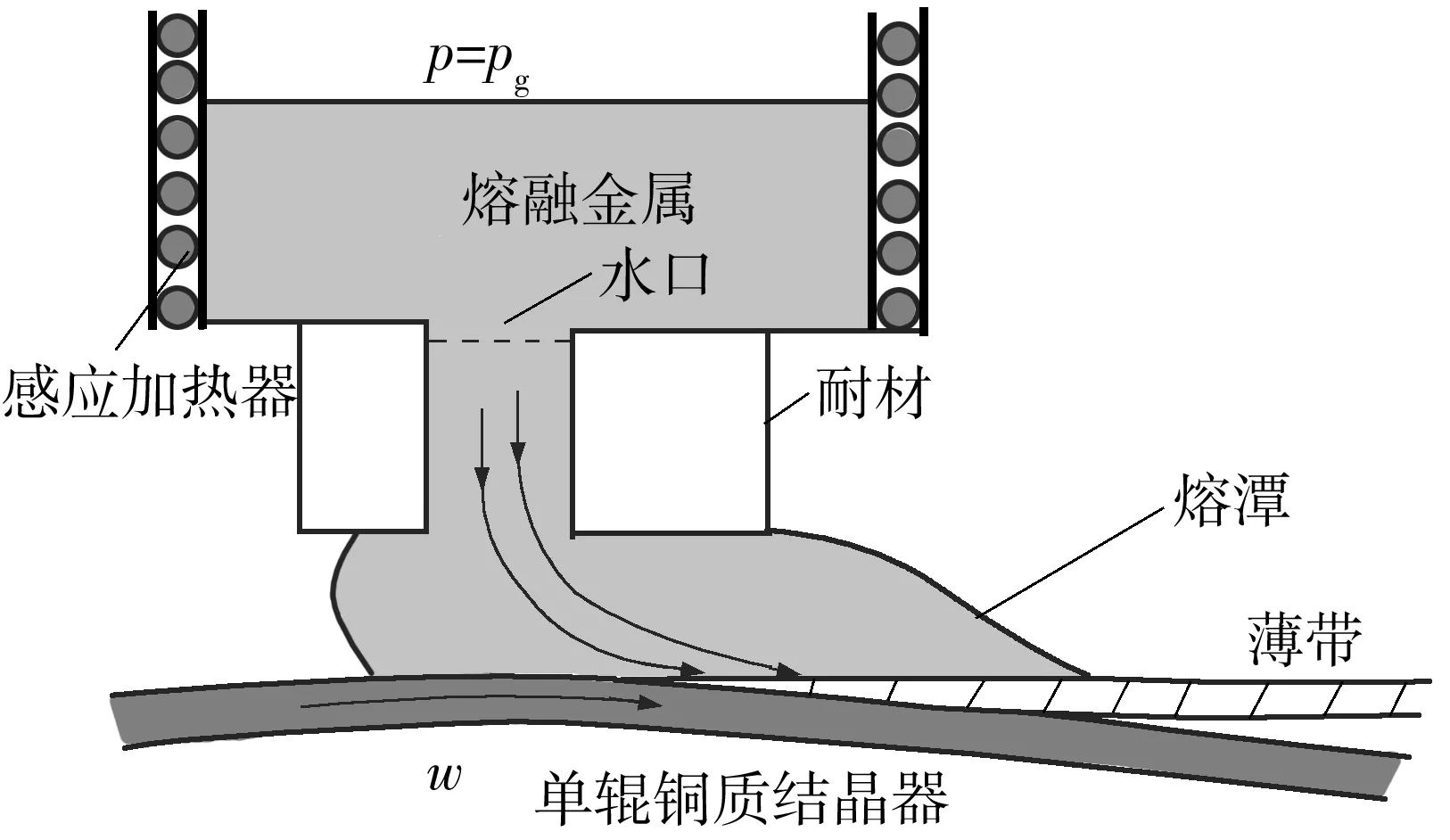
图1 平流铸造工艺示意图
1.2 模型描述
基于以上假设,数学模型采用基于笛卡尔坐标系的连续性方程(式(1))、动量方程(式(2))、传热方程(式(3))及VOF模型(式(4)和(5))来对熔潭形成过程及熔潭内部的流动传热现象进行描述.具体如下:
(1)
(2)
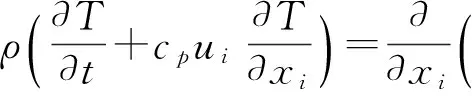
(3)
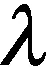
VOF模型中,各相流体的体积分数φq在计算域内是连续分布的,且在模型的每个控制单元中q相流体遵循以下法则:
(4)
此外,模型中各相的热物性参数M由各个控制单元内的所有相共同决定,并遵循以下关系式:
(5)
1.3 计算工况及热物性参数
表1给出了平流铸造过程中单辊结晶器的结构及工艺参数.表2和3分别列出了非晶合金、空气以及单辊结晶器用铍铜的热物性参数.所用非晶合金的化学式为Fe78Si9B13.对于非晶合金,当合金温度大于其玻璃化温度Tg(723 K)时,合金黏度由式(6)[15]计算;当合金温度小于Tg时,其黏度为1 Pa·s,以模拟凝固现象[6].此外,为考虑熔潭内熔体的对流换热效果及其上、下弯月面的辐射换热对熔潭内部温度场的影响,模型中液态金属的导热系数设为固态下的2倍,且将空气的导热系数放大2倍.
μ=0.1×exp[-3.652 8+734.1/(T-674)]
(6)
表1 平流铸造过程中单辊结晶器的结构及工艺参数
Table 1 Structural and technical parameters of single-roller mould during planar flow casting

参数参数值或设置结晶器转速/(m·s-1)22.6结晶器转动方向顺时针辊嘴间距/m0.0003喷嘴宽度/m0.00036结晶器外径/m1.164结晶器有效厚度/m0.022结晶器宽度/m0.1466带材厚度/m0.000028带材宽度/m0.106内槽个数150内槽宽度/m0.01水口入口速度/(m·s-1)1.7结晶器初始温度/K300浇铸温度/K1623.15
表2 非晶合金和空气的热物性参数
Table 2 Thermo-physical parameters of amorphous alloy and air
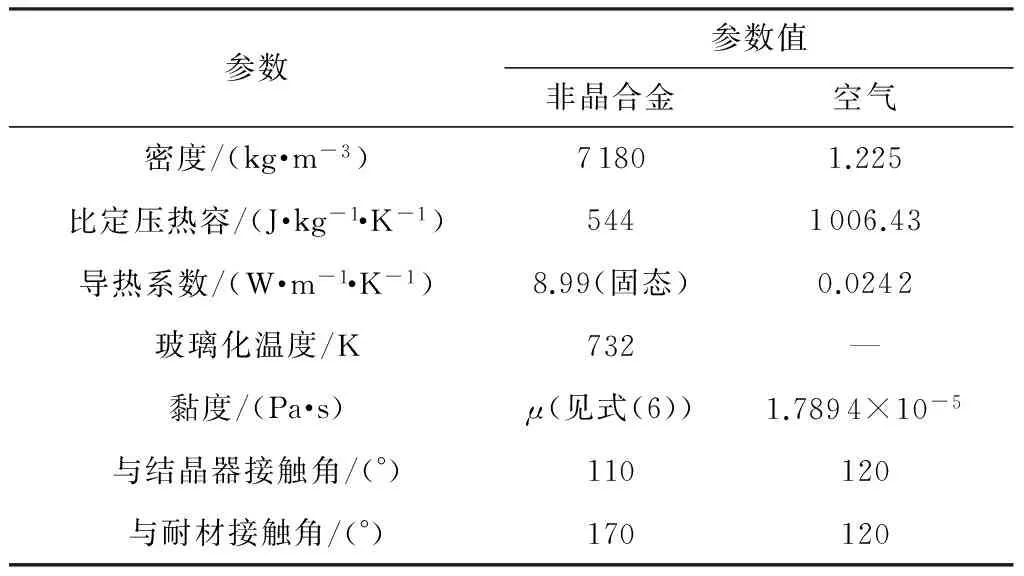
参数参数值非晶合金空气密度/(kg·m-3)71801.225比定压热容/(J·kg-1·K-1)5441006.43导热系数/(W·m-1·K-1)8.99(固态)0.0242玻璃化温度/K732—黏度/(Pa·s)μ(见式(6))1.7894×10-5与结晶器接触角/(°)110120与耐材接触角/(°)170120
表3 单辊结晶器用铍铜的热物性参数
Table 3 Thermo-physical parameters of Be-Cu used in single-roller mould

温度/K密度/(kg·m-3)比定压热容/(J·kg-1·K-1)导热系数/(W·m-1·K-1)线热膨胀系数/K-1293.1587504192401.76×10-5373.1587504192801.76×10-5473.1587504193161.76×10-5573.1587504193481.76×10-5673.158750419372—773.158750419385—
1.4 边界条件
图2给出了二维非稳态传热-多相流耦合模型的计算域及网格划分情况.其中,为精确描述熔潭以及带材的形成过程,对该区域内周向的网格间距进行了加密处理.对于结晶器区域,仅对结晶器沿周向的表层网格进行了加密处理,以在准确描述喷射熔体对结晶器的热冲击现象的同时,提高计算效率.为准确描述平流铸造过程中熔潭内的传热及相比行为,不引入界面理论换热系数[14],依据实际生产情况来建立数学模型.图3给出了该二维非稳态-多相流耦合模型的边界条件.其中:(1)AB和EF线表示空气入口,FG线表示空气出口,其速度初始时均为0 m/s,温度均为300 K(26.85 ℃);(2)BC和DE线表示喷嘴耐火材料,设为绝热条件以模拟预热效果;(3)CD线表示水口入口,其速度由质量守恒定律可得,浇注温度为1 623.15 K(1 350 ℃);(4)LM线表示熔潭区与结晶器区域的交界面,设为理想热接触状态;(5)AL线表示空气与结晶器的交界面,设为绝热条件;(6)MG线为带材与结晶器的交界面,综合换热系数为20 W/(m2·K)[14];(7)滑移边界条件,速度等于结晶器转动线速度;(8)HI线表示单辊结晶器内部冷却界面,冷却水温度为300 K[14],综合换热系数为22 988 W/(m2·K).

图2 二维非稳态-多相流耦合模型的计算域及网格划分
Fig.2 Computational domain and grid generation of 2D unsteady-multiphase flow coupled model
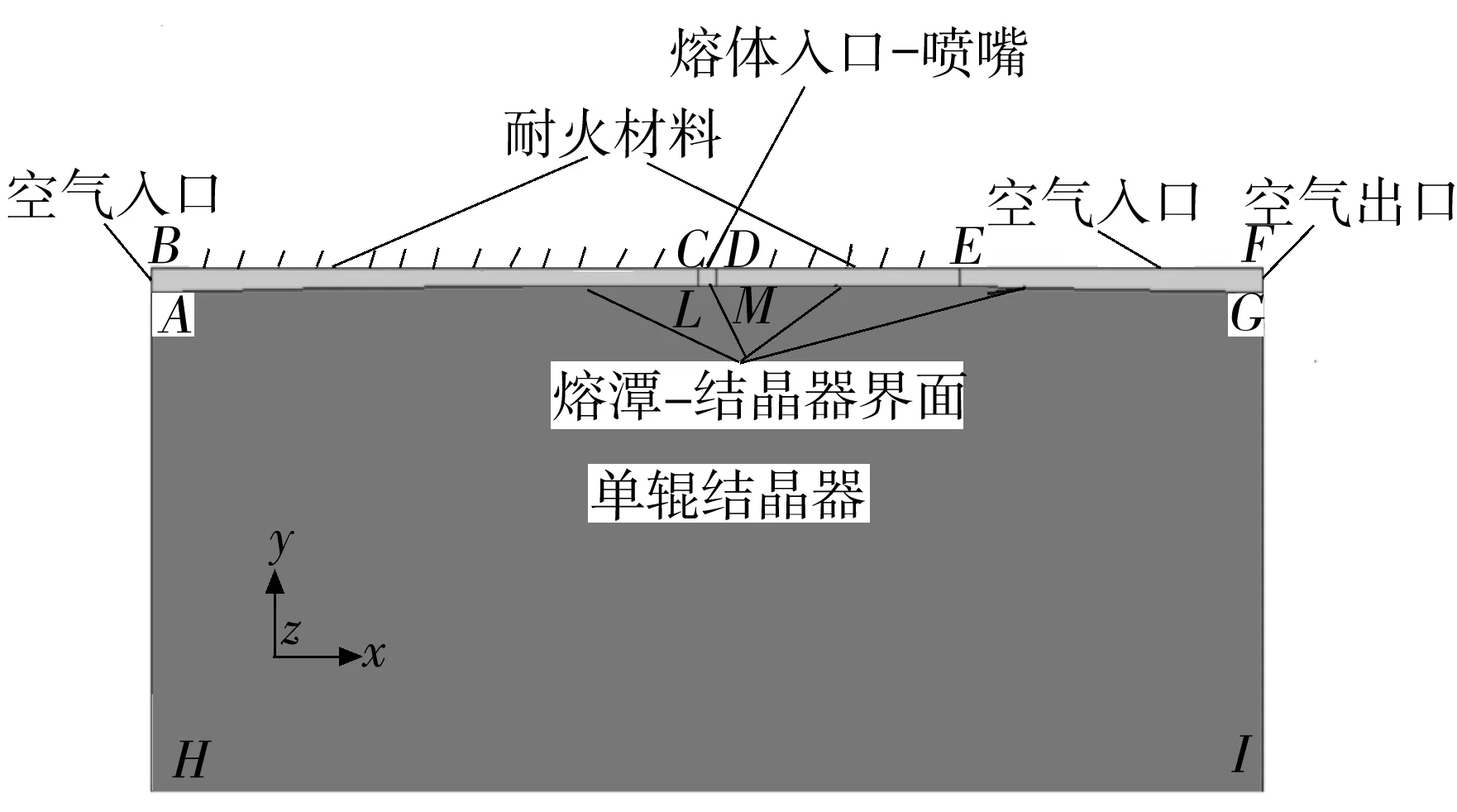
图3 二维非稳态-多相流耦合模型的边界条件示意
Fig.3 Schematic diagram of boundary condition of 2D unsteady-multiphase flow coupled model
由表1可知,单辊结晶器周向上均匀分布着150个东西向贯通的水槽.基于对称性原则,图4给出了单辊结晶器传热模型的计算域及网格划分情况.该模型的边界条件如下:结晶器外表面的热边界条件由前述二维非稳态传热-多相流熔潭模型获得;结晶器内与中轴接触面的综合换热系数为10 000 W/(m2·K),水槽各内面采用第3类热边界条件,且换热系数hw(见式(7))由努赛尔赫数确定.此外,为模拟结晶器铜辊的旋转运动过程,采用添加子程序方式(UDF)将上述边界条件处理为随时间变化的热边界条件.
(7)
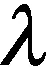
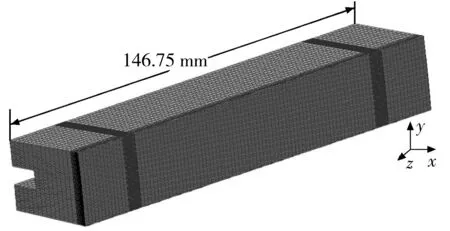
图4 3D非稳态传热模型的计算域及网格划分
Fig.4 Computational domain and grid generation of 3D unsteady heat transfer model
2 结果与讨论
2.1 熔潭形成过程中的流动与传热行为
图5示出了平流铸造过程中不同时刻t下熔潭形状的变化.熔体离开喷嘴时,在表面张力的作用下,熔潭中部的熔体向上收缩,形成如图5(a)所示的W形;熔体内惯性力大于表面张力时,如图5(b)所示,形成了一个V形的液滴状;约在0.150 ms时,该液滴与结晶器铜辊表面接触,如图5(c)所示;进一步地,在铜辊的旋转运动作用下,约在0.325 ms时形成了熔潭的上、下弯月面雏形,如图5(d)所示;约在1.000 ms时,如图5(e)所示,熔潭的上弯月面形状已基本稳定成C形,但因入口速度较大(1.7 m/s),下弯月面在喷嘴右侧形成一个垂直的熔体通道,而在结晶器高速旋转运动(22.6 m/s)下,该垂直段长度不断减小(约在0.350~2.000 ms时间范围内),并约在2.200 ms时消失(如图5(f)所示);此外,对比图5(f)、5(g)和5(h)可知,约从3.200 ms时起,熔潭形状基本稳定不变,其中上弯月面呈C形,下弯月面呈带波纹的斜坡状.

图5 不同浇铸时刻熔潭形状的变化
图6给出了熔潭形成过程中其内熔体的瞬态流动及传热行为,其中的黑粗虚线和白粗虚线代表熔潭与空气的交界面.如图6(a)所示,熔体未与结晶器铜辊表面接触时,在熔潭上弯月面抑制作用下,部分空气在熔潭上游形成沿逆时针方向的回流,另一部分空气则通过熔潭底部与结晶器铜辊表面之间的间隙后加速流向熔潭下游.在该空气对流换热作用下,熔潭附近空气被迅速加热,平均温度约由300 K(26.85 ℃)升至900 K(626.85 ℃).当熔体与结晶器铜辊表面接触并形成了上、下弯月面雏形时,如图6(b)所示,在结晶器的旋转及熔潭的分隔作用下,空气在熔潭的上、下游均形成了逆时针方向的回流.在这些回流的对流换热作用下,熔潭附近被加热的空气区域有所增大.此外,在该时刻,经喷嘴垂直进入熔潭的熔体到达结晶器铜辊表面后,在粘性力的作用下,其方向转为沿铜辊表面的切线方向.当熔潭形状稳定时,如图6(c)可知,与图6(b)相比,熔潭的上、下游空气回流区域以及被加热区域得到了充分的发展.值得一提的是,由于熔潭的下弯月面与喷嘴耐材面之间的区域较小,该区域内空气回流速度较小,仅约0.2 m/s,即有死区的存在,进而导致该区域内的空气温度与熔体温度相当,对熔体起到了一定的保温作用.此外,从图6(c)还可知,熔潭形状稳定后,熔体在上弯月面附近形成了一个顺时针方向的回流,有利于熔潭内熔体的过热耗散.靠近熔潭下弯月面的熔体则沿结晶器周向流动,且其流线与下弯月面形状相似.
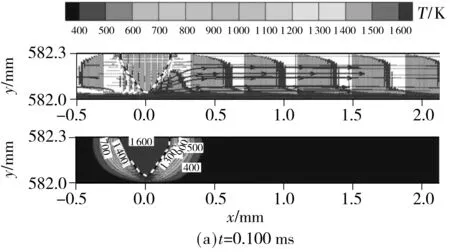

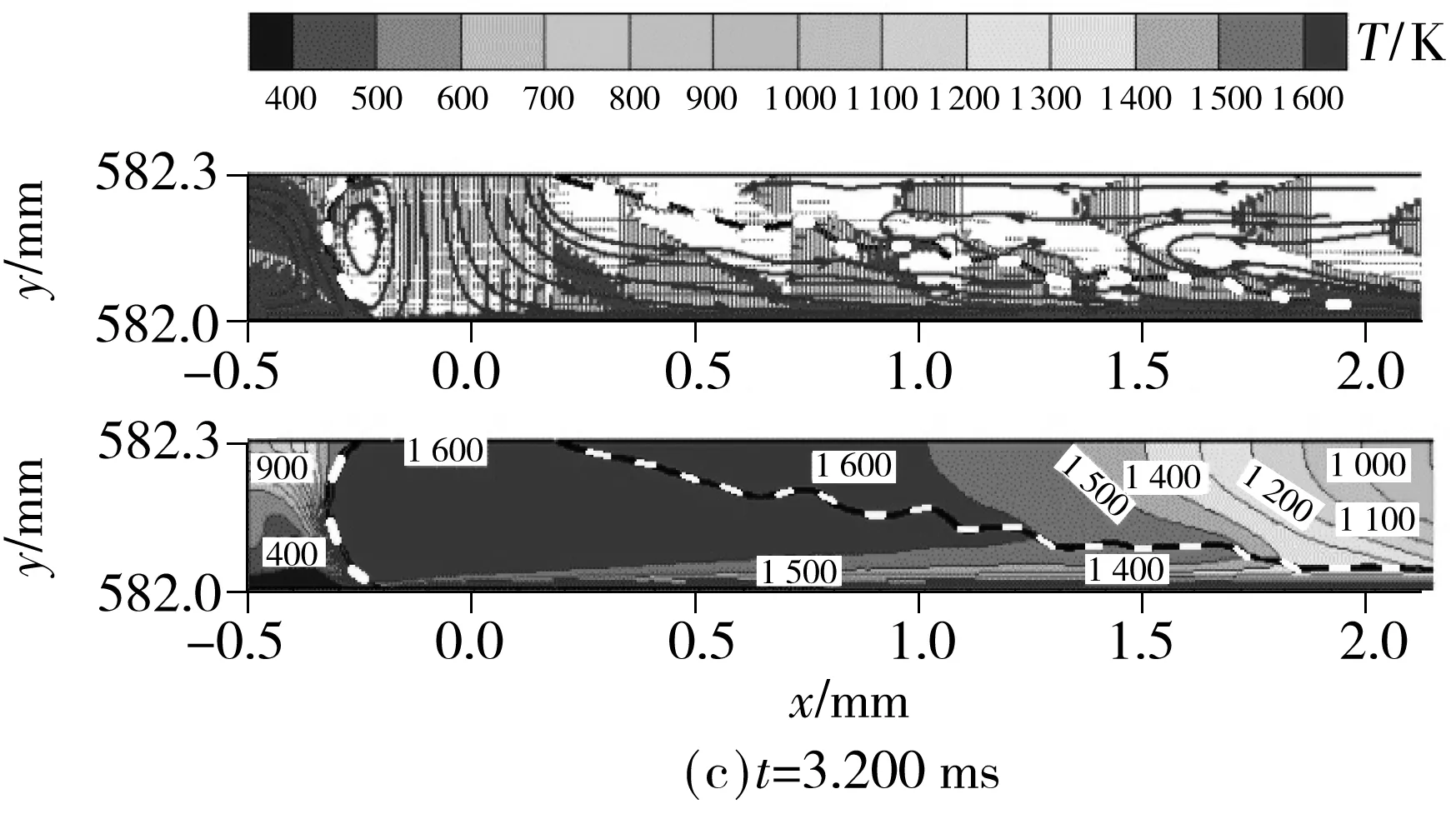
图6 熔潭形成过程中其内熔体的瞬态流动及传热行为
Fig.6 Transient melt flow pattern and heat transfer behavior during the formation of puddle
2.2 单辊结晶器传热模型边界条件的确定
为定量描述平流铸造过程中单辊结晶器的热状态,以分析和判断结晶器的膨胀变形行为,进而制定和优化相应生产工艺,在熔潭区模型的基础上,结合生产数据,对单辊结晶器的传热边界条件进行研究.
2.2.1 熔潭区
图7给出了熔潭区范围(以玻璃化温度作为凝固终点)内的热流密度分布情况.由图7(a)可知,当前工艺条件下,熔潭区的总长度为5.3 mm.熔潭区域内的热流密度在结晶器旋转方向呈先增加后减小的趋势.若选用图7(b)所示的热流密度曲线作为熔潭区热边界条件,需对当地网格进行进一步细化,不利于计算效率的提高.为此,如图7(b)所示,模型中将熔潭区划分为3个区域,采用平均热流作为边界条件,以便在保证计算精度的同时提高计算效率.各区长度分别为0.8、1.2和3.3 mm,相应的平均热流密度分别为779、278、40 MW/m2.

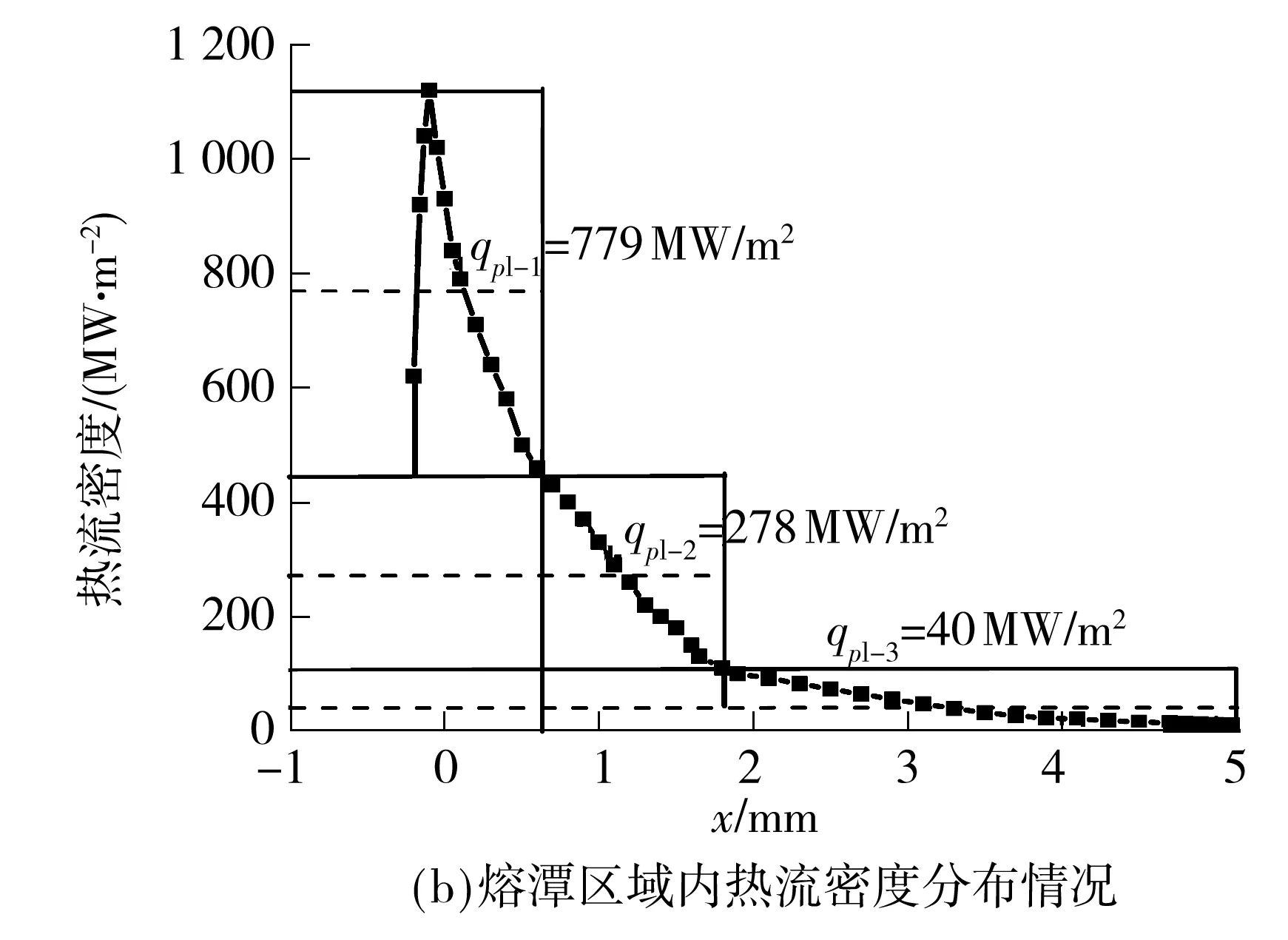
图7 熔潭区域范围及区域内热流密度分布情况
Fig.7 Illustration of puddle zone and heat flux distribution in the puddle zone
2.2.2 带材覆盖区
生产过程中,带材在熔潭成形后将包裹在结晶器表面并随之顺时针转动,当转动至约75°(文中试验采用)或270°左右时,由卷取机将带材卷取成材以保温.定义水口喷射处为结晶器的0°位置,为此,需对带材覆盖区的热边界条件进行研究.
图8给出了熔潭区域终点处的温度分布情况.结合图7(a)可知,带材成形后,其热面和冷面(靠近结晶器表面)的温度分别为723和448.98 K.考虑到带材厚度(0.028 mm)较小,模型中以带材成形后其温度在厚度方向呈线性分布这一特征作为初始条件,以带材热面为空冷条件(换热系数为50 W/(m2·K))作为热边界条件,以实测卷取带材温度作为定解条件,进行了大量的试错计算试验.结果表明,当带材冷面热边界条件为-4.8×105W/m2时,带材旋转至75°处的温度约为429.15 K(156 ℃),与实测值基本相符.为此,带材覆盖区范围内结晶器表面的热边界条件(热流密度)可选择为4.8×105W/m2.

图8 熔潭区域终点处的温度分布
2.2.3 空冷区
空冷区的边界条件采用第3类热边界条件(对流换热),且考虑到结晶器的高速转动效果,换热系数设定为50 W/(m2·K),环境温度为300 K.
2.3 单辊结晶器热状态研究
基于3D非稳态结晶器传热模型及2.2节中所述的传热边界条件,图9给出了结晶器270°位置处的表面温度分布及中心(距结晶器侧面0.073 3 m)温度随时间变化的模拟值与实测值,其中实测值采用热像仪获得.由图9可知,与实测值相比,模拟得到的结晶器270°位置处的表面温度沿轴线的分布情况基本一致,且其最大相对误差均仅在±4 ℃范围内.对于结晶器270°位置处的表面中心温度,其模拟值与实测值随时间变化的趋势也基本一致.此外,由该表面中心温度变化历程可知,模型所计算的结晶器热状态平衡时间与实测的相同,均为20 s,且结晶器达到热平衡后,其温度最大相对误差值均仅在±1 ℃范围内.综上可知,该模型所计算的温度场能真实反映结晶器的热状态变化.
图10为结晶器达到热状态平衡后,其周向不同位置的径向横截面上中心处温度沿径向的分布.结晶器表面任一轴向中心位置转至高温熔体冲击点时,其温度急剧升高,最高可达513.5 K(240.35 ℃),且在距表面0.000 4 m范围内形成了一个热冲击区.之后,在结晶器冷却效果下,该表面的中心温度在顺时针旋转运动过程中不断下降,其中,旋转至靠近熔潭区(结晶器的345°处)时,结晶器表面中心温度约为337.85 K(64.7 ℃).
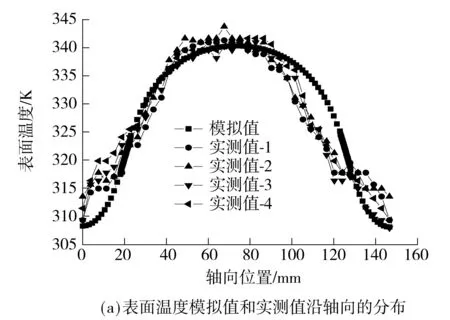
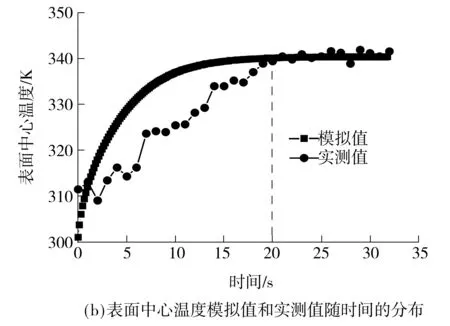
图9 单辊结晶器270°位置处的表面温度分布及中心温度随时间变化的实测值与模拟值的对比
Fig.9 Comparison between the measured and the simulated results of temperature distribution and center temperaturevarying with time at the location of 270°of single-roller mould
结合上述结晶器的热状态结果,表4列出了结晶器径向热膨胀估算值(由式(7)得到)、周向热膨胀对径向热膨胀的贡献估算值(由式(8)得到)及实测热膨胀平均值的对比.其中,结晶器表面中心平均温度由图10(b)获得,约为343.85 K(70.7 ℃);结晶器表面中心热膨胀测量位置位于结晶器的120°位置处.由表4可知,与结晶器径向热膨胀相比,周向热膨胀对生产过程中结晶器的实测总膨胀量的贡献较大,贡献率约为96%.然而,与结晶器实测膨胀量相比,周向热膨胀对径向热膨胀的贡献估算值较大.形成该现象的原因可能是:(1)结晶器采用过盈配合方法装配,其内部存在较大的装配应力[8,10];(2)在结晶器内外面温度梯度作用(如图10所示)下,结晶器内部会对结晶器表面产生一定的压应力.
LR=∫0.5600.582αT(f(T)-Tm)dL
(8)

(9)
式中,LR为径向温差梯度引起的径向应变量,m;αT为铍铜的线性热膨胀系数,K-1;f(T)为结晶器表面中心温度沿径向的分布函数;Tm为结晶器初始温度,为300 K;LC为周向热膨胀量,m;ER为结晶器周向膨胀对径向的贡献量,m;Tm-a为结晶器表面平均温度,K;D为结晶器外径,m.

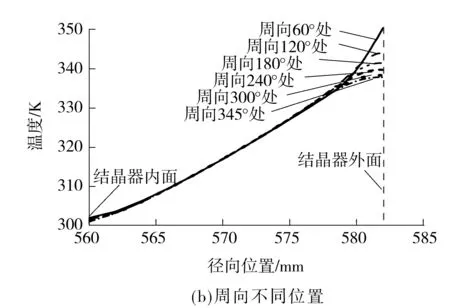
图10 结晶器热平衡后其周向不同位置处径向横截面上中心处温度沿径向的分布
Fig.10 Distribution of surface center temperature in radial direction at different radian positions of mould in the thermal equilibrium state
表4 结晶器热膨胀估算及实测结果
Table 4 Estimated and measured results of thermal expansion of mould

参数参数值径向热膨胀估算值/μm16.65~18.00周向膨胀对径向膨胀的贡献估算值/μm465.55实测热膨胀值样本数40实测热膨胀值范围/μm372~446实测平均热膨胀值/μm408
3 结论
文中在建立考虑液面形状变化和结晶器高速旋转行为的二维非稳态传热-多相流耦合模型及三维非稳态单辊结晶器传热模型的基础上,结合生产过程数据,对熔潭形成过程及单辊结晶器内的热状态进行了分析和研究,得到如下主要结论:
(1)在文中工艺条件下,熔潭稳定形成后,其上游和下游弯月面分别呈C形和带波纹的斜坡状;
(2)熔潭形状稳定后,经喷嘴进入熔潭的部分熔体在上弯月面附近形成了一个方向为顺时针的回流,利于熔潭内熔体的过热耗散,其他部分熔体则随结晶器顺时针周向流动,且其流线与下弯月面形状相似;
(3)非稳态单辊结晶器三维传热模型所预测的结晶器顺时针方向270°位置处的温度值与实测值的变化趋势基本一致,且热平衡后,最大相对误差仅在±4 ℃以内,此外,模型预测的结晶器热平衡时间与实测值基本相同,均为20 s,由此可知,该三维传热模型能真实反映结晶器内部的热状态;
(4)结晶器达到热平衡后,在高温熔体的冲击下,其表面中心温度最高可达513.5 K(240.35 ℃),且在距表面0.000 4 m(400 μm)范围内形成了一个热冲击区;
(5)由结晶器内部的热状态可知,与径向热膨胀相比,由结晶器周向热膨胀引起的径向热膨胀对结晶器总膨胀量的贡献较大,贡献率约为96%.
[1] Srinivas M,Majumdar B,Phanikumar G,et al.Effect of planar flow melt spinning parameters on ribbon formation in soft magnetic Fe68.5Si18.5B9Nb3Cu1alloy [J].Metall Trans B,2011,42(2):370- 379.
[2] Nagashio K,Kuribayashi K.Experimental verification of ribbon formation process in chill-block melt spinning [J].Acta Material,2006,54(9):2353- 2360.
[3] Yu H.A fluid mechanics model of the planar flow melt spinning process under low Reynolds number conditions [J].Metall Trans B,1987,18(3):557- 562.
[4] Hui X D,Yang Y S,Chen X M,et al.Transient heat transfer and fluid dynamics during the melt spinning process of Fe78Si9B12Mo amorphous alloy [J].Science and Technology of Advanced Materials,2001,2:265- 270.
[5] 惠希东,杨院生,陈晓明,等.单辊法制备非晶合金中的传热与熔体流动数值模拟 [J].金属学报,1999,35(11):1206- 1210. Hui Xi-dong,Yang Yuan-sheng,Chen Xiao-ming,et al.Numerical simulation of heat transfer and fluid flow during preparing amorphous alloy by single-roller spinning [J].Acta Metallurgica Sinica,1999,35(11):1206- 1210.
[6] Wang C B.Numerical modeling of free surface and rapid solidification for simulation and analysis of melt spinning [D].Iowa:Department of Mechanics Engineering,Iowa State University,2010.
[7] Chen C W,Hwang W S.A modified free surface treatment for the modeling of puddle formation in planar flow casting process [J].ISIJ Int,1995,35(5):393- 401.
[8] Theisen E A,Davis M J,Weinstein S J,et al.Transient behavior of the planar-flow melt spinning process [J].Chem Eng Sci,2010,65(10):3249- 3259.
[9] Liu H P,Chen W Z,Qiu S T,et al.Parametric investigation of interfacial heat transfer and behavior of the melt puddle in planar flow casting process by numerical simulation [J].ISIJ Int,2009,49(12):1859- 1901.
[10] Altieri A L,Steen P H.Substrate heating in the planar-flow melt spinning of metals [J].J Thermal Sci Eng Appl,2014,6(4):96- 104.
[11] Su Y G,Chen F,Chang C M,et al.Tuning the planar-flow melt-spinning process subject to operability conditions [J].Metall Trans B,2014,66(7):1277- 1286.
[12] Nobuaki Ito.Simulation model for solidification process in planar flow casting using the multi-zone method [J].ISIJ Int,2008,48(7):944- 953.
[13] Dhadwal R.Numerical simulation of a two-phase melt spinning model [J].Appl Math Model,2011,35(6):2959- 2971.
[14] Liu H P,Chen W Z,Qiu S T,et al.Numerical simulation of initial development of fluid flow and heat transfer in planar flow casting process [J].Metall Trans B,2009,40(7):411- 429.
[15] Yamasaki T,Shimada T,Ogino Y.Composition depen-dence of viscosity of Fe-B-Si liquid alloy [J].J Jpn Inst Met,1992,56(11):1229- 1234.
Numerical Simulation on Flow and Heat Transfer Behaviours During Planar Flow Casting of Amorphous Alloy Fe78Si9B13Ribbon
SunHai-bo1LiLie-jun1,2
(1.School of Mechanical and Automotive Engineering,South China University of Technology,Guangzhou 510640,Guangdong,China;2.Shaoguan-SCUT Institute of High-Tech Industries, Shaoguan 512000, Guangdong,China)
On the basis of two models, namely, the developed coupled model of two-dimensional transient heat transfer and multiphase flow and the model of three-dimensional transient heat transfer of single-roller crystallizers, the fluid flow and heat transfer behaviors during the puddle forming precess of the planar flow casting (PFC) of Fe78Si9B13as well as the heat transfer characteristics of rollers are investigated according to the production data. The results show that (1) under a given casting condition, the upstream and downstream meniscuses of the formed puddle are respectively in a crescent shape and in a slope shape with ripple; (2) the time for the crystallizer to reach a quasi-thermal equilibrium state is 20 s; (3) the impact of high temperature melts on the crystallizer causes an melt impact region of a depth of 0.000 4 m to form, where the maximum temperature in the center of crystallizer surface is about 513.5 K; and (4) in comparison with the radial thermal expansion, the circumferential thermal expansion of crystallizer plays a more important role in the actual total expansion, which accounts for 96%.
planar flow casting; amorphous alloy; flow; heat transfer; numerical simulation
2014- 12- 08
中国博士后科学基金资助项目(2014M562176) Foundation item: Supported by the China Postdoctoral Science Foundation(2014M562176)
孙海波(1986-),男,博士,助理研究员,主要从事现代先进铸造技术研究.E-mail: sunmyseven@126.com
1000- 565X(2015)11- 0067- 08
TF 777.1
10.3969/j.issn.1000-565X.2015.11.010

