航行器在空中飞行与水下潜航时的动力学特性*

杨海燕 林书玉 吝科

(1.陕西师范大学 物理学与信息技术学院， 陕西 西安 710061； 2.空军工程大学 空管领航学院， 陕西 西安 710051)

航行器在空中飞行与水下潜航时的动力学特性*

杨海燕1林书玉1吝科2

(1.陕西师范大学 物理学与信息技术学院， 陕西 西安 710061； 2.空军工程大学 空管领航学院， 陕西 西安 710051)

空气和水两种介质物理性质的巨大差异会对跨介质航行器的动力学环境产生复杂影响.文中以雷诺数为参考，采用CFX软件设计案例进行仿真，研究航行器在跨越不同流体介质时的动力学特性.仿真结果表明：跨越过程中流场存在一个雷诺数拐点，雷诺数小于拐点时，若水和空气的雷诺数相同，航行器的水、空流体动力学参数随攻角变化的趋势一致且数值相近；若水和空气的雷诺数相似，则存在一个匹配的飞行与潜航速度区间，仍能满足水、空介质间相似的动力学特性.文中研究结论可为航行器的航行控制提供设计依据.

雷诺数；数值仿真；气动特性；水动特性

水、空交替持续航行的航行器可弥补单介质航行器在多维态势感知、侦察、载运和攻击等方面的不足，属于空海一体作战的新概念航行器，统称为跨介质航行器，如美国国防部高级研究计划局(DARPA)提出的“潜水飞机”[1].然而，水、空两相介质物理性质的巨大差异，以及飞行器和潜航器设计思想的不同，都将增加跨介质航行器外形设计、动力配置和操纵控制的难度和复杂性.

文中针对空中飞行和水下潜航的动力学特性这一基础性问题展开研究，采用计算流体动力学方法，以雷诺数为参考，设计数值仿真案例，研究航行器在不同介质环境下的动力学特性，分析雷诺数对其流体动力学特性的影响，探索航行器适应不同介质环境的航行能力.

1 雷诺数相等环境的构建

跨水、空介质航行器的运动过程涉及空气和海水两种介质，不同介质环境对航行器的流体动力会产生不同影响[2- 3]，例如，流体密度对惯性类流体动力有直接的影响，在同样体积和速度条件下，水下潜航的惯性力要远大于空中飞行的作用力；粘性系数则是流体抵抗变形速率能力的量度，表现为沿航行器前进方向相反的作用力，两种流体的动力粘性系数大约相差两个数量级，在水下和空中也具有不同的表现.表1列出了理想条件下空气和水的物性参数.

表1 理想条件下空气和水的物性参数1)

Table 1 Physical parameters of air and water in ideal condition

介质ρ/(kg·m-3)v/(m·s-1)p/Paμ/(kg·s-1·m-1)空气1.2253401.0×1051.789×10-5水998.21500ρgh1.003×10-3

1)ρ—密度;v—速度;p—压力;μ—动力粘性系数.

雷诺数Re反映了流体微团所受的惯性力与粘性力之比，对流场特性有很大影响.它不仅提供了判断流体流动类型的标准，更实现了标度对称性，即边界状况或边界条件相似的两种流体，如果具有相同的雷诺数，则两种流体具有相同的动力学特征.因此，通过构建雷诺数相等的流体环境，对航行器飞行和潜航运动进行数值模拟和动力学特征分析，可为降低航行器在水空介质中的操控难度、提升航行能力提供设计依据.

理想条件下，空气和水的密度、粘性系数均为常值，航行器的特征长度l亦可认为不变，故可通过设计航行速度使航行器在相同的雷诺数环境下飞行和潜航.以15 ℃的空气和20 ℃的水为例，航行器在空气中的速度为va，在水下的速度为vw，则有

(1)

(2)

或

va=14.56vw

(3)

式中，下标a和w分别代表空气和水.

在上述公式所示的速度关系下，航行器在空气和水下的雷诺数大体相等.基于以上分析，文中在雷诺数相等条件下对航行器的空中和水下流场展开数值模拟，对比研究航行器飞行和潜航动力学特性.

2 网格模型和数值方法

2.1 网格模型

根据飞行和潜航的不同设计需求，水空两用航行器的外形设计需综合考虑水动性能和气动性能.为缓冲飞行器和潜航器的构型差异，融合构型相似的水下滑翔机和空投滑翔鱼雷的设计特点[4- 6]，并以“空中优化，水下可行”为原则，选择升力型构型作为文中的研究对象，物理模型如图1所示.

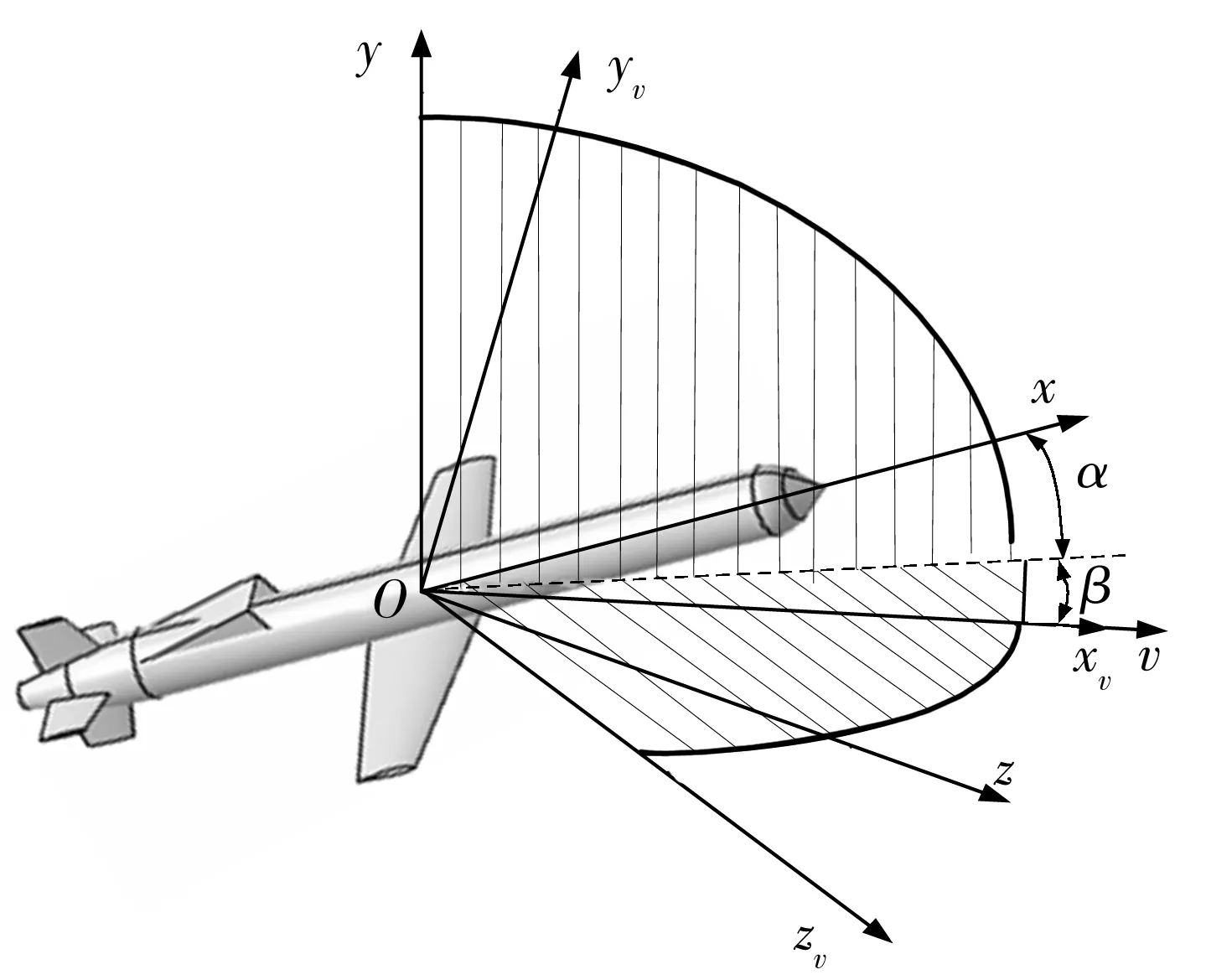
图1 升力型构型的物理模型

图1中，Oxyz为航行器坐标系，Oxvyvzv为速度坐标系，Oy轴与Oyv轴均在纵向对称面内.根据两坐标系之间的转换关系定义攻角α和侧滑角β——攻角α是航行器速度矢量(Oxv轴)在Oxy平面的投影与Ox轴的夹角，侧滑角β是航行器速度矢量与纵向对称面的夹角.

飞行和潜航的数值模拟可采用同一套网格模型[7].物理模型采用对称设计，模拟中无侧滑角，因此可应用对称边界条件，仅对一半流场进行数值模拟以节约计算资源.根据模型尺度及计算要求建立恰当的控制区域——长为10S、高为6S、宽为5S的长方体(S为航行器长度)，以保证仿真真实性和计算准确性.采用ICEM的Block划分网格，网格如图2所示.

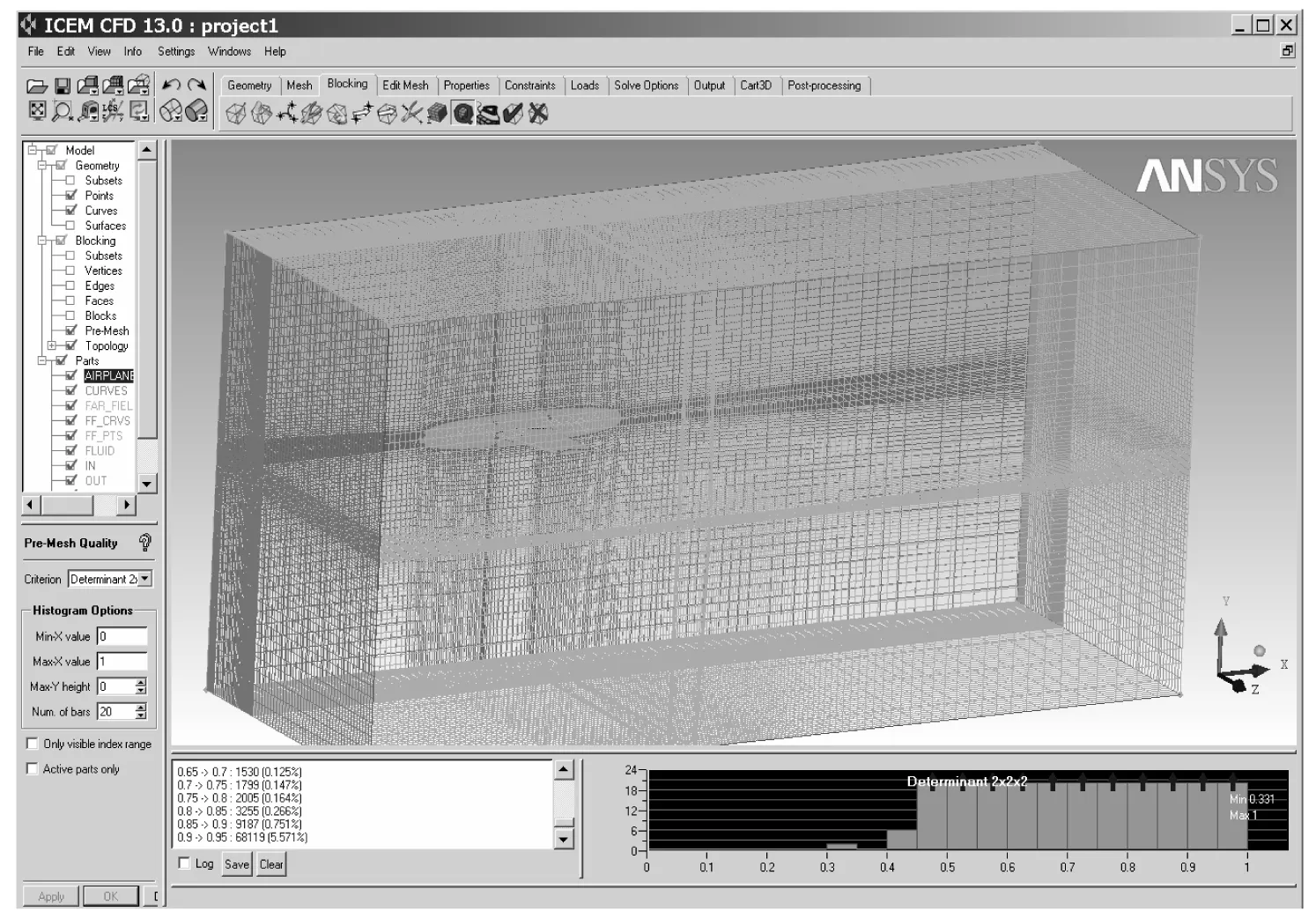
图2 网格模型

如图2所示的计算域全局网格，网格总数约126万，网格质量在0.30～0.35区间的仅2个，总体网格质量在0.50以上，符合计算要求.

2.2 模拟方法

航行器以0.5 m/s在水下潜航时，其雷诺数为1.6×106，已超过临界雷诺数，故仿真中需采用湍流模型.空中和水下不同的航行环境要求选择相应的湍流模型，根据通用标准模型和风洞、水洞实验数据对数值计算方法进行的准确性验证结果[8- 9]，分别选择剪应力输运(SST)湍流模型和雷诺应力(RSM)湍流模型作为空气流场和水流场仿真计算的湍流模型.

求解控制方程为三维雷诺平均守恒型纳维-斯托克斯(N-S)方程，计算区域采用有限体积法进行离散，采用SIMPLEC方法计算压力速度关联方程，时间项采用中心差分格式，对流扩散项采用二阶迎风格式，壁面附近采用自动壁面函数.

3 计算结果分析与讨论

文中主要对纵向流体动力学特性进行比较分析，包括：升力系数Cl，阻力系数Cd，升阻比K和俯仰力矩系数Cm.其定义为

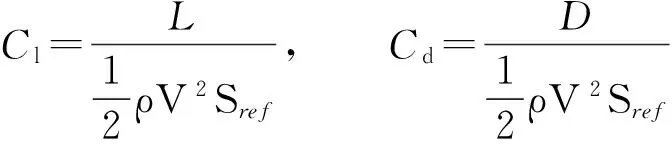
式中：L为升力，为突出对流体动力学特性的比较，水下采用去浮力之后的动升力进行比较和分析；D为阻力，包括粘性阻力和压差阻力；Mz为俯仰力矩；Sref为参考面积，选用机体最大横截面积；c为机翼的平均气动弦长.

3.1 基于雷诺数相等的流体动力学特性分析

水下有翼航行器的速度大都在6海里/h左右[4]，以此为参考设定水下潜航速度为3m/s，对应的雷诺数为1.1×107，设定空中飞行的对比速度为43.7m/s.在侧滑角β=0°时，通过仿真研究攻角α的变化对动力学特性的影响.

由图3所示飞行和潜航升力系数对比可见：当攻角在±12°范围内时，二者的升力线斜率基本一致，升力系数与攻角成线性增长关系；但当攻角值超出±12°范围时，空中升力系数出现拐点，即α<-12°时，空中升力系数随着攻角绝对值的增大而增大，α>12°时，空中升力系数随着攻角绝对值的增大而减小，从而导致与水下升力系数的差异扩大.

图3 水、空升力系数对比

由图4所示的飞行和潜航阻力系数对比可见：阻力系数曲线是开口向上的二次曲线，α=0°时出现极小值；水下和空中的阻力系数曲线形状和数值基本一致；随攻角绝对值增大，阻力系数差值逐渐增大，当α=±10°时，空中和水下阻力系数的绝对差为1.8×10-3，相对差达3.35%，但在±12°的攻角范围内，其相对差未超过6%.

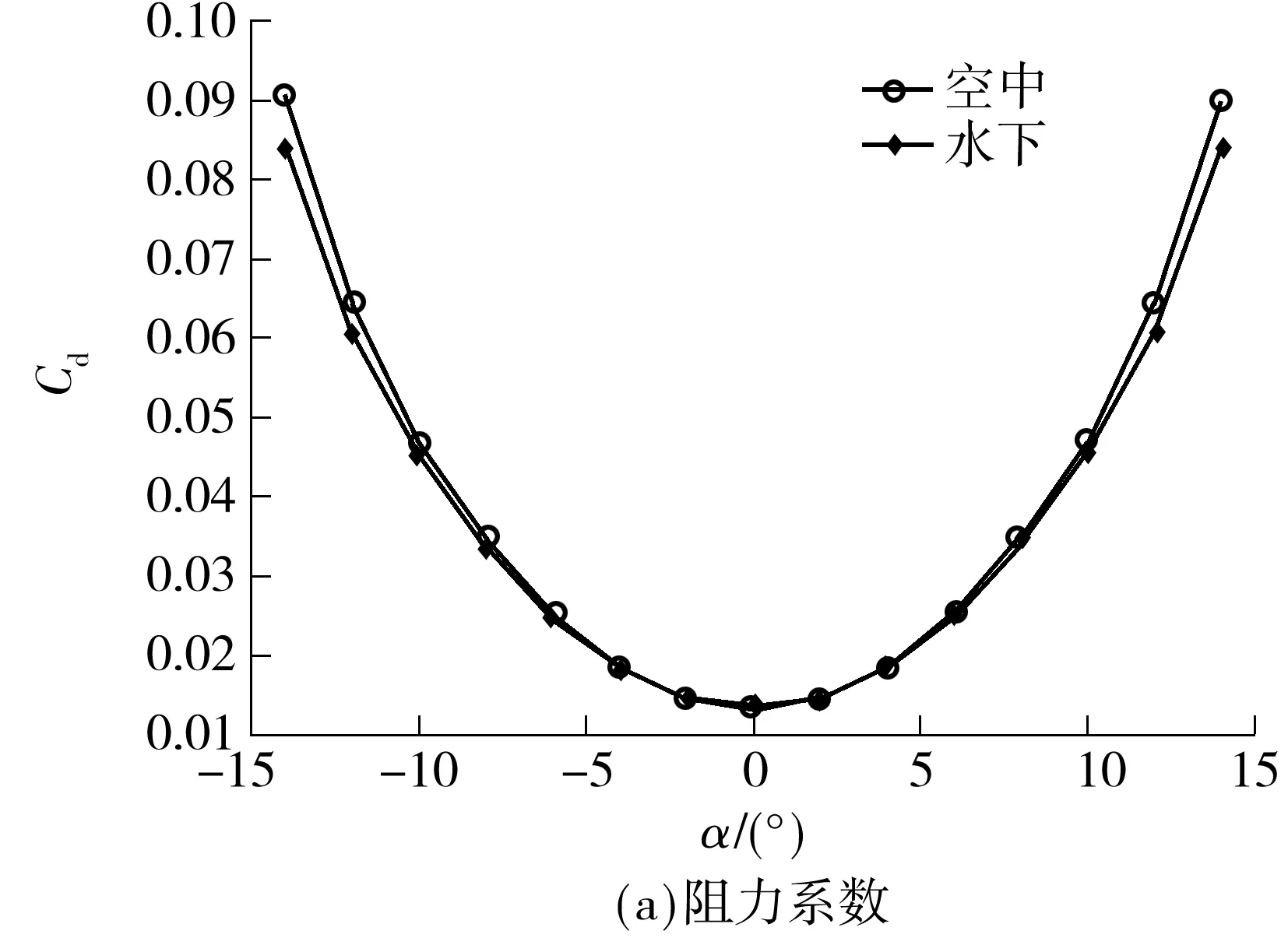
图4 水、空阻力系数对比

由图4可知，航行器飞行和潜航中升力和阻力特性基本相同，因此其升阻比特性也应当相似.如图5所示，在±5°的攻角范围内，水、空升阻比曲线随攻角的变化趋势一致，且数值几乎相等；随攻角绝对值增大，升阻比差值逐步增大，当α=±10°时，相对差达6.8%，当α=±12°时，相对差接近20%.

如图6所示，俯仰力矩系数的比较结果与升力系数相似.攻角在±10°范围内时，水、空俯仰力矩系数的斜率基本一致，数值几乎相等；攻角大于±10°范围时，俯仰力矩系数在空中和水下的差值逐渐增大；α=±12°时，相对差达7%.

以上仿真验证说明：航行器在雷诺数为1.1×107对应的飞行速度和潜航速度下航行时，若攻角在±10°范围内变化，空中和水下的动力学参数随攻角的变化趋势相同，并且在数值上比较相近；当攻角变化超出±10°范围时，空中和水下动力参数的变化趋势发生改变，数值差逐渐增大，尤其在攻角绝对值大于12°后，数值差急剧增大.

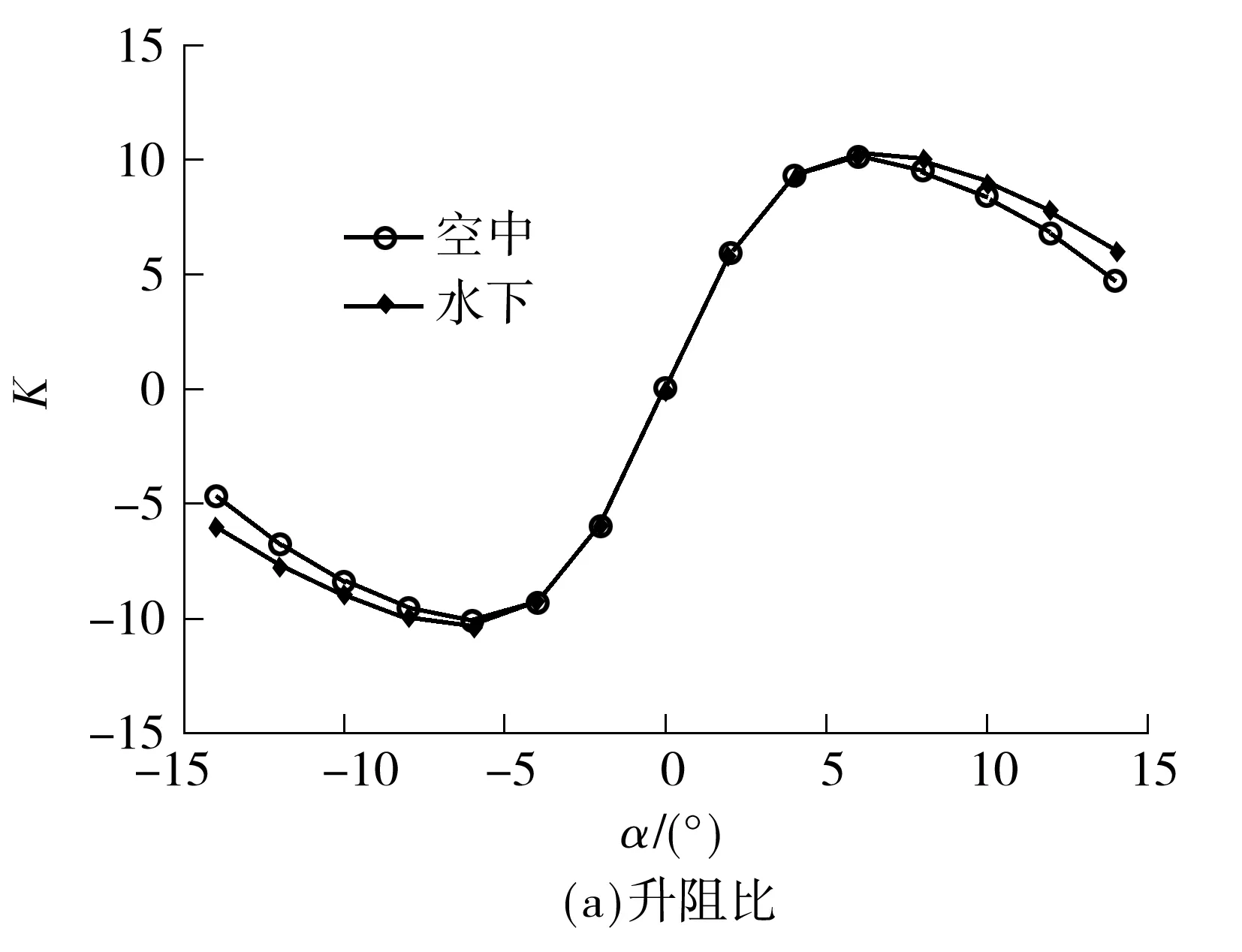
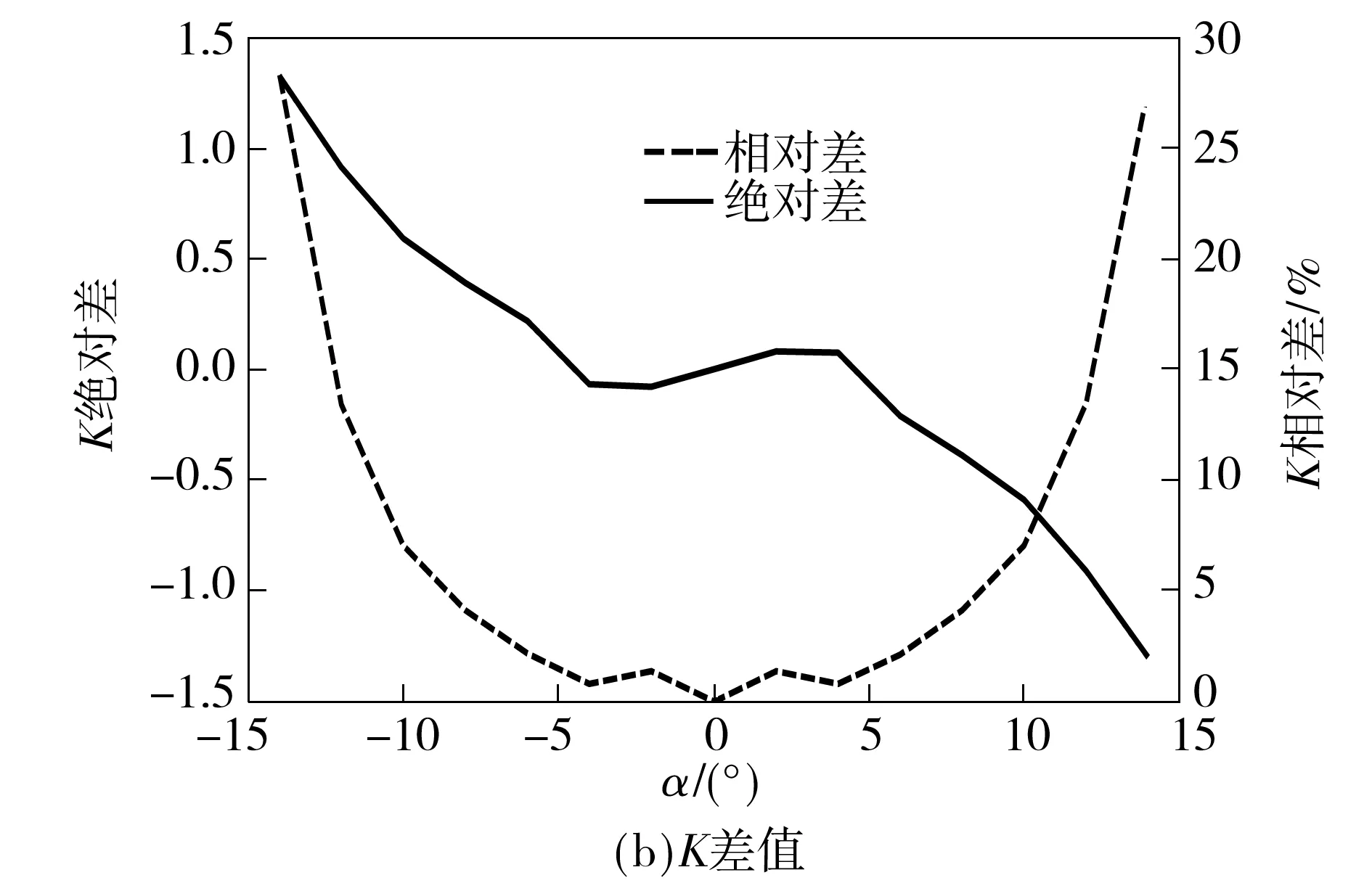
图5 水、空升阻比对比

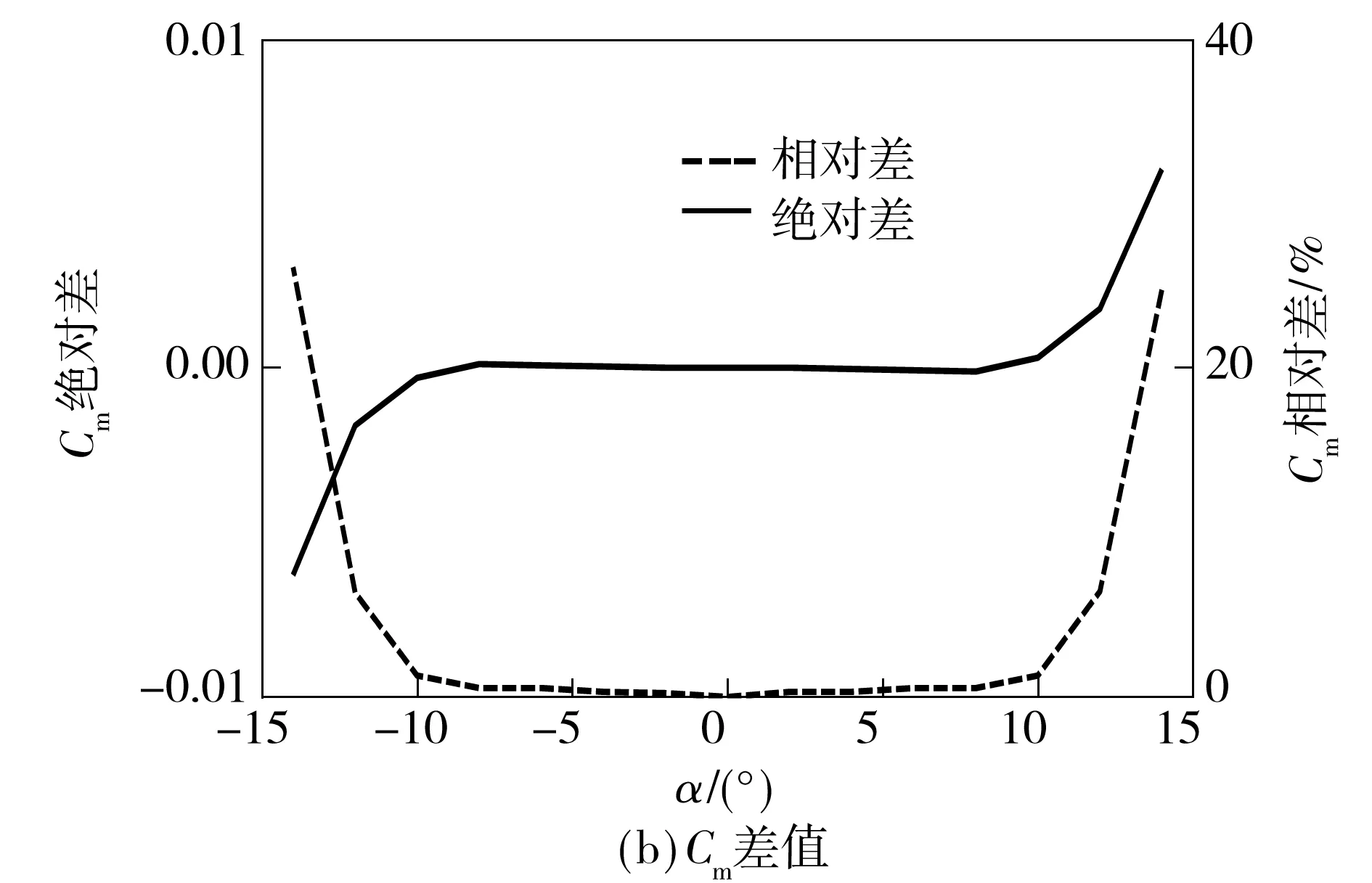
图6 水、空俯仰力矩系数对比

3.2 雷诺数对流体动力学参数的影响分析

雷诺数变化对航行器在空中和水下两相环境中各动力学参数的影响不同，欲进一步探析空中飞行与水下潜航的动力学关系，需在更大的雷诺数范围内进行研究.图7给出了雷诺数在0.6×107～5.5×107范围内、对应飞行速度为14～250 m/s、潜航速度为1～17 m/s时，航行器在两相介质中的动力学参数变化.

由图7可知：在所研究的雷诺数范围内，升力系数在空中和水下均随雷诺数增加而升高，其中在空中的升幅较大；俯仰力矩系数随雷诺数增加而降低，也是在空中的变化幅度较大；水、空阻力系数随雷诺数的变化趋势不同，其中水下阻力系数随雷诺数的增加一直缓慢下降，而空中阻力系数随雷诺数的增加先降低后升高，在雷诺数为2.7×107左右达最低点，这是由于速度提高使得航行器局部产生激波，造成阻力增大；升阻比由于阻力系数的巨大变化也呈现不同的作用规律.

根据阻力系数在两相介质中随雷诺数的不同变化趋势，确定雷诺数拐点为2.7×107.在Re<2.7×107时，空中和水下的动力学参数随雷诺数变化的趋势相同，数值接近；Re>2.7×107时，空中和水下的动力学参数随雷诺数变化的规律不同.因此，下文在雷诺数拐点之前讨论飞行和潜航的动力学特性关系.

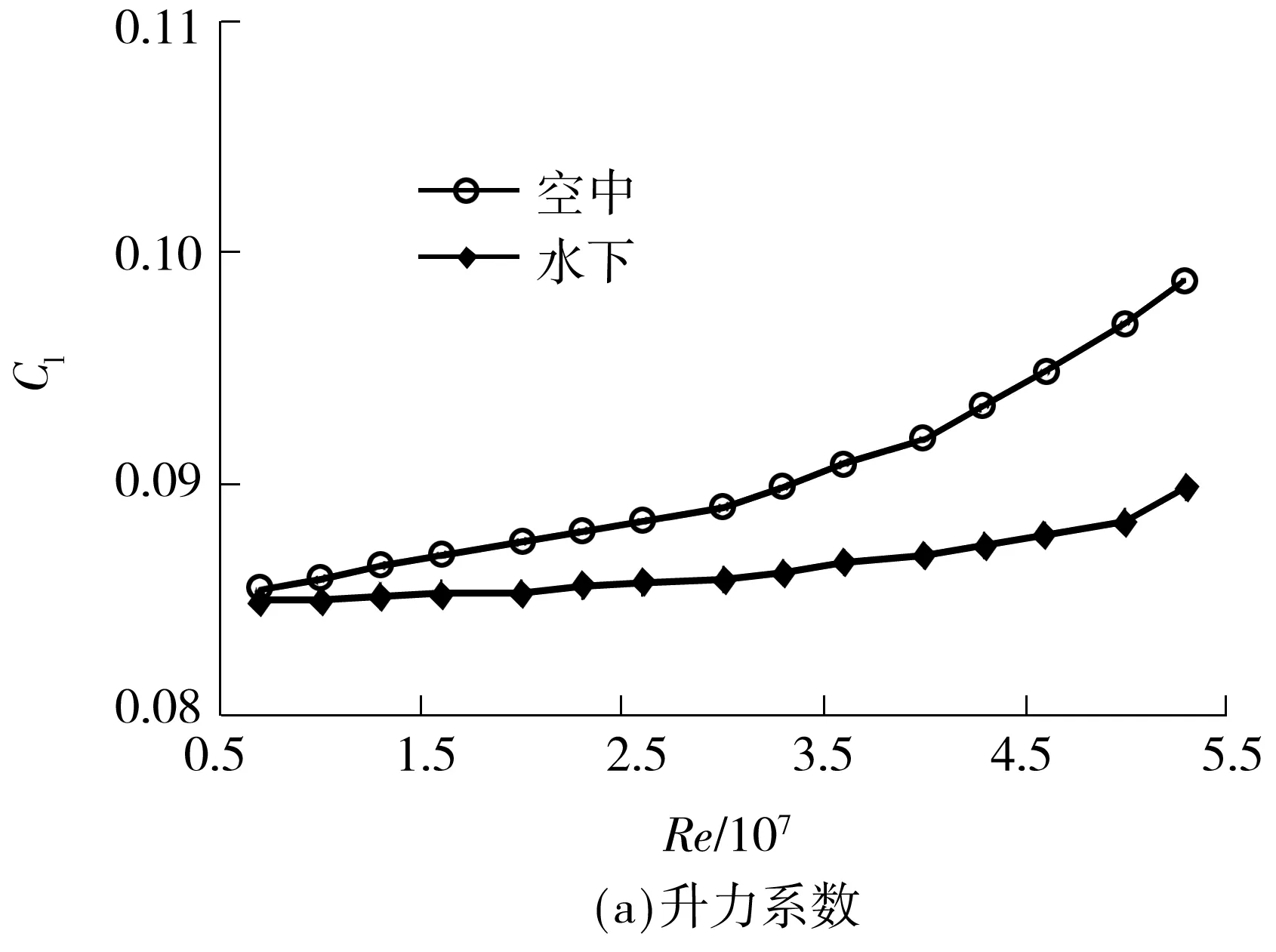
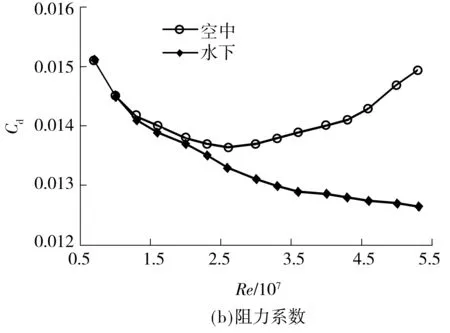
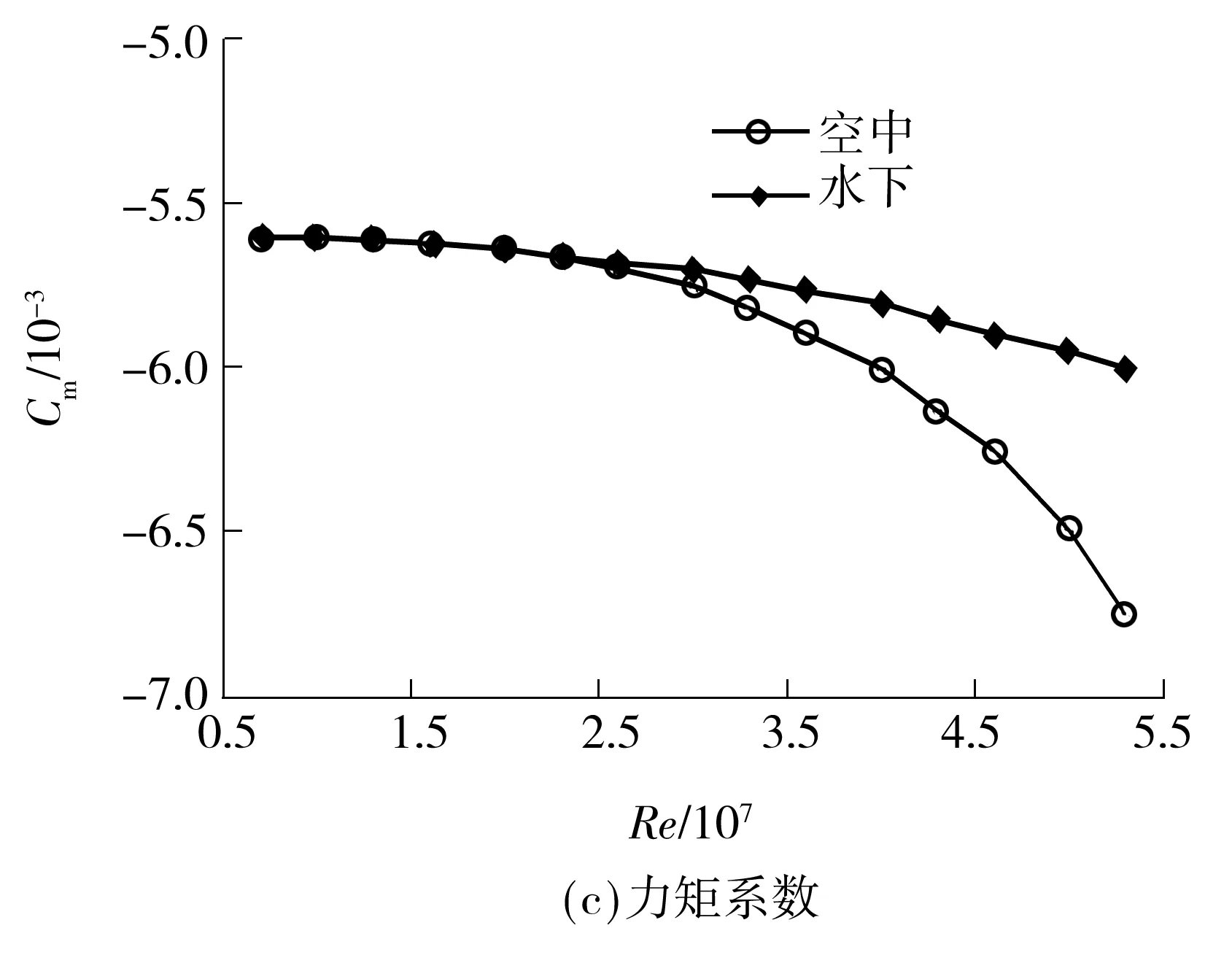
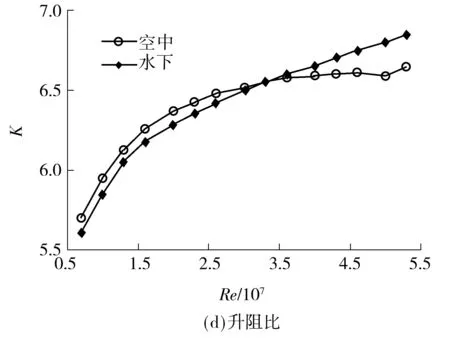
图7 雷诺数对水、空动力学参数的影响

Fig.7 Influence ofReon aerodynamic and hydrodynamic cha-racteristic parameters

3.3 基于雷诺数相似的流体动力学特性分析

在雷诺数拐点之前，依据“空中优化，水下可行”的原则，固定水中雷诺数取值，使空中雷诺数取值处于一个变化的范围，于是水中雷诺数与空中雷诺数区间有了一个映射关系，称为雷诺数相似.

在雷诺数相似情况下研究空中飞行和水下潜航的动力学特性关系，根据公式(1)，可以理解为将基于雷诺数相等的匹配速度拓展为基于雷诺数相似的匹配速度区间.固定水中雷诺数为2.7×107，空中雷诺数在此基础上逐渐减小，根据式(2)和(3)，水下潜航速度为9 m/s，飞行速度从131 m/s开始递减变化.相应的数值仿真结果如图8所示，并选择飞行速度117 m/s进行比较.

如图8所示，不同航行状态下，当攻角在±10°范围内变化时，航行器空中与水下的动力学参数随攻角变化的趋势相同，数值相近，尤其在±5°的攻角范围内，数值几乎相等；当攻角超出±10°范围后，航行器空中与水下的动力学参数随攻角的变化趋势相似，但数值相差很大，且随着飞行速度的降低，各动力学参数的差值减小.例如，当α=10°、飞行速度为131 m/s时，升力系数的相对差达8.2%，阻力系数的相对差达16.9%，俯仰力矩的相对差达5.8%，升阻比的相对差达21.4%；将飞行速度调整为117 m/s后，与水下潜航相应的上述4个动力学系数的相对差分别为2.8%、6.4%、2.4%和8.7%.

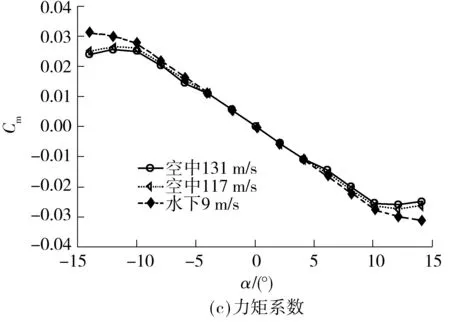
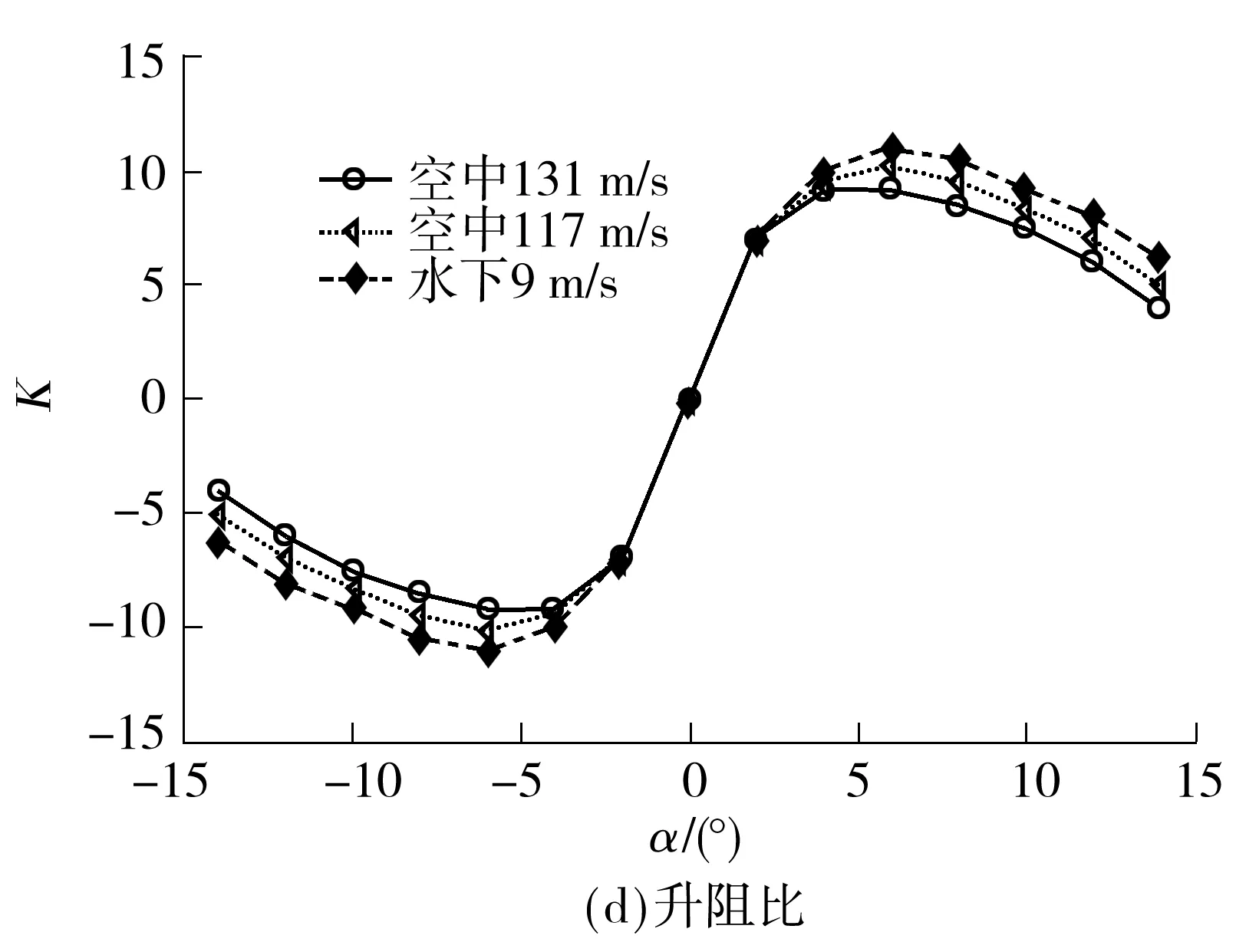
图8 不同航行状态下的水、空动力学参数比较

Fig.8 Comparison of aerodynamic and hydrodynamic characte-ristic parameters of water and air in different voyage conditions

保持水下潜航速度不变(9 m/s)，增大飞行速度递减变化范围，数值仿真结果显示：在攻角小于10°、飞行速度变化区间为106～121 m/s时，航行器空中与水下动力学参数的相对差均小于10%.因此可推断，在雷诺数相似的条件下，存在相应的飞行和潜航速度区间，以该速度航行时航行器的各动力学参数随攻角的变化趋势一致并且数值相近，即航行器获得相似的水空航行环境.

4 结语

文中在雷诺数相似的条件下为航行器搭建了水、空两相介质中的航行环境，通过数值模拟获得了航行器飞行和潜航的动力学关系，具体结果如下：

(1)航行器在跨越水、空介质的过程中，存在一个雷诺数拐点(Re=2.7×107)，在拐点之前，航行器在空中和水下的动力学参数随雷诺数变化的趋势相同，数值接近；在拐点之后，空中和水下动力学参数随雷诺数的变化规律不同.

(2)在雷诺数拐点之前，当攻角在±10°范围内时，航行器空中飞行和水下潜航的动力学参数受攻角变化影响的趋势相似且数值相近；当攻角超出±10°范围时，空中和水下动力学参数的变化趋势发生改变，数值差逐渐增大.

(3)在雷诺数拐点之前，依据“空中优化，水下可行”的原则，当水、空环境的雷诺数相似时，存在一个飞行速度区间与确定潜航速度之间的匹配映射，以该映射关系航行时，航行器在空中飞行的动力学特性与在水下潜航的相似.

在航行器的运动过程中，流体动力、力矩系数会直接影响控制系统的回路参数.当动力学参数相等或相近时，航行器在不同介质环境下对输入的动态响应特性相似，此时航行器在水、空介质中的操控将得到简化，航行能力得到提升.文中研究成果对航行器设计和弹道设计有指导意义.

[1] 陈建峰,杨龙塾.美国DARPA提出的“潜水飞机”概念 [J].现代舰船,2009(3A):38- 39. Chen Jian-feng,Yang Long-shu.American DARPA proposed the concept of submersible aircraft [J].Modern Ship,2009(3A):38- 39.

[2] 刘伟.潜水飞机总体设计与气动外形结构设计分析 [D].南昌:南昌航空大学飞行器工程学院,2012:21- 25.

[3] Hassan Ghassemi,Mahmoud Ghiasi.A combined method for the hydrodynamic characteristics of planting craft [J].Ocean Engineering,2008,35(10):310- 322.

[4] 赵宝强,王晓浩,姚宝恒,等.基于四元数的水下滑翔机建模与仿真 [J].计算机仿真,2014,31(7):355- 359. Zhao Bao-qiang,Wang Xiao-hao,Yao Bao-heng,et al.Underwater glider modeling and simulation based on quaternion [J].Computer Simulation,2014,31(7):355- 359.

[5] 张礴,宋保维,王司令.高空远程滑翔鱼雷弹道建模与仿真 [J].弹箭与制导学报,2012,32(2):142- 146. Zhang Bo,Song Baowei,Wang Siling.Modeling and tra-jectory simulation for high altitude long-range gliding torpedo [J].Journal of Projectiles,Rockets,Missiles and Guidance,2012,32(2):142- 146.

[6] 裴譞,张宇文,李闻白,等.跨介质飞行器气/水两相弹道仿真研究 [J].工程力学,2010,27(8):233- 240. Pei Xuan,Zhang Yu-wen,Li Wen-bai.Simulation and analysis on the gas/water two-phase ballistics of trans-media aircraft [J].Engineering Mechanics,2010,27(8):233- 240.

[7] 吝科,冯金富,张晓强,等.升力型潜水飞行器水空动力学特性研究 [J].舰船科学技术,2014,36(9):94- 97. Lin Ke,Feng Jin-fu,Zhang Xiao-qiang,et al.Research on the aerodynamic/hydrodynamic characteristic of lifting submersible aircraft [J].Ship Science and Technology,2014,36(9):94- 97.

[8] 张楠,沈泓萃,姚惠之.用雷诺应力模型预报不同雷诺数下的潜艇绕流 [J].船舶力学,2009,13(5):689- 696. Zhang Nan,Shen Hong-cui,Yao Hui-zhi.Prediction of flow around submarine at different Reynolds numbers with Reynolds stress model [J].Journal of Ship Mechanics,2009,13(5):689- 696.

[9] 达兴亚,周为群,赵忠良.窄条翼导弹模型摇滚运动动力学特性研究 [J].空气动力学学报,2014,32(2):154- 157. Da Xingya,Zhou Weiqun,Zhao Zhongliang,et al.Research on the kinetics of rock motion for a missile model with strake wings [J].Acta Aerodynamica Sinica,2014,32(2):154- 157.

Investigation into Aerodynamic and Hydrodynamic Characteristics of Trans-Media Vehicle

YangHai-yan1LinShu-yu1LinKe2

(1.College of Physics and Information Technology,Shaanxi Normal University,Xi’an 710061,Shaanxi,China;2.College of Air Traffic Control and Navigation,Air Force Engineering University,Xi’an 710051,Shaanxi,China)

The huge physical-characteristic differences between air and water would produce complicated impact on the dynamic environment of trans-media vehicles. In this paper, with the Reynolds number(Re) as reference, the dynamic property of the vehicles crossing different fluids are simulated by using the software CFX to design cases. Simulation results show that there exists aReinflection point in the flow field during the crossing process, and that,whenReis less than the inflection point, if theReof the air and theReof the water are the same, the change trends of aerodynamic parameters and hydrodynamic ones with the attack angle are consistent and their numerical values are similar, and if theReof the air is close to that of the water,there exists a matching range between flight speed and submerged speed, in which the aerodynamic characteristics are shown to be similar to the hydrodynamic ones. The conclusions can provide a basis for the design of voyage control.

Reynolds number;numerical simulation;aerodynamic characteristic; hydrodynamic characteristic

2014- 11- 03

国家自然科学基金面上项目(61472441) Foundation item: Supported by the National Natural Science Foundation of China(61472441)

杨海燕(1972-)，女，博士，副教授，主要从事航行体设计与仿真研究.E-mail: yanghy07@yeah.net

1000- 565X(2015)11- 0127- 06

V 211

10.3969/j.issn.1000-565X.2015.11.018