基于度序列的复杂网络模型及其路由策略分析*
熊云艳 肖文俊 毛宜军 赖正文 韩冬
(1.华南理工大学 计算机科学与工程学院, 广东 广州 510640; 2.华南理工大学 软件学院, 广东 广州 510006;3.华南农业大学 数学与信息学院, 广东 广州 510642)
基于度序列的复杂网络模型及其路由策略分析*
熊云艳1肖文俊2毛宜军3赖正文1韩冬1
(1.华南理工大学 计算机科学与工程学院, 广东 广州 510640; 2.华南理工大学 软件学院, 广东 广州 510006;3.华南农业大学 数学与信息学院, 广东 广州 510642)
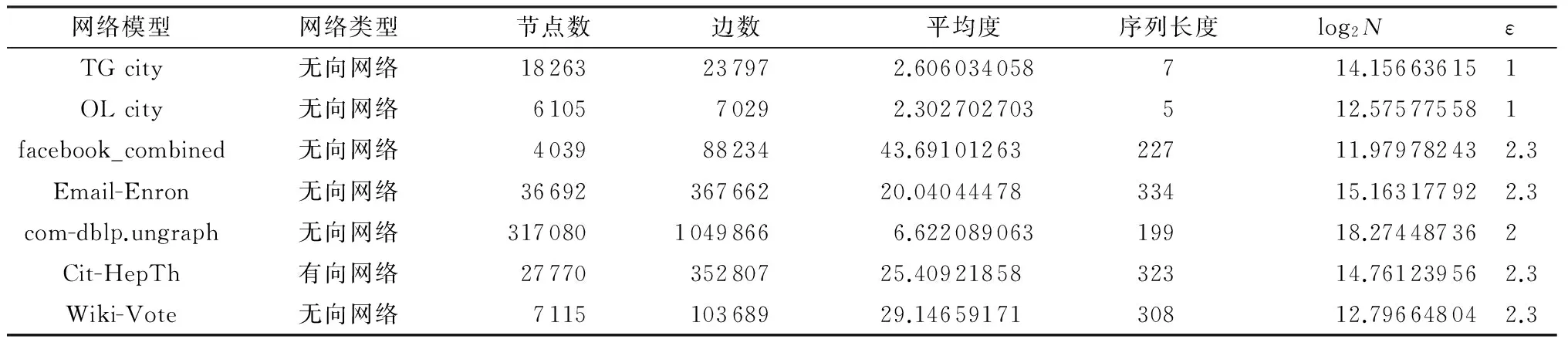
通过对复杂网络一般模型的节点度序列{k1,k2,…,kl}(1≤k1 复杂网络;节点度序列;路由策略 复杂系统主要包括系统单元以及系统单元之间的关联关系.以图论为理论基础的复杂网络是刻画复杂系统的主要工具.复杂网络不仅可以描述复杂系统的静态特性,还可以描述复杂系统的动态演化行为.目前,复杂网络的网络特性、理论证明、实证研究与动态演化等是复杂网络研究中的热点. 从网络特性的角度,复杂网络大致可以分为小世界网络、无标度网络、可导航网络3大类.现实生活中的社交网络、信息网络、技术网络、生物网络都是复杂网络.典型的复杂网络模型包括小世界网络(Small-World Networks)模型[1]、无标度网络(Scale-Free Networks)模型[2]、可导航网络(Navigable Networks)模型[3]和以这3种网络模型为基础衍生的其他各种模型.小世界网络模型采用了随机重连的机制,无标度网络模型中的BA模型采用了增长和优先连接的机制,可导航网络模型则利用网络的局部信息实现复杂网络的可导航功能.文献[2]中提出,复杂网络的度分布满足幂律分布,即P(k)=ck-γ(这里k表示网络的度,c、γ是常量);对于现实生活中的大部分复杂网络,参数γ需满足γ≥2.3[4- 7]. 网络的主要性能参数包括拥塞率、抗攻击性、路由效率等[4,8- 9],而路由表的建立效率是衡量网络路由性能的关键参数之一.路由表的建立依赖于具体的网络模型,即不同的网络模型,路由表的建立算法是不同的.复杂网络中路由表的建立算法包括广度优先搜索(BFS)算法、最大度(MD)算法[10- 12]等. 文中基于复杂网络度序列长度的理论和复杂网络模型,提出了一种基于度序列的复杂网络模型的构建思想.该模型兼顾了小世界网络和无标度网络的特点,同时验证了基于最大度的路由表构建算法比基于广度优先的路由表构建算法具有更好的性能,由此可证明复杂网络中采用基于最大度算法的路由策略是有效的. 无权的复杂网络可以通过有向图或者无向图G(V,E)来描述,其中V表示复杂网络的顶点集合,E表示复杂网络的边集合.描述复杂网络的主要有以下参数: M:复杂网络的边的数量,M=|E|; N:复杂网络的节点的数量,N=|V|; d(v):节点v的度,vV; nk:度为k的节点的数量,nk={v|d(v)=k}; P(k):度的分布概率或者度为k的节点所占总节点的比例,P(k)=nk/N; l:节点度序列{k1,k2,…,kl}的长度,其中1≤k1 在笔者前期的研究中,假定复杂网络的度序列为1≤k1 (1) i=1,2,…,l.文献[13- 15]证明了度序列的长度满足如下结论:当γ>1时,l是log2N级别的,即 l≤O(log2N) (2) 式(2)表明:无标度网络中度序列的长度l相比节点数N是非常小的,基于无标度网络度序列长度的特征,可以重新构建无标度网络的模型. 2.1 度分布为混合分布的度序列 通过式(2)的推导,对于无标度网络,相比网络节点的数量,无标度网络度序列长度非常小.考虑更一般的复杂网络,假设无权的复杂网络可以通过有向图或者无向图G(V,E)来描述,并假设度分布符合幂律与指数的混合分布,其分布函数为 (3) 式中,q为常数. 同理,c是归一化的常量,当i=1时,由式(3)可得 (4) 把式(4)代入式(3),可得 (5) 由式(3)和(5)可得 (6) 当i=1时,可得 (7) 对于等式(7),左右两边取以2为底的对数,可得 (l-1)log2q≥(l-1)log2q (8) 即 (9) 从式(9)可知:当q=2时,式(9)与式(2)的结论是一致的;当q>2时,因为q为常数,log2N/log2q≈(log2N)ε,式(9)可表示为l≤(log2N)ε,可知l与log2N是同级别的.这表明尽管复杂网络的节点数量比较大,但是复杂网络的网络直径是小于(log2N)2的.基于这个特征,如果采用最大度查找算法,则从最小度节点到最大度节点的链路长度一般是小于(log2N)2级别的. 基于上述推导构建基于度序列长度的复杂网络模型,具体步骤如下: 步骤1 按照度的分布函数生成度序列,即{k1,k2,…,kl}. 步骤2 对每一个度序列值ki(ki>3)生成nki个不同的节点(度为1的节点除外),每个节点创建ki个未连接到其他节点的连边(称为半连接),把度相同的节点标识为同一类簇,实现簇内及簇间连接的规则如下: if(nki>ki){ c=nki/ki; r=nki%ki; 先构成c个簇,每个簇内的所有点两两相连,形成一个圈,整个簇对外留下ki个半连接; 剩余r个点两两相连,未能连接的半连接待步骤4补充; }else{ nki个点两两相连,未能连接的半连接待步骤4补充; } 步骤3 簇与簇之间通过半连接相连,保证不同的点之间最多只有一条边,并且没有自环,这样可能会留下一些半连接还没有连接. 步骤4 步骤3中没有连接的半连接与度为1的节点进行连接,最终形成一个复杂网络模型. 2.2 数据验证 BA模型[2]是复杂网络的主要模型,其构建思想如下: (1)增长:网络中有m0个节点,每个步骤t新加入一个节点,该节点与网络中的m个节点连接,满足m≤m0; (2)优先连接:新加入的节点与网络中节点按照如下概率连接: (10) 结合BA模型与第2.1节的度序列模型构造思想,分别构造100、1 000、10 000个节点的BA模型,重复100次试验,去掉非连通分支后,得到的结果如表1所示. 表1 BA模型参数1) 1)BA(1 000,3)表示该BA模型初始有3个节点,每个步骤优先连接已有的3个节点,经过一定的演化步骤后,最终形成具有1 000个节点的网络,余类同;ε为公式(9)的参数. 在http:∥snap.stanford.edu/data/index.html下载Wiki-Vote、Cit-HepTh、Email-Enron、facebook_combined数据集,在http:∥www.cs.fsu.edu/~lifeifei/SpatialDataset.htm下载TG city和OL city数据进行验证. 通过仿真得到表2所示数据. 表2 实证结果 在复杂网络中,参数γ满足γ≥2.3,但是当ε>2时,(log2N)ε随着N增加较快,因此ε不会很快增加,由表1、2的实验数据,可以得出ε≤2.3,因此ε≤γ,而且,(log2N)ε相比N是非常小的. 利用复杂网络度序列的这个特点,可以构建基于度序列的复杂网络模型.该模型中,当度大于3时,把相同的度集中在一个族上,度为1与2的节点属于某个节点族的边缘,不同的节点族之间通过族头连接,从而构成了一个基于度序列的复杂网络模型. 3.1 路由策略 设图为G,节点个数为N,源节点和目标节点分别为i和j,由前面的推导可以得出一般实际网络的度序列长度l是log2N级别的,从最小度节点到最大度节点的链路长度是(log2N)2级别的.路由表构建效率是评价大规模复杂网络中路由策略的关键指标之一,文中通过仿真实验,对比了BFS算法、MD算法、优化的最大度(MD+)算法在构建路由表时的效率.其中BFS算法为传统的基于广度优先的Dijkstra算法,MD和MD+的算法思想分别如下: (1)MD算法 从前面的分析可知,如果采用基于最大度的路由算法,可以建立基于最大度的复杂网络路由表,具体步骤如下: 步骤1 从源节点i出发,判别自己邻居节点中有无目标节点j;如无,则将其中度最大的邻居节点设为当前的节点;如有,则停止查找. 步骤2 可以多次访问同一个节点,但是同一条边只能被访问一次,如果与当前节点相连的所有边都被访问过,则返回上一节点. 步骤3 重复步骤1和2,直到当前节点为目标节点的任一个邻域节点,目标节点即被找到,查找完成. (2)MD+算法 MD算法中没有存储查找的路径,MD+算法则存储了每次的查找路径,即在查找的过程中MD+算法会存储已经查找到的节点之间的路径.具体操作时,在MD算法步骤1的基础上,如果有查到的目标节点就直接使用,否则按照最大度随机选择. BFS、MD、MD+算法的性能分别利用它们得到任意2个节点之间最短路径的查找总次数来评估. 3.2 仿真结果 使用Python编程语言,应用Networkx复杂网络程序包,结合文中提出的一般复杂网络模型的度序列特点进行仿真.为了更加符合现实模型,仿真模型采用了扩展的BA模型,即2.2节中BA模型的参数m是变化的,其满足函数m=mtθ,0≤θ<1.在构造变m的BA模型时,采用了基于度序列的构造思想. 按照2.1节所述度序列模型生成算法,结合变m的BA模型思想,分别生成了10、50、100、500、1 000个节点的网络模型,重复100次实验,得到3种算法的性能数据(如表3所示). 表3 3种算法构造路由表时的性能 从表3可以看出,在复杂网络环境下,BFS、MD、MD+3种算法的性能中,最好的是MD+,其次是MD,最差的是BFS,这证明基于最大度的算法在复杂网络模型下是实用的,且MD、MD+算法同网络的平均度有关.网络平均度越高,最大度算法的优势越明显. 文中利用复杂网络幂律的特性,得出了复杂网络一般模型的度序列长度l与log2N是同级别的结论,并通过模拟仿真与动态数据进一步验证了该结论.基于该结论,对BFS、MD、MD+3种算法的性能进行了仿真对比,结果表明:在复杂网络环境下,相比于传统的基于广度优先的BFS算法,基于最大度的算法其性能有所提升.后续研究中将进一步探讨复杂网络基于最大度算法的动态性能,如网络稀疏度以及拥塞控制等. [1] Watts D J,Strogatz S H.Collective dynamics of “small-world” networks [J].Nature,1998,393(6684):440- 442. [2] Barabási A L,Albert R.Emergence of scaling in random networks [J].Science,1999,286(5439):509- 512. [3] Kleinberg J M.Navigation in a small world [J].Nature,2000,406(6798):845. [4] Strogatz S H.Exploring complex networks [J].Nature,2001,410(6825):268- 276. [5] Pastor-Satorras R,Vespignani A.Epidemic spreading in scale-free networks [J].Physical Review Letters,2001,86(14):3200- 3203. [6] Albert R,Barabási A L.Statistical mechanics of complex networks [J].Reviews of Modern Physics,2002,74(1):47- 91. [7] Newman M E J.The structure and function of complex networks [J].SIAM Review,2003,45(2):167- 256. [8] Arrowsmith D,Di Bernardo M,Sorrentino F.Effects of variations of load distribution on network performance [C]∥Proceedings of IEEE International Symposium on Circuits and Systems(ISCAS 2005).Kobe:IEEE,2005:3773- 3776. [9] Goh K-I,Kahng B,Kim D.Universal behavior of load distribution in scale-free networks [J].Physical Review Letters,2001,87(27):278701/1- 4. [10] Wu J,Tse C K,Lau F,et al.Analysis of communication network performance from a complex network perspective [J].IEEE Transactions on Circuits and Systems I:Re-gular Papers,2013,60(12):3303- 3316. [11] Echenique P,Gómez-Gardees J,Moreno Y.Improved routing strategies for Internet traffic delivery [J].Physical Review E,2004,70(5):056105/1- 4. [12] Wang W X,Wang B H,Yin C Y,et al.Traffic dynamics based on local routing protocol on a scale-free network [J].Physical Review E,2006,73(2):026111/1- 7. [13] Xiao W J,Jiang S Z,Chen G R.A small-world model of scale-free networks:features and verifications [J].Applied Mechanics and Materials,2011(50/51):166- 170. [14] Xiao W J,Chen W D,Parhami B.On necessary conditions for scale-freedom in complex networks,with applications to computer communication systems [J].International Journal of Systems Science,2011,42(6):951- 958. [15] Xiao W,Liu Y,Chen G.Characterizing vertex-degree sequences in scale-free networks [J].Physica A:Statistical Mechanics and its Applications,2014(404):291- 295. A Degree Sequence-Based Complex Network Model and Its Routing Strategy Analysis XiongYun-yan1XiaoWen-jun2MaoYi-jun3LaiZheng-wen1HanDong1 (1.School of Computer Science and Engineering,South China University of Technology,Guangzhou 510640,Guangdong,China;2.School of Software Engineering,South China University of Technology,Guangzhou 510006,Guangdong,China;3.School of Mathmatics and Informatics,South China University of Agriculture,Guangzhou 510642,Guangdong,China) By analyzing the lengthlof the vertex-degree sequence {k1,k2,…,kl} (1≤k1 complex network;vertex-degree sequence;routing strategy 2015- 04- 15 国家自然科学基金资助项目(61170313) Foundation item: Supported by the National Natural Science Foundation of China(61170313) 熊云艳(1976-),女,博士生,副教授,主要从事复杂网络、数据中心网络等的研究.E-mail: yunyanx@163.com 1000- 565X(2015)11- 0030- 05 TP 393.0 10.3969/j.issn.1000-565X.2015.11.0051 相关工作

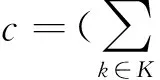
2 复杂网络度序列的一般特征

3 基于度序列的复杂网络模型路由策略

4 结语

