共轭梯度法在GPU及Xeon Phi下的并行优化及比较*
黄敏 丁萍, 罗海飚
(1.华南理工大学 软件学院, 广东 广州 510006; 2.广州中国科学院软件应用技术研究所 智能视频实验室, 广东 广州 511458)
共轭梯度法在GPU及Xeon Phi下的并行优化及比较*
黄敏1丁萍1,2罗海飚2
(1.华南理工大学 软件学院, 广东 广州 510006; 2.广州中国科学院软件应用技术研究所 智能视频实验室, 广东 广州 511458)
为了充分利用多核处理器的强大计算能力并满足具有高并行度应用的需求,提出一种基于大规模稀疏矩阵特征问题求解的并行共轭梯度算法.对图形处理器(GPU)上的计算,有效利用GPU多层次的存储器体系,采用线程与矩阵映射、数据合并访问、数据复用等优化手段,并通过高效的线程调度来隐藏全局存储器的高延迟访问;对Xeon Phi处理器上的计算,有效利用Xeon Phi的高并行度计算对数据通信/传递、减少数据依赖、向量化、异步计算等进行优化,并通过高效的线程调度来隐藏全局存储器的高延迟访问.文中还通过实验验证了算法的可行性和正确性,并对比了不同方式下的运行效率,发现共轭梯度法在GPU下比在Xeon Phi下的加速效果更好.
共轭梯度法;图形处理器;Xeon Phi;并行优化;稀疏矩阵向量乘
城市大气污染的湍流模拟[1- 2]、视频处理、流体和力学计算、生物医药分析等科学计算中牵涉到很多大规模数值模拟,传统的串行计算方式无法满足大规模数值模拟对计算速度的要求,如何提高求解速度是科研人员关注的焦点[3].在城市空气污染的湍流模拟中,如何高效求解预条件方程是提高迭代求解共轭梯度算法性能的关键[4].本研究的应用背景是模拟城市区域多尺度的百万网格的计算[5- 6],在建立有限元的数值模型后,采取雅可比迭代法[7- 8]求解大型稀疏矩阵线性方程组[9- 10].已有实验结果表明,稀疏矩阵向量乘[11](SpMV)占了算法计算总时间的80%以上[12],成为整个计算过程的瓶颈[13].
目前国内外高性能的并行计算主要基于多个中央处理器(CPU)[14],作为底层计算的稀疏矩阵向量乘和线性方程组也不例外.国内外的很多研究都是基于多CPU处理器下的SpMV和线性方程组的并行优化[15].针对不同的稀疏矩阵的特征,有学者提出了适宜的存储格式,这些存储格式可以节省存储空间或加速读取[16].此外,数据预取、分块技术、数据复用和矩阵重组等优化技术也可以应用于其中[17].袁娥等[18]通过将稀疏矩阵分成一个个小的稠密块,使之适宜用块压缩存储(BCSR)格式进行存储,同时采用了寄存器分块和启发式分块大小选择算法,使得该SpMV计算内核的性能大为提高.
由于图形处理器(GPU)的性能得到较大提高,一些研究者开始探讨稀疏矩阵向量乘和线性方程组在GPU上的优化,目前这方面的研究已经比较成熟,例如,Bell等[19]检验了并列格式(COO格式)、行压缩存储格式(CSR格式)和ELLPACK格式(ELL格式),提出了新的混合格式(HYB格式),且在公共测试集上验证了所提格式相对于其他格式的有效性和优越性.Yuan和孙相征等[20- 21]在研究非零元素值被限制在少量的矩阵对角线上的情况时,针对同时具有“带状”性质的稀疏矩阵,提出和实现了一种高效的矩阵向量乘存储格式——bDIA格式.这种方法适宜于每行至多有K个非零值元素的M×N矩阵的情况.Vazquez等[22]发现ELLPACK格式更适合存储.刘杰等[23]在求解稀疏线性方程组时,研究了共轭梯度法在GPU上的并行实现,发现该方法本身不适宜直接放到GPU上计算,需要进行优化和改进,最终提出了高效求解的方法并加以实现.白洪涛等[24- 25]结合矩阵格式探讨了如何在GPU上优化稀疏矩阵向量乘.吴洋和王迎瑞等[26- 27]研究了基于GPU的针对巨型稀疏矩阵的SpMV并行算法.在稀疏矩阵方面,李佳佳等[28]就如何针对不同稀疏矩阵选择存储格式展开了研究.在目前所研究的格式中,CSR格式[29]是一种流行的、具有一般用途的稀疏矩阵范例,适合于矩阵本身没有明显规律的情形.Li等[30]研究了新的矩阵格式——JAD格式,这种格式将矩阵行进行变换,使之类似于对角线格式,结果显示,采用不完全上下三角矩阵(LU)分解的广义最小残量法求解线性方程组,在NVIDIA TESLA C1060上可达到近4倍的加速.
近几年来,Xeon Phi[31]日益普及.它将多个计算核心整合在一起,形成超多核处理器[32],使计算性能大幅度提升.相比SpMV和线性方程组在GPU上的优化,对已有CPU程序不需要做大的改动,就可利用因特尔众核架构(MIC)的计算资源进行优化,这样就不会造成对原有软件资源的浪费[33].目前关于Xeon Phi的研究主要集中在Xeon Phi的架构和底层研究上,有关共轭梯度法和SpMV在Xeon Phi上应用的研究还很少.Liu等[34]在Xeon Phi上做了有关SpMV并行算法的研究,提出了一种新的稀疏矩阵格式ESB(ELLPACK Sparse Block,这种格式是在ELLPACK格式的基础上进行改进,适用于结构规律的矩阵),并使该矩阵适用于Xeon Phi的架构,达到负载均衡,算例显示SpMV在Xeon Phi Coprocessor Codenamed Knights上相较于在Intel Xeon Processor E5-2680和CUDA(NVIDIA Tesla K20X)上分别达到了3.52和1.32的加速比[35].
文中根据应用问题的非结构网格所产生的稀疏矩阵的特点,针对现代异构模式多层次的高性能计算机体系架构,探讨新的稀疏矩阵存储格式和高效的稀疏矩阵向量乘并行算法,综合采用分块技术、矩阵重组、预先提取数据等针对CPU处理器的优化手段,同时,对GPU处理器上的计算采用线程与矩阵映射、数据合并访问、数据复用等优化手段,有效利用GPU多层次的存储器体系,并通过高效的线程调度来隐藏全局存储器的高延迟访问;对Xeon Phi处理器上的计算,有效利用Xeon Phi适于解决逻辑比较复杂且并行度高的问题的优势.文中主要从以下几个方面对Xeon Phi上的并行程序进行优化:数据通信/传递、减少数据依赖、向量化、异步计算等;在此基础上,使用其高效的线程调度来隐藏全局存储器的高延迟访问;最终通过对比GPU、OpenMP和Xeon Phi这些不同方式下的计算效率,结合文中的应用背景,提出适合求解SpMV和线性方程组的并行算法.
1 问题描述和算法改进
文中所研究的应用问题的实验数据集源自城市大气污染项目[5],采集到的数据构成的稀疏矩阵规模约为310 000×310 000,数据类型为双精度浮点型.由于数据量大,若一次性传输这些数据,所耗费的时间和空间对于实验分析而言过于庞大,且在传输过程还会出现数据遗漏的情况.为了实验的准确性和高效性,文中采用基于消息传递接口(MPI)的网格预处理方法对网格方程组进行区域分裂并行计算[1].在对网格方程组进行区域分裂后,将巨型稀疏矩阵划分为若干进程下较小的稀疏矩阵,在此基础上,文中需要解决快速求解大型线性方程组的问题.共扼梯度法是求解大型稀疏线性方程组的有效方法之一[7],文中采用共轭梯度法[8]并通过求解泊松方程组来验证所提方法的有效性.
算法描述如下:
Compute r(0)=b-Ax(0)for some initial guess x(0)
for i=1,2,…
solve Mz(i-1)=r(i-1)
ρi-1=r(i-1)Tz(i-1)
if i=1
p(1)=z(0)
else
p(i)=z(i-1)+βi-1p(i-1)
end if
q(i)=Ap(i)
x(i)=x(i-1)+αip(i)
r(i)=r(i-1)-αiq(i)
check convergence;continue if necessary
end
结合文中的应用背景,优化后的共轭梯度法在GPU上的求解流程如下.
步骤1 CPU端读取矩阵文件,GPU从CPU端获取稀疏矩阵数据和向量文件.
步骤2 在CPU端将不完整CSR格式存储的数据提取出来,转换为完整CSR格式,从而解除计算中的原子操作.
步骤3 计算残差r(i)=b-x(i)(i=0,1,2,…).
步骤4 交换不同节点边界的残差.
步骤5 得到雅克比系数diagonal_diff=M-1.
步骤6 在CPU运算平台求出迭代矩阵.
步骤7 计算SpMV:q=A×p,其中q表示稀疏矩阵和向量乘积的结果.
步骤8 计算全局误差:Error=sum(rr×rr),其中rr为标准差.
步骤9 求解x的值,检验是否符合精度要求或者是否已经达到最大迭代次数,从而确定迭代是否终止.若条件成立,x即为方程的解向量,否则转步骤3.
步骤1读取矩阵数据和格式转化,运算一次即可,故在CPU端执行该步骤运算.步骤5和6涉及多次迭代,也是整个迭代运算的核心,需要在GPU上进行优化.步骤7中的矩阵向量乘是整个方程求解中运算量最大的部分,该步骤需要在GPU上重点优化.
最后将获得的解向量由GPU传送至主机内存中.
上述步骤共涉及稀疏矩阵与向量相乘2次、对角矩阵与向量相乘1次、向量与向量相乘2次、向量更新3次、标量相除2次,其中矩阵与向量相乘、向量与向量相乘、向量更新都可以利用数据级的并行操作,从而可以实现在CUDA和XeonPhi上的并行计算[7,35].上述流程中,SpMV的计算时间占了总计算时间的80%以上[12].SpMV计算性能与所计算的矩阵有直接的关系,矩阵的规模、分布情况、稀疏程度以及非零元素个数等都会影响加速效率.文中所研究项目来源于针对城市空气污染模型的大涡模拟,其通过网格并行划分后产生的稀疏矩阵的非零元素值大致走势的Matlab仿真图如图1所示.可见,稀疏矩阵呈对称正定线性分布,而非分块或条形对角线分布,除了对称外,不具有某种特殊格式.文中采用更加灵活且易于操作的CSR格式,并在此格式基础上进行改进和优化.
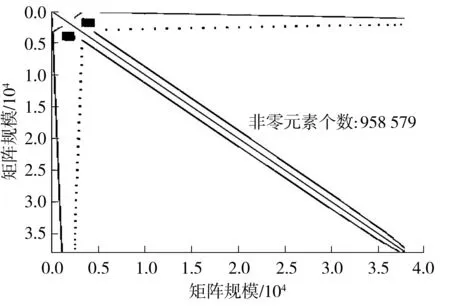
图1 稀疏矩阵非零元素分布图Fig.1 Distribution diagram of non-zero elements of sparse matrix
CSR[29]用3个相关向量来表示稀疏矩阵,其中向量A用于存储稀疏矩阵的非零元素,向量Col_A用于标识非零元素对应的列值,向量Row_A用于存储每一行第1个非零元素的偏移量,即Row_A[i]表示第0行到第i-1行的非零元素个数和,初始Row_A[0]赋值为0.对于一个M×N的稀疏矩阵,Row_A向量的长度为M+1,其作用是把每一行的偏移量存到Row_A[i]中,其最后一个元素存储矩阵中非零元素的个数.图2示出了如何用CSR格式中的3个一维数组表示稀疏矩阵的过程.
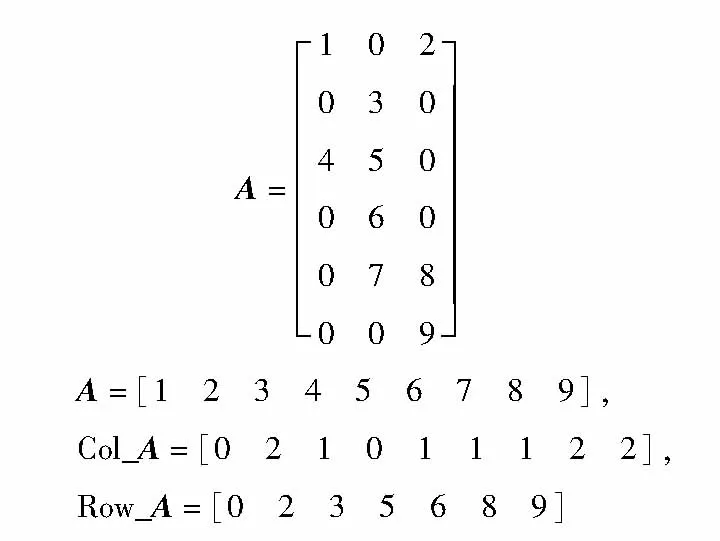
图2 CSR范例
1.1 基于GPU的SpMV的Kernel函数
计算机GPU体系架构在不断发展,文中以NVIDIA Tesla K20[16]体系架构为代表对GPU的并行层次进行分析.NVIDIA Tesla K20由可伸缩流处理器阵列(SP)和存储器系统组成,并由一个片上的互联网络连接.GPU利用大量功能简单的流多处理器协同运算来提高数据的吞吐率和计算速度.与之不同的是,CPU则采用相对复杂的分支预测和逻辑控制来迅速获得数据和指令,从而减少了延迟带来的耗时.GPU在计算时,是以线程(Thread)为单位,每个线程有本地内存和多个寄存器(Register).其一个线程块(Block)由若干个线程组成,各线程块中的线程可以通过共享内存进行通信,多个线程块组成了一个线程网格(Grid).针对GPU的体系架构可以分析出:基于GPU平台的稀疏矩阵向量乘方法存在的挑战主要包括线程映射和存储层次的管理、数据访问和数据复用、非零元素分布不均.
常见的基于CSR格式、利用CUDA加速的SpMV有3种实现方法:①使用一个线程来处理一行,一个warp包含32个线程,那么一次可以处理32行,但因每行非零元素个数的不同,线程空转的问题会非常严重,同时,在线程空转情况下,无法联合访问GPU的显存,降低了访存效率;②每个线程块计算结果向量的一个元素,同样也会存在每个线程块处理非零元素不均而造成线程空等的情况;③若使用一个warp来计算矩阵的一行与向量乘,虽然在一定程度上减轻了线程空转的问题,并且warp内可联合访问,使得运行效率有所提高,但是空转问题依然比较严重,访问效率仍然存在提高的空间.用CSR进行存储时,基于GPU平台下的SpMV还存在着以下问题:第一,线程间等待的问题可能是由于同一个warp内的线程间的计算量负载不均衡而引起的;第二,线程不满足对全局存储器的合并访问导致访存延迟.这两个问题都可能影响到稀疏矩阵方程组的求解性能.结合文中稀疏矩阵的特点,每一行非零元素值不超过32个,故选择第3种方式并在此基础上进行优化.
由于文献[5- 6]中初始程序里的计算方式不是完整CSR格式,而是按照对角线和上三角矩阵来进行计算,若是分别进行存储,再放到GPU上计算,会产生原子操作,从而影响计算速度,所以开始需要扫描一遍稀疏矩阵,生成完整CSR格式,解除CUDA上的原子操作(1).伪代码如下:
for i<-THREAD_ID to nde ∥nde表示矩阵维度
for k<-nnz[i] to nnz[i+1] ∥数组nnz[]存储每行非零元素个数
tmp_kk<-colume[k] ∥数组colume[]存储非零元素的列下表值
dbl_tmp<-delta_t*diff[k]∥dbl_tmp代表矩阵A的非零元素值
qq_i<-qq_i+dbl_tmp*pp[tmp_kk]∥A*p
atomicAdd((double*)&(temp_qq[tmp_kk]),double(dbl_tmp * pp[i]))∥原子操作(1),避免同一线程块内不同线程对同一元素进行加操作以及同一线程网格内不同线程块内不同线程对同一元素进行加操作
temp_qq[tmp_kk]<-temp_qq[tmp_kk] + dbl_tmp*pp[i]∥数组temp_qq存储A*p的值
end
针对GPU架构上SpMV的计算资源没有充分利用以及负载不平衡等问题,文中对CSR格式进行改良,即采用非零元素个数升序排序,把非零元素个数相似的矩阵行尽可能多地放在一个warp或者多个warp中进行处理,以避免计算资源浪费和解决负载不平衡的问题,进而提高稀疏矩阵向量乘的计算性能.
基于CUDA的稀疏矩阵向量乘的具体优化算法流程如下,其中“2”、“3”-“7”采用异步操作“cudaEventCreate(&start);cudaEventCreate(&stop);”,使申请GPU变量空间和计算误差等步骤同步进行,这样可以隐藏申请GPU变量空间的时间,具体的算法步骤如下:
1 cudaEventCreate(&start)
2 malloc variable space,initial the whole CSR array col_A、row_A、val_A,transfer array col_A、row_A、val_A、q to GPU
3 poisson_solver_residual()∥calculate the residual error
4 exchange the Boundary elements()
5 From initial value x,calculate r=b-Ax
6 p=M-1r and transfer the value p to GPU
7 ρ=rTp
8 cudaEventCreate(&stop)
9 for i=1,2,…{
10 GPU kernel
11 {q=Ap}
12 transfer p and q to CPU
13 CPU {
14 exchange the elements of each boundary();
15 α_tmp=pTq
16 α=ρ/α
17 ρold=ρ
18 r=r-αq
19 e_tmp=rTr
20 q=M-1r
21 ρ_tmp=rTq
22 β=ρ/ρold
23 }
24 exchange the error of each boundary();
25 transfer p and q to GPU
26 GPU kernel {
27 p=q+βp
28 q=val_diag×p
29 x=x+αp
30 }
31 transfer p,q to CPU
32 Check the convergence,end if satisfied
33 end of for
34 end
根据以上描述,文中的算法流程可以用图3来描述.
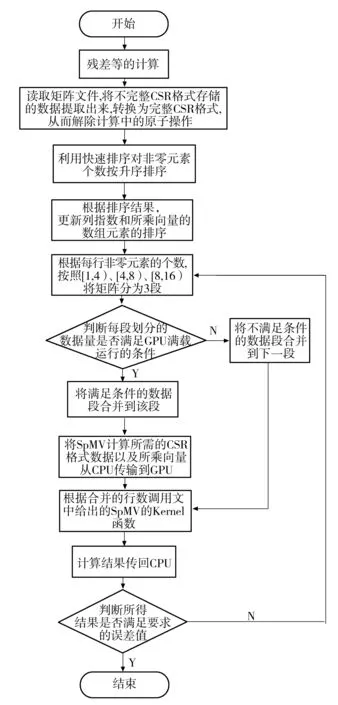
图3 文中优化算法的流程
1.2 基于GPU的SpMV的Half-Warp优化
采用线程负责计算结果向量的一个元素时,因CUDA的体系架构,处理器是将线程块划分为多个warp,并且以warp为执行单元,同一warp内的线程是天然同步的,所以当一个warp内的线程对应处理行的非零元素个数相差较大时,每个线程的进度会有很大的差异,这将造成许多线程计算资源的空转等待.与DIA和ELL格式不同,CSR存储格式每行拥有可变数量的非零元素个数,而这种差异导致了线程间的差异.例如,当稀疏矩阵每行包含高度可变数目的非零元素时,可能会出现的情况是:在包含非零元素个数最多的行的线程继续重复执行操作的同时,同一warp中的其他线程却保持空闲状态.另外,线程的同步会产生额外的开销.若每个线程块计算结果向量的一个元素,当稀疏矩阵某一行的非零元素个数不能被block内的线程总数整除时,也会出现部分线程等待的情况.而矢量内核的有效执行需要矩阵的行包含的非零元素个数大于warp的大小(一般为32).所以,当所计算行的非零元素个数小于GPU的执行单元warp的线程数32时,利用warp计算的策略仍然会存在空转等待的情况.因此,矢量内核的性能与矩阵每一行的非零元素值的个数是紧密相关的.文中研究对象所产生的稀疏矩阵各行中最大的非零元素个数不超过32,且超过70%的矩阵行的非零元素个数不超过16,进一步地结合GPU的全局存储器合并访问的需要,可知文中适合采用Half-Warp的策略.
以Half-Warp为单位循环计算的优化策略即每个Half-Warp分别计算稀疏矩阵中某一行元素与向量的乘积.首先,根据block和grid线程个数的分配以及矩阵行非零元素的个数,动态地将数据以Half-Warp为单位进行分割,每个单位计算稀疏矩阵的一行元素值与向量的乘积,然后对Half-Warp的中间结果进行reduction归约求和,由于中间结果存在数据复用,为了有效地提高寄存器的访问速度,文中使用了共享存储器SharedMemory来存储.文中SpMV的Kernel函数的程序伪代码如下(优化编译选项为-arch sm_35):
t<-threadIdx.x∥Each block’s Thread ID
id<-t &(warpSize-1)∥Thread ID within warp
warpsPerBlock<-blockDim.x/warpSize
myRow<-(blockIdx.x*warpsPerBlock)+(t/warpSize)∥One row per warp
Create shared memory array val[NUM_THREADS]
∥以上为赋初始值
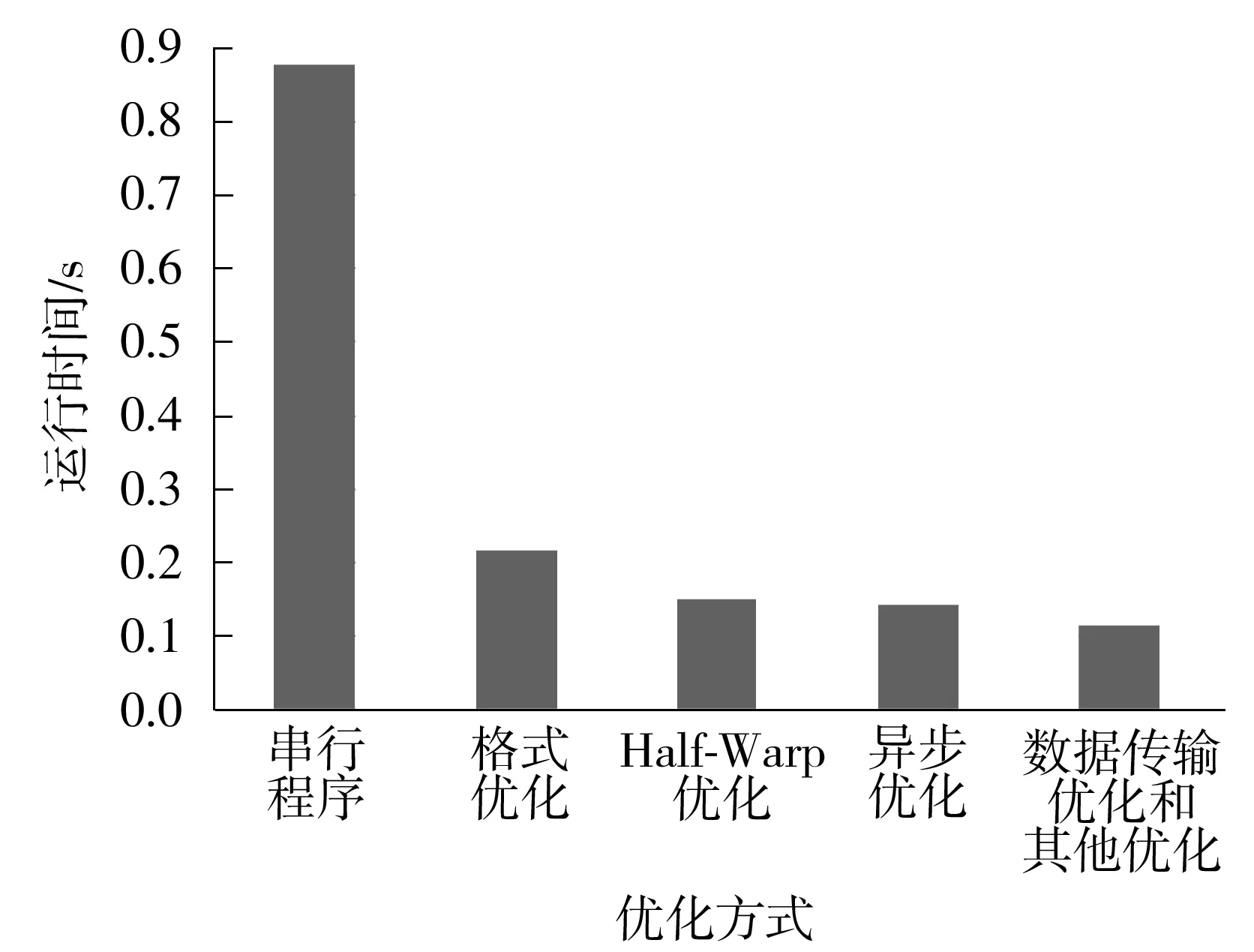
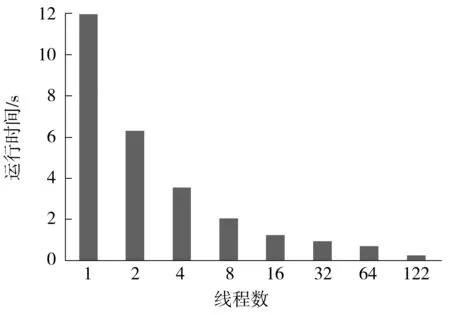
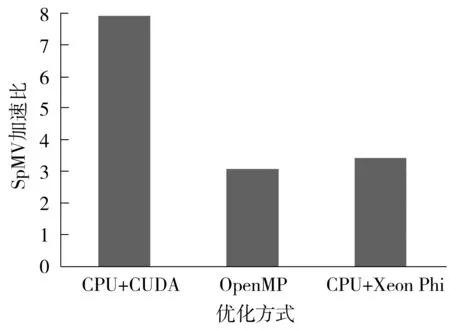
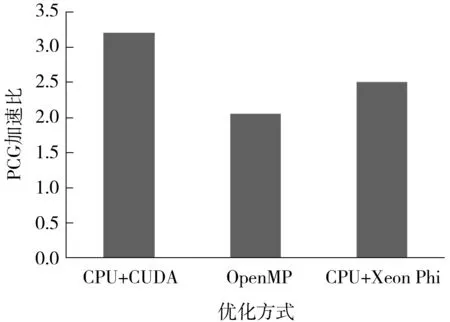
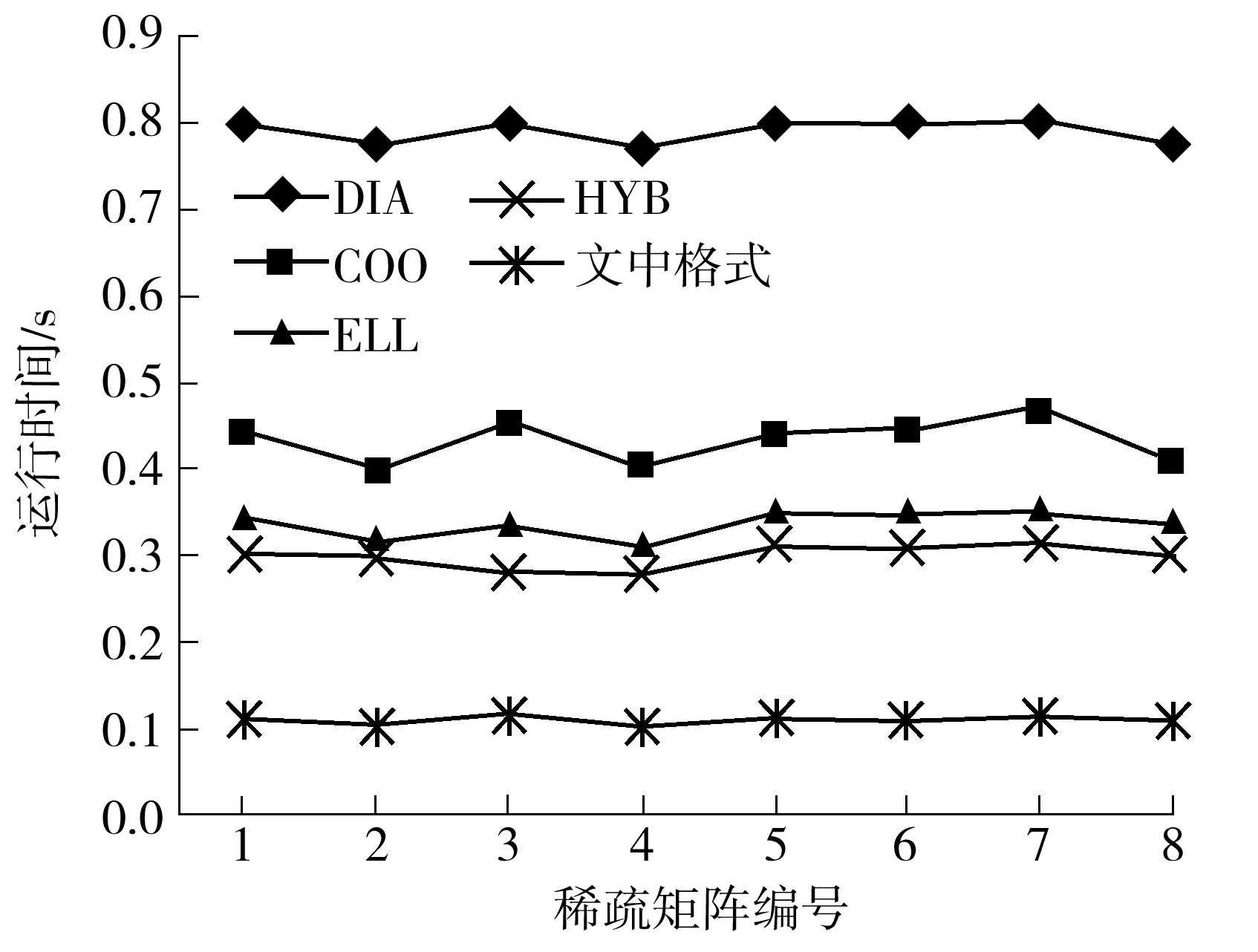
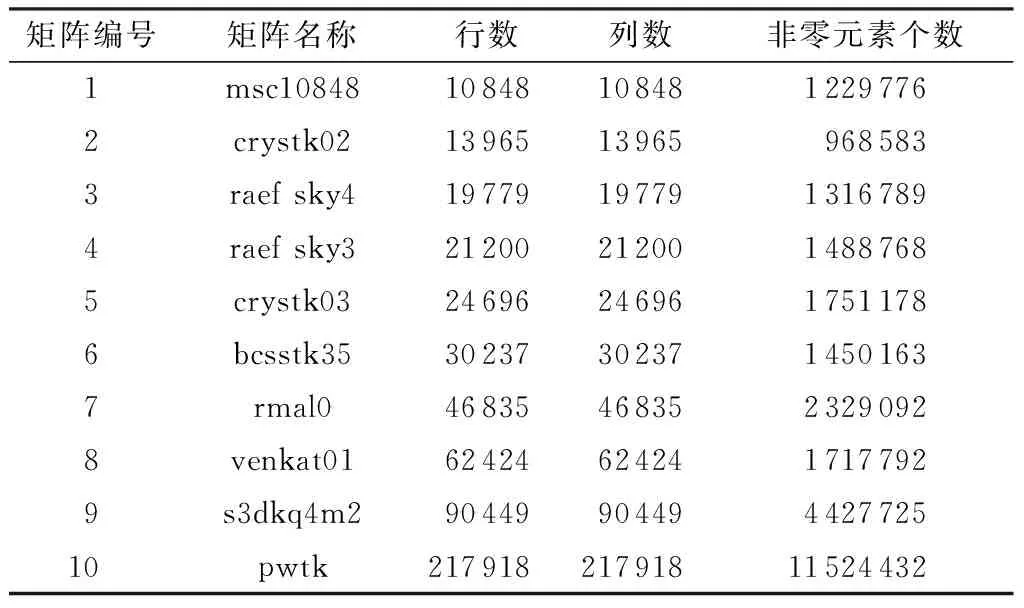
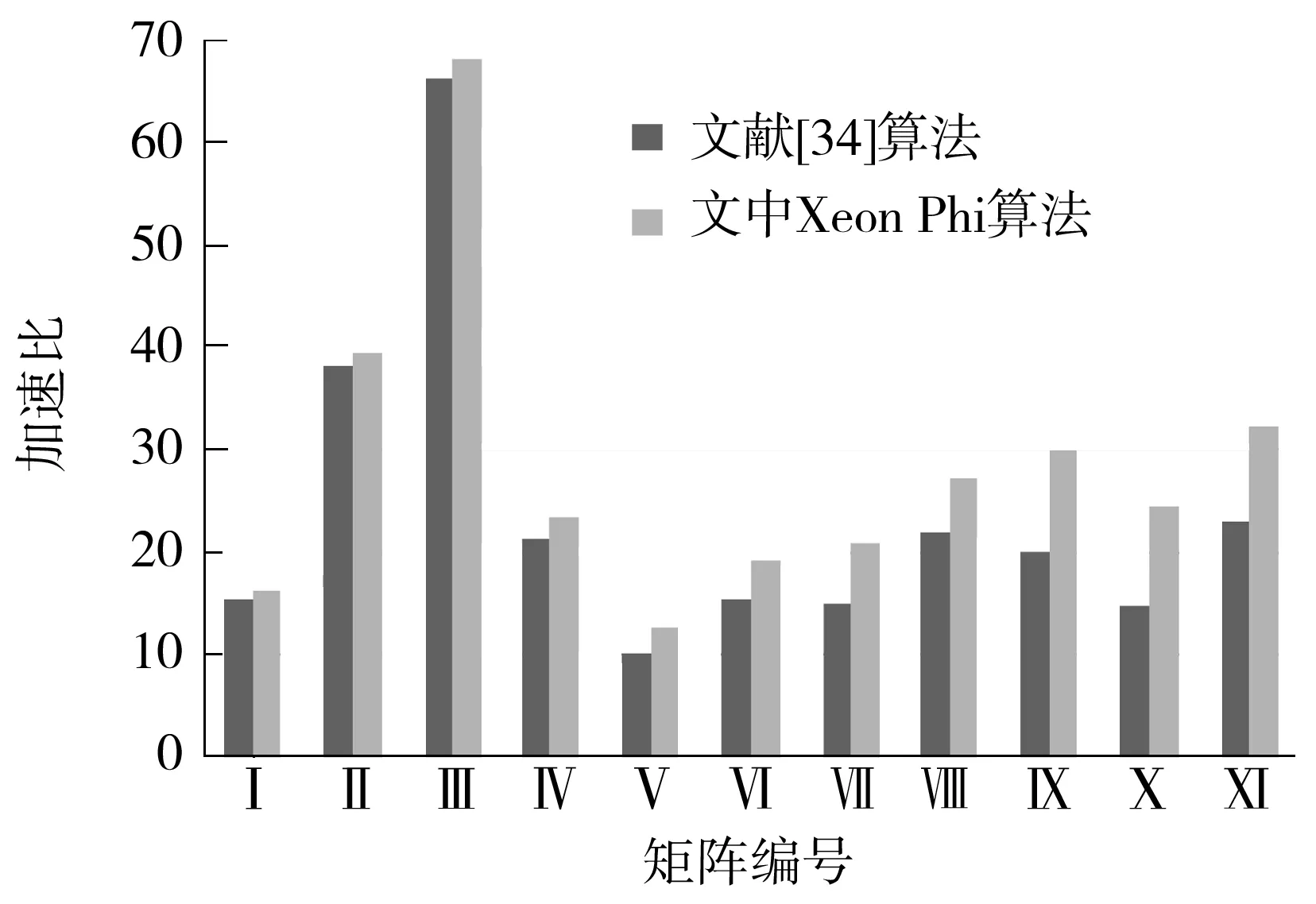
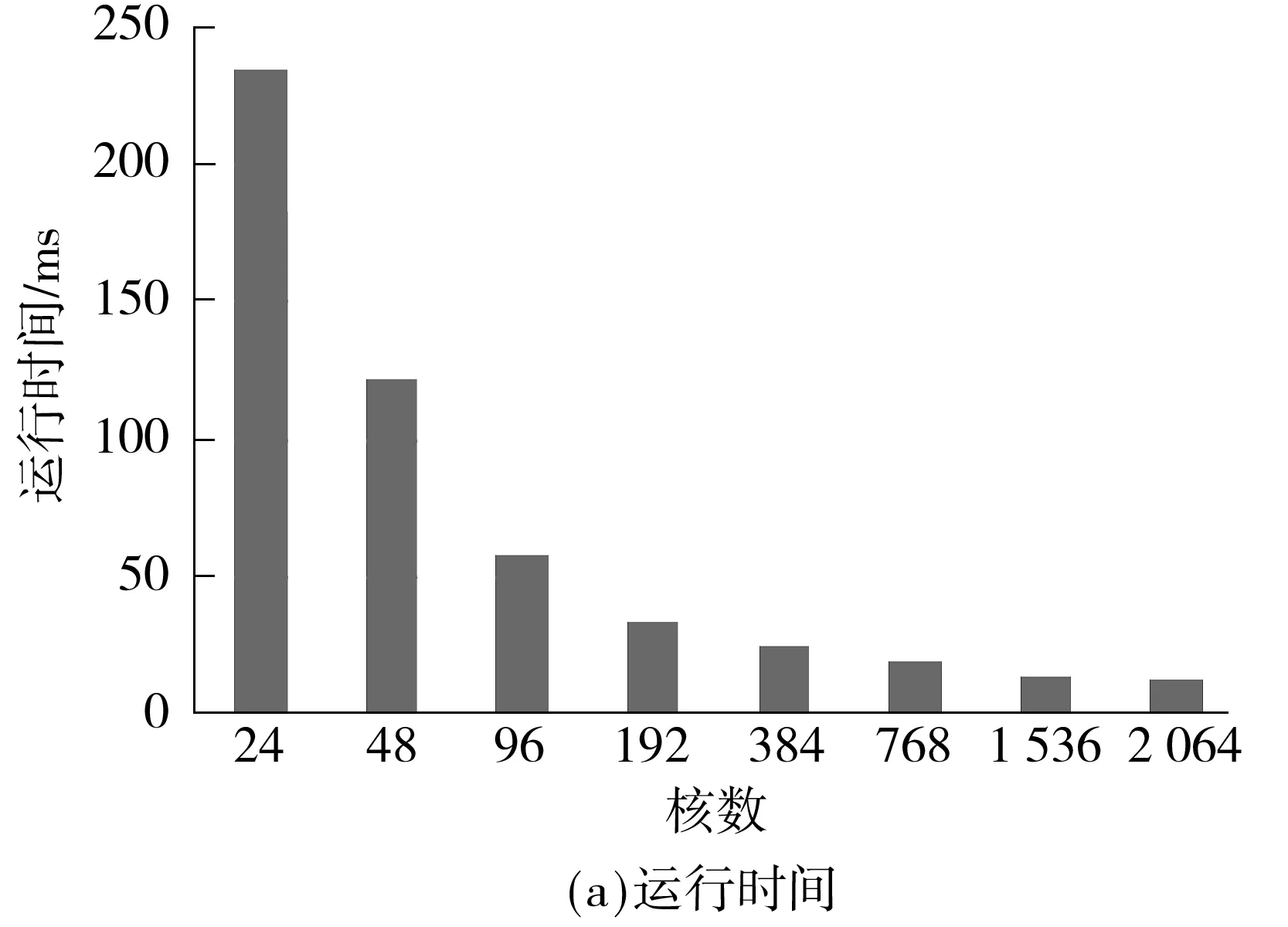
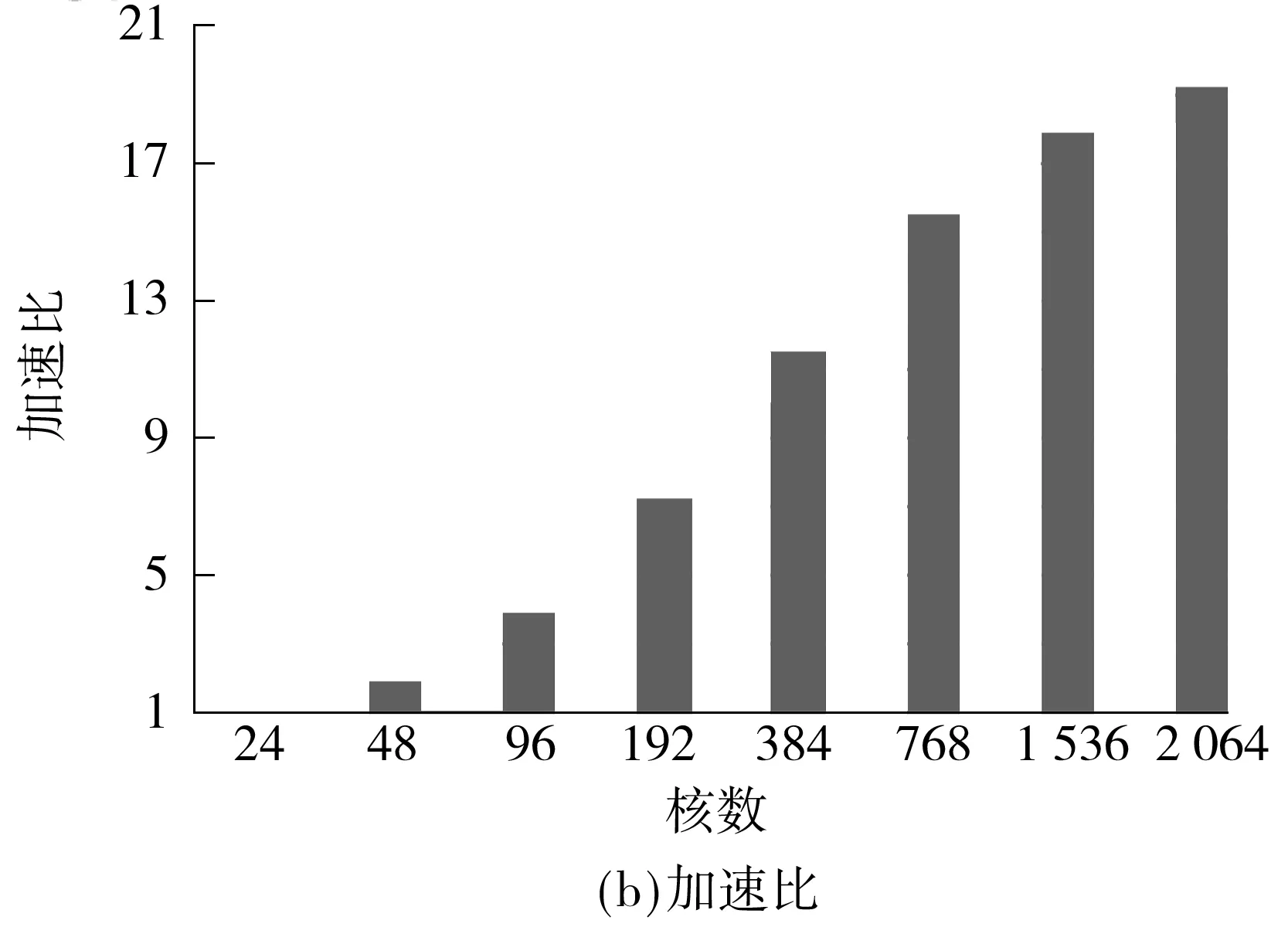
if myRow warpStart<-nnz[myRow] warpEnd<-nnz[myRow+1] qq_i<-0.0 for jj<-warpStart+id to warpEnd tmp_kk<-colume[jj] qq_i<-value[jj]*pp[tmp_kk]+qq_i jj<-warpSize+jj val[t]<-qq_i ∥Reduce the partial sums if id val[t]<-val[t+mun]+val[t] end for ∥Write the result if id==0 temp_qq[myRow]<-val[t]+temp_qq[myRow] end 1.3 数据的传输 在进行GPU通用计算时,有时会出现数据从CPU端传到GPU端的时间比kernel的运行时间要长的情况,而数据的传输又是基于GPU通用计算之外的开销,因此会影响整体的运行速度,进而降低加速比.文中算法采用了分页锁定(Page-Locked)内存空间的方式,用cudaMallocHost()申请一块CPU内存,再将数据拷贝到显存,这样将会减少一定的数据传输时间,从而提高计算速度.但是当数据规模非常大时,在CPU上锁定太多的内存同样会影响kernel的运行时间,所以文中仅用cudaMallocHost()申请需要在CPU和GPU之间频繁传输的中间计算结果pp和qq. 1.4 其他优化 其他优化如下:①两向量点乘的操作和向量更新通过自编kernel函数,采用并行规约求和方法,比直接调用CUBLAS库中的CublasDdot实现点乘运算和调用CublasDaxpy更新向量要快1.6倍;②为了加速数据读取、减少读取延迟,文中用纹理寄存器绑定CSR格式中的val值. 1.5 Xeon Phi优化 1.5.1 并行优化 首先,为了减少开销,文中只进行一次创建和结束OpenMP并行区域的操作.其次,将r、e_tmp、q和ρ_tmρ放在同一个OpenMP循环内,并且把p、q和x放在另外一个循环内,以便使接下来的计算可以从缓存中直接读取数据,文中把r和向量在for循环计算开始前读入高速缓存中.例如,q=M-1r可以从缓存中预先读取下一次计算所需的r值,直到最后一次循环结束.最后,用变量q替换变量z并进行分组计算,这样可以省去变量z在算法中所带来的开销.优化流程如下(所使用的优化选项为-O3): 1 #PARAGMA OMP PARALLEL { 2 for i=1,2,… 3 # PARAGMA OMP PARALLEL FOR 4 q=Ap 5 #pragma omp single {exchange boundary elements} 6 # PARAGMA OMP FOR REDUCTION (+:α_tmp) 7 α_tmp=pTq 8 # PARAGMA OMP SINGLE{ 9 α=ρ/α 10 ρold=ρ 11 } 12 # PARAGMA OMP FOR REDUCTION(+:ρ_tmp,error_tmp){ 13 r=r-αq 14 e_tmp=rTr 15 q=M-1r 16 ρ_tmp=rTq 17 } 18 # PARAGMA OMP MASTER { 19 20 β=ρ/ρold 21 } 22 # PARAGMA OMP SINGLE { 23 exchange the error of boundary 24 } 25 # PARAGMA OMP FOR NOWAIT{ 26 p=q+βp 27 q=val_diag×p 28 x=x+αp 29 } 30 Check the convergence,end if satisfied 31 end of for 32 end of #PRAGMA 1.5.2 减少数据依赖 将上三角格式分别计算、转换为完整CSR格式来计算SpMV,可去掉内层循环的数据依赖关系,即去掉了多线程下的原子操作.对于Xeon Phi平台,由于要开启上百个线程,减少线程开启对平台性能的影响更为重要.在内层计算之前,与上述GPU优化一样,先转换为完整CSR格式并进行排序,在排序的同时将内层循环需要随机调度的变量按顺序存放,以便进行向量化优化,这样可以隐藏线程间的交互时间. 1.5.3 向量化优化 计算误差和更新向量结果值的操作在调整程序循环结构(比如循环嵌套和交换次序等)并使之没有数据依赖关系后,使用自动化向量化优化循环. 1.5.4 计算异步 计算进程从主进程获取初始化后的数据以及稀疏矩阵所要乘的向量的值.申请Xeon Phi变量空间和计算误差、转换数据格式等步骤同步进行,这样可以隐藏在Xeon Phi上申请变量的时间.最后释放Xeon Phi上已申请的空间.为了隐藏数据传输时间,文中以流水线方式执行传输数据和计算,具体如图4所示. 图4 异步执行示意图 文中测试平台如下:CPU为Intel(R) Core(TM) i5-3470 CPU 3.20 GHz;GPU为Nvidia Tesla K20M;Xeon Phi为Intel(R) Xeon(R) CPU E5-2650 0 @2.00 GHz,7 110P,8 GB GDDR5,61 cores;操作系统为64位Linux Red Hat,1个CPU,1个GPU,1个MIC.所测试的数据来源于大涡流模拟有限元计算产生的稀疏矩阵[5- 6],稀疏矩阵用WRF_PCG表示,选取主进程所产生的稀疏矩阵数据作为代表进行测试,它的主要特征参数见表1. 表1 参数设置 首先,在CPU+GPU平台单进程下测试SpMV的运行时间,测试结果见图5. 从图5可看出:格式优化后WRF_PCG在GPU上的运算速度大幅度提升,耗时从串行程序的0.879 s加速至0.214 s,说明将不完整CSR格式转换为完整CSR格式后,所解除的原子操作以及优化数组排序的操作使得WRF_PCG更适合在GPU上进行计算;Half-Warp及数据异步优化、数据传输等其他优化所带来的加速效果分别对应于0.148、0.140和0.111s的耗时.以Half-Warp为单位的计算适合文中稀疏矩阵各行非零元素个数不超过16的情况,在提高寄存器访问速度的同时降低了线程空转的可能;数据异步优化隐藏了在GPU上开辟空间传输数据的时间,数据传输优化和其他优化增强了数据复用;从耗时加速情况来看,文中各种策略是有效的. 图5 WRF_PCG在CPU+GPU下优化后的SpMV运行时间 Fig.5 SpMV run-time of WRF_PCG after CPU+GPU optimization 然后,在CPU下用OpenMP优化后测试SpMV的运行时间,结果如图6所示. 图6 WRF_PCG在OpenMP优化后的SpMV运行时间 从图6可看出,在1、2、4个线程下,OpenMP优化后的加速比基本是随着线程数的增多而接近线性增长,由于测试环境的CPU是4核,每个核2个线程,所以在8个线程开启时,运行加速效果最佳. 最后,在CPU+Xeon Phi下用Xeon Phi优化后测试SpMV的运行时间,结果如图7所示. 从图7可看出,在其他条件相同的情况下,1个线程时Xeon Phi的优化效果并不理想,比CPU单线程下运行慢很多.进一步测试发现,在Xeon Phi上开辟变量空间和数据传输时间对运行速度影响更大.当线程数达到Xeon Phi cores的两倍时,运算时间最短,达0.259 s,与初始程序相比,加速比达3.421,加速效果较为明显.由于启动Xeon Phi卡的耗时过长和线程切换耗时,在Xeon Phi下的优化效果不如NVIDIA Tesla K20. 图7 WRF_PCG在CPU+Xeon Phi优化后的SpMV运行时间 Fig.7 SpMV run-time of WRF_PCG after CPU+Xeon Phi optimization 在其他条件相同,1个GPU卡、1个MIC卡和2个CPU核四线程开启的情况下,WRF_PCG在各优化方式下的SpMV和PCG的加速比情况如图8、9所示.可以看出,对WRF_PCG而言,SpMV和PCG加速效果最好的是CPU+CUDA方式,其次是CPU+Xeon Phi,最后是OpenMP.在百万网格产生的数据量下,CPU+CUDA异构模式在高性能计算机上用共轭梯度求解稀疏线程方程比仅在CPU下求解加速3.2倍,而在整个计算最耗时的计算SpMV部分,加速比约达7.9.随着数据量的增大,CUDA的计算速度会得到更大程度的发挥,所以该算法优化程序的扩展性良好. 图8 WRF_PCG在各优化方式下的SpMV加速比 Fig.8 SpMV speedup ratio of WRF_PCG after each optimi-zation 为了证明文中所选存储格式是最适合的,分别在DIA、COO、ELL、HYB和文中格式下测试文中数据集(相应参数列于表1). 8个进程下稀疏矩阵的非零元素值的分布见图2,测试结果如图10所示. 图9 WRF_PCG在各优化方式下的PCG加速比 Fig.9 PCG speedup ratio of WRF_PCG after each optimization 图10 不同存储格式下运行时间的比较 Fig.10 Comparison of run-time under different storage formats 从实验结果来看,不同存储格式的计算性能有很大的差异,文中所讨论的应用问题所产生的稀疏矩阵的非零元素分布是对称的,但不存在与对角线平行的直线,且有很多离散的点分布,这种分布与对角线格式的要求差异最大,在用对角线格式存储时会填充很多零值,既占据大量存储空间又不能给计算带来便利,故该方法的优化效果最差,较串行算法仅加速10%.COO格式具有普遍应用性,但行和列指针都被显式地存储,开辟的存储空间较其他格式要多,所以其优化效果并不是最佳,较串行算法其加速比约为2;当矩阵每行的非零元素值的最大数目与平均数目相差不大时,ELL格式是比较好的选择,这种格式更适合于规则的矩阵.文中的矩阵形状并不是由半结构化和结构化的网格得到的矩阵抽象图,也不是最适合的格式,较串行算法的加速比约为2.6.HYB格式是将ELL和COO两种格式进行混合,这种格式适合于当稀疏矩阵每行的非零元素值的数目变化特别大时,相比两种单一的格式,其加速效果明显,但文中矩阵的每行非零元素的个数变化不大,所以加速效果没有预期显著,加速比约为3.文中的优化算法是针对应用问题产生的矩阵进行的优化,从GPU的多层次存储器体系、线程与矩阵映射、数据合并访问、数据复用等方面逐一进行分析和优化,并最后达到比较理想的加速效果.虽然不同进程下产生的稀疏矩阵的数据不同,但是其非零元素分布图大同小异,实验结果也进一步证明,在分布情况如图2所示,且矩阵本身没有特别的格式特征,用其他格式也达不到比较好的加速效果的情况下,采用文中的优化算法最佳,其相较于串行算法的加速比约为8. 为了验证文中所提算法的拓展性和有效性,选取与文献[18]相同的10个测试矩阵来测试稀疏矩阵向量乘的性能,测试集来源于佛罗里达稀疏矩阵集[36],该测试集中的数据可以真实地反应SpMV在真实应用中的性能.所选取的10个稀疏矩阵的结构信息如表2所示(按照行列数排序). 表2 稀疏矩阵参数 文献[18]和[28]与文中研究内容相似,因此,在相同测试环境和测试集下,分别根据文献[18]和[28]所提供的算法并将参数调试到其最优情况,测试表2中稀疏矩阵的加速比,结果如图11所示. 图11 3种SpMV算法对10种稀疏矩阵的加速比 Fig.11 Speedup ratios of three SpMV algorithms on ten sparse matrices 从图11可看出:对于3种基于CSR格式的算法而言,若矩阵的结构由单一分块组成(如矩阵1、2、4、5),SpMV的加速比会更大;若矩阵的结构不适宜分块(如矩阵3和7),则SpMV的加速比相对较小.文献[28]和文中算法都采用异步计算的方式,隐藏了转换和优化格式的时间,而文献[18]中算法没有隐藏,其转换BCSR格式的时间使得加速比不如其他两种算法.文中算法在选取参数和应用数据上都是以实际应用为背景,故在应用性上较文献[28]中算法更具有普遍性和有效性,在测试10个不同矩阵时,文中算法从加速比结果来看是最优的. 对文中提出的优化方法在公共稀疏矩阵方程集上进行测试,选用的是文献[36]中的11种不同规模的矩阵.这些矩阵选取自科学和工程计算中常用的矩阵数据,规模由千量级至百万量级,跨度很大.测试矩阵数据来源于流体力学、热能计算、空气动力学、计算机图形学、生物和环境科学等领域,具有不同的非零元素个数和矩阵特征.表3列出了测试矩阵的具体参数. 表3 测试矩阵参数 在相同测试环境和测试数据下,根据文献[15]所提供的算法并将参数调试到其最优情况,测试表3中的稀疏矩阵,文献[15]和文中优化算法在CPU情况下的加速比对比如图12所示. 从图12可看出,两种算法的加速比均大于10,最高达70以上,但从整体来看,文中所提算法的加速比优于文献[15]算法,且矩阵规模越大加速效果越明显.当矩阵规模到达1 585 478×1 585 478时,文中算法的加速比约为文献[15]算法的1.4倍,加速效果显著.另外,文中算法在数据处理时采用分块的方法,且对存储器的优化适用于实际应用数据,故在应用性上较文献[15]算法更具普遍性和有效性. 图12 文中算法和文献[15]算法对测试矩阵的加速比 Fig.12 Speedup ratios of the proposed algorithm and the algorithm proposed in Literature [15] on test matrices 为验证文中提出的基于Xeon Phi的优化算法在其他应用上的可拓展性,测试了该算法在表3中所给稀疏矩阵上的加速比,并与文献[34]中提出的基于Xeon Phi上的稀疏线性系统的优化算法进行比较,结果见图13. 图13 文中算法和文献[34]算法在公共集方程上的加速比 Fig.13 Speedup ratios of the proposed algorithm and the algorithm proposed in Literature [34] on the public equation matrix 从测试结果来看,在Xeon Phi上的整体加速比较在GPU上的略低,这是因为SpMV本身计算的逻辑性并不复杂,而Xeon Phi中开启线程和线程间的开销比计算所需时间要多.文中算法整体加速比均大于10,最优情况达到68.14,总体而言,文中算法优于文献[34]算法,同时随着矩阵的规模增大,文中算法的加速效果愈发明显.当矩阵规模为4 307×4 307时,文中算法较文献[34]算法的加速比增加约6.4%;当矩阵规模达到1 585 478×1 585 478时,文中算法加速比约为文献[34]算法的1.5倍,加速效果显著.在所测试的11个不同矩阵上,文中算法均获得了更好的加速效果. 为了说明文中算法的可扩展性,在广州超级计算中心的天河二号超级计算机上,根据应用问题和超级计算机硬件的特性设计计算参数,用现代并行理论评测工具测评并行程序,找出问题瓶颈,实现程序的大规模测试优化.不同节点数时文中算法在GPU上的运行时间和加速比如图14所示.可见,在2 064核上仍有加速,加速比近20,表明文中算法具有良好的可扩展性. 图14 文中算法在天河二号超级计算机上的超多核测试结果 Fig.14 Test results of the proposed algorithm on the Tianhe-2 supercomputer under many-core condition 文中针对并行共轭梯度应用问题中的存储器瓶颈类算法SpMV进行研究,将问题的特征与GPU的特殊体系结合在一起,提出了CSR格式下的优化策略,实验结果验证了文中方法的有效性;同时,进一步分析OpenMP版本的性能结果,证实了在Xeon Phi上优化的可能性.由于OpenMP版本的性能结果良好,移植到Xeon Phi上并进行各种优化后,已达到预期的优化效果.对比CUDA和Xeon Phi的实验结果不难发现,对于随机存储性大且并行度不高、逻辑简单的应用而言,CUDA比Xeon Phi更具优势.目前,关于稀疏矩阵向量乘的优化在CUDA上已有一些研究成果,但在Xeon Phi上的算法优化还处于初期探索阶段,因此,文中所得实验数据和研究成果对科研和工程实践都将有所裨益. 目前的工作只是在单GPU和单Xeon Phi上进行,未来拟将优化算法移植到多GPU和MIC上,充分挖掘CPU与GPU、MIC的协同计算能力,通过实验归纳出适于两者异步计算的策略.另外,文中算法在MIC上的优化效果并不如在GPU上显著,其并行计算潜力还有待继续挖掘,今后将进一步寻找、优化适宜于在MIC上并行的算法.后续研究中,还可以针对逻辑复杂、并行度高的算法进行优化,并与GPU上的优化进行对比、总结;同时,还可针对解决稀疏线性系统的其他算法进行优化,形成解决这一类问题的计算策略、规则和模式.在Xeon Phi上求解文中问题的做法是来回通信,在后续研究中,将考虑将算法全部在Xeon Phi上求解,以达到更好的优化效果. [1] Mielikainen Jarno,Huang Bormin,Huang Allen Hung-Lung,et al.Improved GPU/CUDA based parallel weather and research forecast(WRF)simple moment 5-class(WSM5)cloud Xeon phirophysic [J].IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2012,5(4):1256- 1265. [2] 方维,孙广中,吴超,等.一种三维快速傅里叶变换并行算法 [J].计算机研究与发展,2011,48(3):440- 446. Fang Wei,Sun Guangzhong,Wu Chao,et al.A parallel algorithm of three-dimensional fast Fourier transform [J].Journal of Computer Research and Development,2011,48(3):440- 446. [3] 蔡勇,李光耀,王琥.GPU通用计算平台上中心差分格式显式有限元并行计算 [J].计算机研究与发展,2013,50(2):412- 419. Cai Yong,Li Guangyao,Wang Hu.Parallel computing of central difference explicit finite element based on GPU general computing platform [J].Journal of Computer Research and Development,2013,50(2):412- 419. [4] 唐亮,骆祖茔,赵国兴,等.利于GPU计算具有线性并行度的P/G网SOR求解算法 [J].计算机研究与发展,2013,50(7):1491- 1500. Tang Liang,Luo Zuying,Zhao Guoxing,et al.SOR-based P/G solving algorithm of linear parallelism for GPU computing [J].Journal of Computer Research and Development,2013,50(7):1491- 1500. [5] Cheng W C,Liu C H.Large-eddy simulation of flow and pollutant transports in and above two-dimensional idea-lized street canyons [J].Boundary-Layer Meteorol,2011,139(4):411- 437. [6] Liu C H,Barth M C.Large-eddy simulation of flow and scalar transport in a modeled street canyon [J].Journal of Appl Meteor,2002,41(5):660- 673. [7] Maringanti A,Athavale V,Patkar S.Acceleration of conjugate gradient method for circuit simulation using CUDA [C]∥Proceedings of HiPC 2009.Kochi:IEEE,2009:438- 444. [8] Matam K K,Kothapalli K.Accelerating sparse matrix vector multiplication in iterative methods using GPU [C]∥Proceedings of 2011 International Conference on Parallel Processing.Taipei:ACM,2011:612- 621. [9] Li Xiangge.Preconditioned conjugate gradient solver for structural problems [D].Columbia:Department of Computer Science,University of Missouri-Columbia,2013. [10] Naumov M.Parallel solution of sparse triangular linear systems in the preconditioned iterative methods on the GPU,NVR-2011- 001 [R].Santa Clara:NVIDIA,2011. [11] Reguly István,Giles Mike.Efficient sparse matrix-vector multiplication on cache-based GPUs [C]∥Proceedings of Innovative Parallel Computing.San Jose:IEEE,2012. [12] Dziekonski A,Lamecki A,Mrozowski M.A memory efficient and fast sparse matrix vector product on a GPU [J].Progress in Electromagnetics Research,2011,116(1):49- 63. [13] El Zein A,HRendell A P.Generating optimal CUDA sparse matrix-vector product implementations for evolving GPU hardware [J].Concurrency and Computation:Practice and Experience,2012,24(1):3- 13. [14] Monakov Alexander,Lokhmotov Anton,Avetisyan Arutyun.Automatically tuning sparse matrix-vector multiplication for GPU architectures [J].Lecture Notes in Computer Science,2010,59(52):111- 125. [15] 张建飞,沈德飞.基于GPU的稀疏线性系统的预条件共轭梯度法 [J].计算机应用,2013,33(3):825- 829. Zhang Jianfie,Shen Defei.GPU-based preconditioned conjugate gradient method for solving sparse linear systems [J].Journal of Computer Applications,2013,33(3):825- 829. [16] NVIDIA.Fermi compute architecture whitepaper [R].Santa Clara:NVIDIA,2009. [17] NVIDIA.CUSPARSE library [Z].Santa Clara:NVIDIA,2011. [18] 袁娥,张云泉,刘芳芳,等.SpMV的自动性能优化实现技术及其应用研究 [J].计算机研究与发展,2009,46(7):1117- 1126. Yuan E,Zhang Yunquan,Liu Fangfang,et al.Automatic performance tuning of sparse matrix-vector multiplication:implementation techniques and its application research [J].Journal of Computer Research and Development,2009,46(7):1117- 1126. [19] Bell N,Garland M.Efficient sparse matrix-vector multiplication on CUDA [R].Santa Clara:NVIDIA,2008. [20] Yuan Liang,Zhang Yunquan,Sun Xiangzheng,et al.Optimizing sparse matrix vector multiplication using diagonal storage matrix format [C]∥Proceedings of the 12th IEEE International Conference on High Performance Computing and Communications.Cidade de Goa:IEEE,2010:585- 590. [21] 孙相征,张云泉,王婷,等.对角稀疏矩阵的SpMV自适应性能优化 [J].计算机研究与发展,2013,50(3):648- 656. Sun Xiangzheng,Zhang Yunquan,Wang Ting,et al.Optimizing auto-tuning of SpMV for diagonal sparse matrices [J].Journal of Computer Research and Development,2013,50(3):648- 656. [22] Vazquez F,Ortega G,Fernandez J J,et al.Improving the performance of the sparse matrix vector product with GPUs [C]∥Proceedings of the 10th IEEE International Conference on Computer and Information Technology(CIT 2010).Bradford:IEEE,2010:1146- 1151. [23] 刘杰,刘兴平,迟利华,等.一种改进的适合并行计算的共轭剩余算法 [J].计算机学报,2006,29(3):495- 499. Liu Jie,Liu Xing-ping,Chi Li-hua,et al.An improved conjugate residual algorithm for large symmetric linear systems [J].Chinese Journal of Computer,2006,29(3):495- 499. [24] 白洪涛,欧阳丹彤,李熙铭,等.基于GPU的稀疏矩阵向量乘优化 [J].计算机科学,2010,37(8):168- 181. Bai Hong-tao,Ouyang Dan-tong,Li Xi-ming,et al.Optimizing sparse matrix-vector multiplication based on GPU [J].Computer Science,2010,37(8):168- 181. [25] 白洪涛.基于GPU的高性能并行算法研究 [D].长春:吉林大学计算机科学与技术学院,2010. [26] 吴洋,赵永华,纪国良.一类大规模稀疏矩阵特征问题求解的并行算法 [J].数值计算与计算机应用2013,34(2):137- 146. Wu Yang,Zhao Yonghua,Ji Guoliang.Parallel solving large-scale sparse matrix eigenvalue problem [J].Journal on Numerical Methods and Computer Applications,2013,34(2):137- 146. [27] 王迎瑞,任江勇,田荣.基于GPU的高性能稀疏矩阵向量乘及CG求解器优化 [J].计算机科学,2013,40(3):46- 49. Wang Ying-rui,Ren Jiang-yong,Tian Rong.Efficient sparse matrix-vector multiplication and CG solver optimization on GPU [J].Computer Science,2013,40(3):46- 49. [28] 李佳佳,张秀霞,谭光明,等.选择稀疏矩阵乘法最优存储格式的研究 [J].计算机研究与发展,2014,51(4):882- 894. Li Jiajia,Zhang Xiuxia,Tan Guangming,et al.Study of choosing the optimal storage format of sparse matrix vector multiplication [J].Journal of Computer Research and Development,2014,51(4):882- 894. [29] 赵加强.基于OpenCL的稀疏矩阵向量乘优化 [D].长春:吉林大学软件学院,2012. [30] Li Ruipeng,Saad Yousef.GPU-accelerated preconditioned iterative linear solvers [J].The Journal of Supercom-puting,2013,63(2):443- 466. [31] Larry Meadows.Experiments with WRF on Intel®many integrated core(Intel MIC)architecture [C]∥Proceedings of the IWOMP 2012.Rome:Springer-Verlag Berlin Heidelberg,2012:130- 139. [32] Intel.Intel Xeon Phi software architecture KNC technical bootcamp [EB/OL].(2014- 03- 15)[2015- 02- 03].http:∥www.intel.cn/content/www/cn/zh/processors/xeon/xeon-phi-coprocessor-system-software-developers-guide.html. [33] 英特尔亚太研发有限公司,北京并行科技公司.释放多核潜能:英特尔Parallel Studio并行开发指南 [M].北京:清华大学出版社,2010. [34] Liu X,Smelyanskiy M,Chow E,et al.Efficient sparse matrix-vector multiplication on x86-based many-core processors [C]∥Proceedings of the 27th International Conference on Supercomputing(ICS).Eugene:Association for Computing Machinery,2013:4996- 5013. [35] Liu X,Patel A,Chow E.A new scalable parallel algorithm for Fock matrix construction [C]∥Proceedings of the 28th IEEE International Parallel and Distributed Processing Symposium(IPDPS).Phoenix:IEEE,2014:902- 914. [36] Davis T A,Hu Y.The university of Florida sparse matrix collection [J].ACM Trans on Mathematical Software,2011,38(1):1- 25. Parallel Optimization and Comparison of Conjugate Gradient Method on GPU and Xeon Phi Coprocessors HuangMin1DingPing1,2LuoHai-biao2 (1.School of Software Engineering,South China University of Technology,Guangzhou 510006,Guangdong,China;2.Research Center of Parallel Software Research Center,Institute of Software Application Technology,Guangzhou & CAS,Guangzhou 511458,Guangdong,China) In order to harness the strong horsepower of multi-core processors and meet the demand of high paralle-lism,a new parallel conjugate gradient algorithm is proposed,which focuses on solving the linear equations of large-scale sparse matrices.For the GPU coprocessors,the memory hierarchy of GPU is effectively utilized,optimization methods,such as thread and matrix mappings,data merging and data multiplexing,are adopted,and an effective thread scheduling is conducted to hide the high latency of accessing the global memory of GPU.For Xeon Phi processors,the computation of high parallelism is effectively utilized to optimize data communication and transmission,data dependence reduction,vectorization and asynchronous computation,and effective thread scheduling is also conducted to hide the high latency of accessing global memory of GPU.Finally,the proposed algorithm is proved to be feasible and correct by tests on GPU and Xeon Phi,and its parallel efficiencies in two different ways are compared.It is found that the proposed algorithm on GPU has a better acceleration effect than itself on Xeon Phi. conjugate gradient method;graphics processing unit;Xeon Phi;parallel optimization;sparse matrix-vector multiplication 2015- 03- 10 广东省公益研究与能力建设专项(2014A040401018);广东省促进科技服务业发展计划项目(2013B040404009);广东省新媒体与品牌传播创新应用重点实验室资助项目(2013WSYS0002) 黄敏(1976-),女,博士,副教授,主要从事并行计算和移动云计算研究.E-mail: minh@scut.edu.cn 1000- 565X(2015)11- 0035- 12 TP391.9 10.3969/j.issn.1000-565X.2015.11.006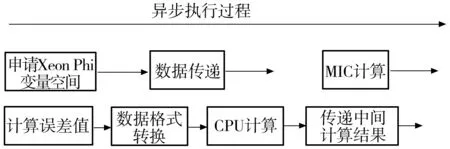
2 实验分析与总结





3 结语

