基于变载荷间隔的MSD结构疲劳可靠性研究*
薛小锋 郑香伟 冯蕴雯 冯元生
(1.西北工业大学 航空学院, 中国 西安 710072; 2.中国航空工业集团公司 第一飞机设计研究院, 陕西 西安 710089)
基于变载荷间隔的MSD结构疲劳可靠性研究*
薛小锋1郑香伟2冯蕴雯1冯元生1
(1.西北工业大学 航空学院, 中国 西安 710072; 2.中国航空工业集团公司 第一飞机设计研究院, 陕西 西安 710089)
多部位损伤(MSD)会使结构的强度大幅降低,为了防止由此造成的灾难性破坏,必须对MSD结构在整个寿命周期内的裂纹扩展情况及可靠性水平进行准确评估.文中在假设MSD结构断裂韧性和应力强度因子服从对数正态分布的基础上,结合应力强度干涉模型和二阶窄边界理论,建立了MSD结构的裂纹扩展可靠性模型;考虑MSD结构多裂纹扩展过程中的两类影响因素,推导了疲劳载荷作用下的裂纹扩展增量递推公式;结合变载荷间隔分段处理方法,提出了MSD结构随载荷循环次数变化的失效概率计算方法.通过对一受远场均匀载荷作用的含共线孔边裂纹的MSD壁板结构的分析计算,得到了MSD壁板结构失效概率随疲劳载荷作用次数的变化趋势,并将其与试验值进行比较,较为准确地反映了MSD壁板的失效趋势.
多部位损伤;裂纹扩展;可靠性;应力强度因子;概率
飞行器结构经常会出现一些由多裂纹造成的多部位损伤(MSD),其中的多裂纹扩展、连通会使结构强度大幅降低[1- 2],造成低应力水平下结构的突然破坏[3- 4],引发安全事故.工程中为了实时了解结构的安全水平及制定合理的检修周期,必须对MSD结构在其整个寿命周期内的裂纹扩展情况及可靠性水平进行准确的评估[5- 6].MSD结构在疲劳载荷作用过程中的可靠性计算主要有两方面的困难[7- 8]:一是MSD结构中多裂纹的发生和扩展机理很复杂,导致很难准确得到单次载荷作用下MSD结构的失效概率;二是在整个疲劳寿命期内逐步求解每个载荷循环下MSD结构失效概率的计算量颇为巨大.对于确定性裂纹扩展问题,目前常采用的方法是将应力强度因子求解组合模型、断裂准则以及多裂纹扩展中的相互影响处理方法(载荷循环分间隔法)综合在一起,来完成疲劳裂纹扩展分析[9- 12];而在裂纹结构疲劳可靠性方面,主要还是针对单裂纹结构来进行分析[13].不同于单裂纹结构,多裂纹相互影响的特性使得按照单裂纹分析方法得到的结果偏于危险[14],但目前鲜见针对MSD结构的考虑裂纹间相互影响的疲劳可靠性分析[15].
文中以MSD结构的疲劳多裂纹扩展寿命为研究对象,将其视为随机变量,建立MSD结构的疲劳可靠性模型;针对前述两方面困难,首先采用结构系统可靠性理论结合二阶窄边界法计算某一载荷循环下的MSD结构失效概率,然后通过裂纹综合构型系数来考虑循环载荷间隔内多裂纹扩展的相互影响,并采用变间隔分段方法来处理大量循环载荷间隔带来的计算量,在此基础上形成一种新的MSD结构疲劳可靠性分析方法.
1 MSD结构的疲劳可靠性分析
1.1 疲劳可靠性模型的建立
随着疲劳循环载荷作用次数的增加,MSD结构的可靠性出现逐渐降低的趋势,量化该降低趋势对于实时了解结构的安全水平和制定维修计划有着重要的意义.对于图1所示的含有s条裂纹的结构,其破坏是在疲劳载荷作用下由s条裂纹中最大应力强度因子超过材料的断裂韧性引起相应的裂纹失稳扩展所造成的.每条裂纹失稳扩展的概率可通过建立应力强度因子与断裂韧性的干涉模型计算得到.当疲劳载荷作用下的裂纹处于稳态疲劳扩展时,结构中的裂纹扩展量应采用相应材料的裂纹扩展速率曲线及公式进行计算.
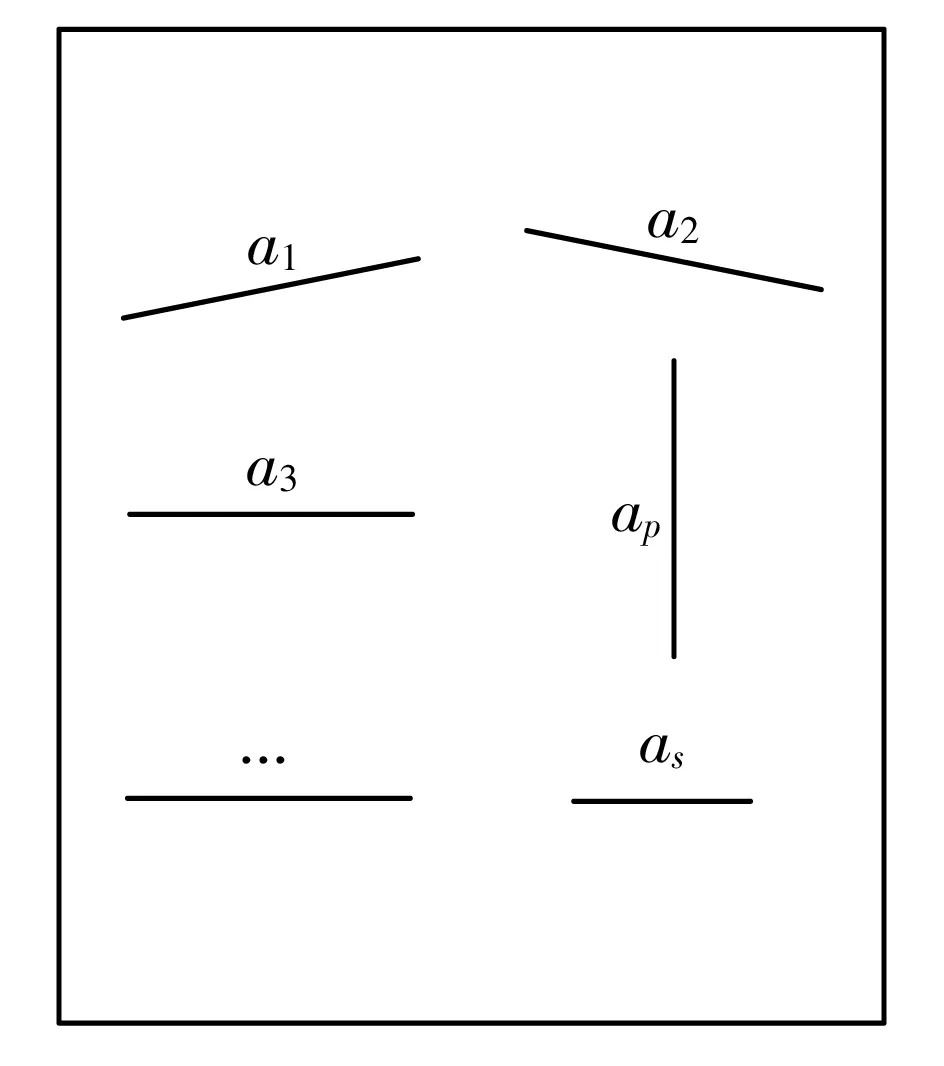
图1 有s条裂纹的MSD结构
MSD结构的疲劳可靠性模型用来研究疲劳载荷作用过程中每次疲劳载荷作用下由多裂纹扩展导致的结构失效概率.假设MSD结构的疲劳寿命为n次,则在第i次疲劳载荷作用下,对于MSD结构中的第p条裂纹,以I型裂纹为例,发生裂纹扩展的安全边界方程可以表示为
(1)


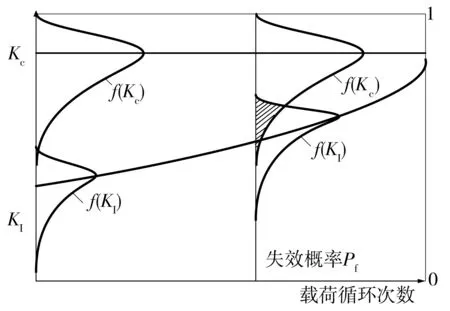
图2 应力强度因子干涉模型

(2)

(3)
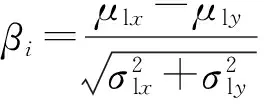
结构在受载状态下,每条裂纹失稳扩展的失效概率可由上述干涉模型计算得到.按照结构系统可靠性理论,此时结构在任意第i次疲劳载荷作用下的失效概率为
(4)
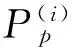
1.2 二阶窄边界法


(5)
该模型只是针对MSD结构受疲劳载荷作用下的一个状态进行可靠性分析,如果要应用到MSD结构的整个疲劳寿命分析,还需要考虑多裂纹的相互影响,计算得到每次疲劳载荷间隔内各裂纹的扩展长度,然后按照新的裂纹长度计算其应力强度因子及对应的失效概率,最终得到MSD结构的疲劳失效概率曲线.下面将通过变载荷间隔分析方法来计算MSD结构中的裂纹扩展过程,然后进行可靠性分析和计算.
2 基于变载荷间隔方法的MSD结构疲劳寿命计算
2.1 多裂纹扩展量的计算
由Paris公式[16]可知,在第i次疲劳载荷作用下,裂纹两端的扩展量可表示为
Δli=c(ΔKi)m
(6)

基于上述推导,可知相邻循环载荷间隔下的应力强度因子增量为ΔKi=f1if2iΔKi-1,据此可以对式(6)作进一步的简化.在某一载荷间隔ΔN内,裂纹在第i次循环载荷作用下的扩展量为
Δli=(f1if2i)mΔli-1,
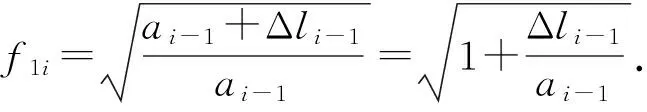

(7)

(8)
这一替代将使结果偏于保守.其中, f2i可以由近似量f2e代替[17],则有
(9)
此式可作为一个载荷间隔内f2的近似量.
综上,第n次至第n+ΔN次载荷间隔下的裂纹扩展长度可由下式计算得到:
(10)
当裂纹扩展到不同状态时,选取适当的载荷间隔,可以使上述替代对最终结果的影响变得很小.
2.2 变载荷间隔方法
MSD结构中多裂纹扩展的相互影响带来了分析上的复杂性和过大的计算量,若每一次载荷间隔都进行相互影响分析,则计算量太大.以计算结果精度和计算效率合理配置为原则,可采用变载荷间隔方法,即将结构的疲劳循环载荷进行合理分段,在每个分段中尽量用统一的参数或方法进行计算,最后将全部分段综合考虑得到最终的疲劳裂纹扩展寿命.具体方法是:计算出预先划分好的载荷间隔ΔNi中各条裂纹的扩展量,假定在ΔNi间隔内各裂纹的综合构形系数F不发生相互作用,当ΔNi次加载结束后,求出此时各裂纹相应的综合构形系数,再对下一个循环间隔ΔNi+1进行计算,直至满足最终的破坏条件.变载荷间隔分段考虑了MSD结构中多裂纹之间的相互影响,不同的载荷间隔分段对多裂纹扩展预测的精度和计算效率有很大影响,需要合理配置.对于飞行器MSD壁板结构,裂纹扩展初期的载荷间隔数可选取得稍大一些,如选取寿命的1%左右的间隔数;接近裂纹连通或破坏时则选取得稍小一些,如选取寿命的1‰左右的间隔数.
3 MSD结构疲劳可靠性分析算例
为验证文中提出的MSD结构疲劳可靠性分析方法的合理性和可行性,对一受远场均匀载荷作用的含共线孔边多裂纹的MSD试样进行了扩展寿命可靠性分析,并与试验结果进行了比较.按照不同裂纹长度,结构形式包括3种类型,如图3所示,孔边裂纹长度分别为a1、a2、a3.
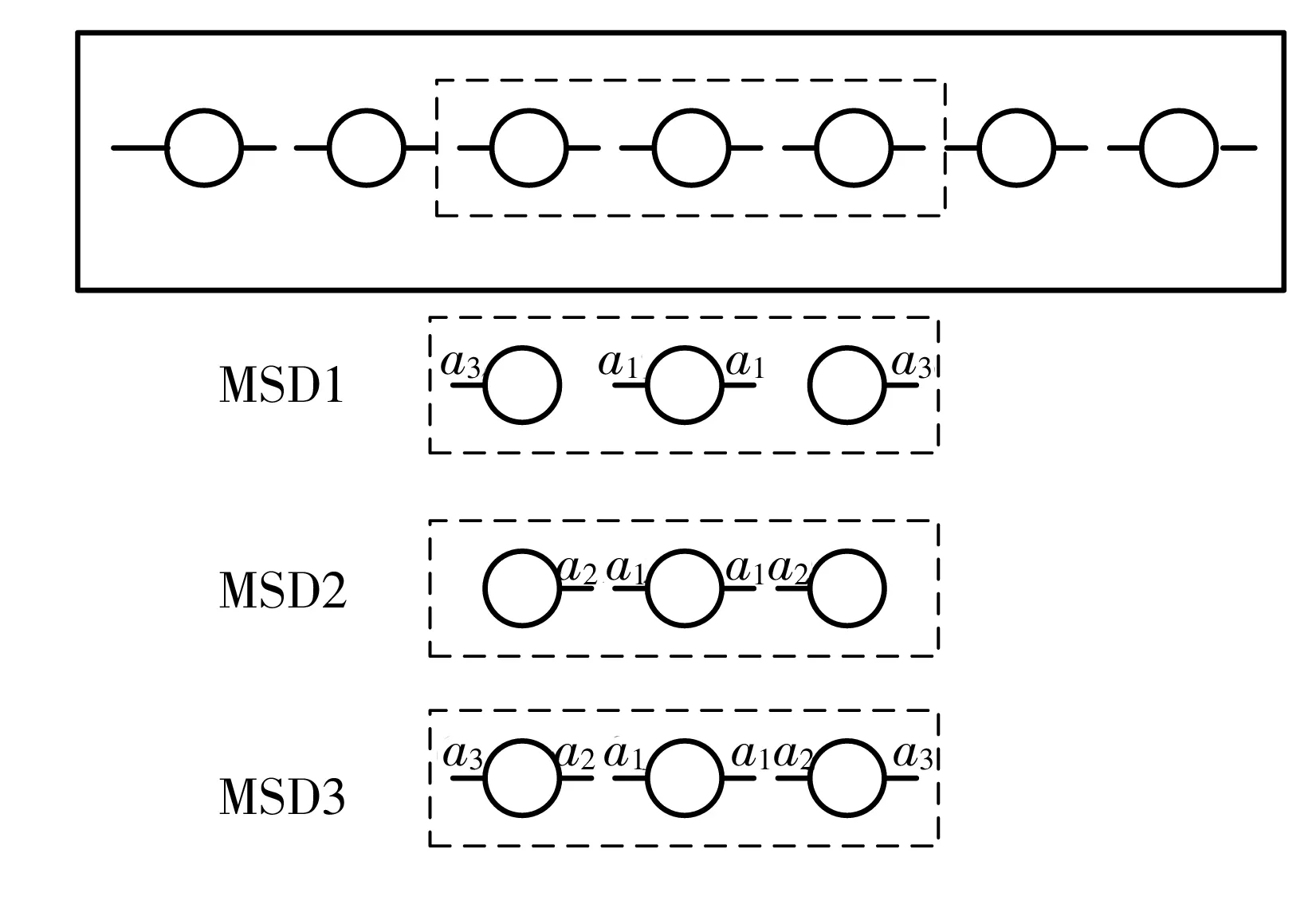
图3 MSD结构的3种裂纹形式

主要计算步骤如下:
步骤1 针对MSD结构的裂纹形式,计算第一次加载开始时各裂纹的初始参数,包括各裂纹的综合构形系数F(a0)和初始裂纹扩展量Δl0,并确定初步的变载荷间隔及对应的f2e.变载荷间隔数可按剩余韧带长度选定,韧带长度为初始长度的70%以上时变载荷间隔取为1 000,韧带长度为初始长度的40%~70%时变载荷间隔取为100,韧带长度为初始长度的40%以下时变载荷间隔取为10.
步骤2 按所提工程简化算法,计算该载荷间隔ΔN内的各裂纹扩展长度ΔaΔN,

累加到各裂纹长度后,按照步骤1继续计算下一个变载荷间隔的各裂纹扩展长度.
步骤3 当相邻裂纹连通、裂纹与邻孔连通或发生失稳扩展时,计算完成,记录所有间隔数目及每个间隔中各裂纹的扩展长度,得到该MSD结构的裂纹扩展寿命.
步骤4 计算每条裂纹在各间隔下的实际长度,根据加载情况计算各裂纹的应力强度因子,并根据文献[5]中的应力强度因子变异系数求解方法得到变异系数.
步骤5 将各裂纹的应力强度因子及其变异系数、MSD结构的断裂韧性及其变异系数代入文中所建立的疲劳可靠性模型中,求解得到MSD结构的失效概率.
表1给出了采用文中方法计算得到的各MSD结构的疲劳多裂纹扩展寿命,并将裂纹扩展寿命与试验结果进行了对比.
由表1可知,改进后算法的计算精度基本满足要求.随着疲劳载荷加载次数的增加,MSD结构的失效概率逐渐增加,4种构型的MSD结构的失效概率随循环载荷次数的变化情况如图4所示.可知,在加载的后期,失效概率增加很快,最终达到0.5,即达到MSD结构临界破坏的状态(应力强度因子等于断裂韧性的状态).由MSD1_20和MSD1_40两种多裂纹配置的疲劳可靠性计算结果可知(分别对应于图4中的曲线1和4),裂纹间的韧带越长,结构的疲劳寿命越长,载荷作用次数相同时的失效概率越小.

表1 MSD结构裂纹疲劳寿命计算值与试验值的对比1)
1)a1r、a2r、a3r分别为与裂纹扩展寿命相对应的裂纹尺寸.
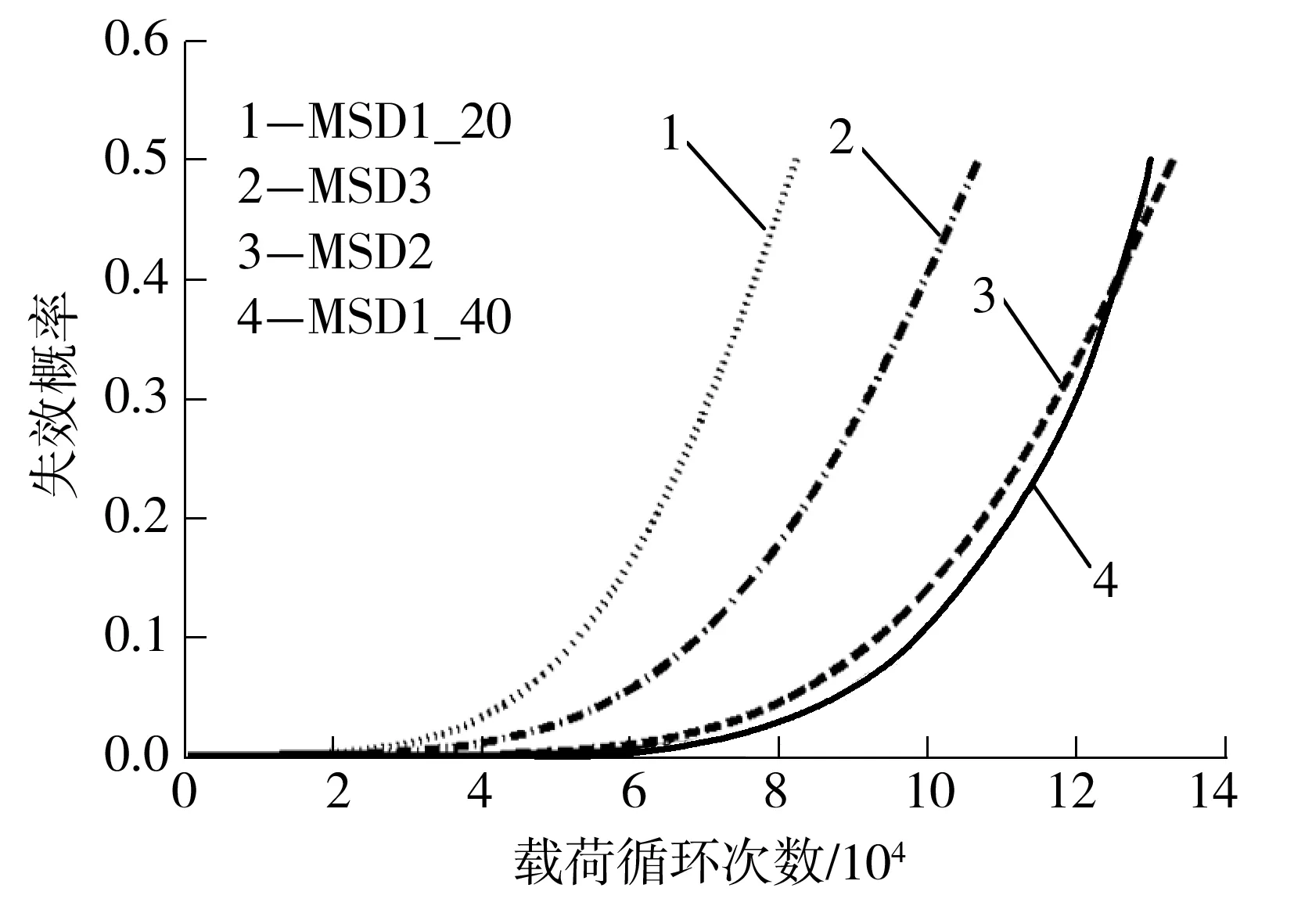
图4 MSD结构失效概率随载荷循环次数的变化
Fig.4 Failure probability of MSD structure varying with fatigue load cycle
4 结语
在裂纹疲劳扩展过程中,MSD结构的裂纹间存在着明显的相互影响,难以对其疲劳寿命及可靠性进行准确的定量分析,因此有必要采用一些数学手段来克服因多裂纹相互影响而造成的MSD结构疲劳寿命及可靠性分析困难.鉴于此,文中根据MSD结构中多裂纹的扩展特性给出了裂纹扩展过程中裂纹失稳扩展的失效概率计算公式,该式需要在各裂纹长度和随循环载荷次数之间关系明确的前提下才能使用.在考虑两类因素对裂纹扩展速度影响的前提下,推导了多裂纹扩展长度的近似算法,提出了更合理的变载荷间隔分段方法来计算孔边共线MSD结构的疲劳扩展寿命,所得最终计算值偏于保守.
采用文中方法,可最终得到MSD结构随疲劳载荷作用次数增加的失效概率变化情况,进一步可得到给定失效概率下的疲劳载荷作用次数,即一定可靠度下的MSD结构寿命,从而为MSD结构的检修周期制定提供依据.后续将针对变幅载荷作用下MSD结构的疲劳可靠性问题开展研究,使本项研究更具工程实际意义.
[1] Ooi E T,Yang Z J.A hybrid finite element-scaled boundary finite element method for crack propagation modeling [J].Computer Methods in Applied Mechanics and Engineering,2010,199(17/18/19/20):1178- 1192.
[2] Pryl Dobromil,Cervenka Jan,Pukl Radomir,et al.Mate-rial model for finite element modelling of fatigue crack growth in concrete [J].Procedia Engineering,2010,2(1):203- 212.
[3] Stanislav Seitl,Zdenek Knesl.Two parameter fracture mechanics:fatigue crack behavior under mixed mode conditions [J].Engineering Fracture Mechanics,2008,75(3):857- 865.
[4] Wu X R,Xu W.Strip yield crack analysis for multiple site damage in infinite and finite panels—a weight function approach [J].Engineering Fracture Mechanics,2011,78(14):2585- 2596.
[5] 薛小锋,冯蕴雯,冯元生.基于随机有限元法的平面多裂纹结构可靠性研究 [J].西北工业大学学报,2012,30(4):508- 511. Xue Xiao-feng,Feng Yun-wen,Feng Yuan-sheng.Exploring theoretically reliability of multiple-crack structure by applying Taylor stochastic finite element method(TSFEM) [J].Journal of Northwestern Polytechnical University,2012,30(4):508- 511.
[6] Xue X F,Feng Y W,Feng Y S.Residual strength of multiple-site damage structure on aged aircraft using interactions of Dugdale-type cracks and stable tearing [J].Advanced Materials Research,2012,487(1):539- 543.
[7] Yan X Q.Multiple crack fatigue growth modeling by displacement discontinuity method with crack-tip elements [J].Applied Mathematical Modeling,2006,30(6):489- 508.
[8] Adib A M L,Baptista C A R P.An exponential equation of fatigue crack growth in titanium [J].Materials Science and Engineering,2007,452/453:321- 325.
[9] Pidaparti R M V,Palakal M J,Rahman Z A.Simulation of structural integrity predictions for panels with multiple site damage [J].Advances in Engineering Software,2000,31(2):127- 135.
[10] Lucas F M S,Gonçalves J P M,Oliveira F M F,et al.Multiple-site damage in riveted lap-joints:experimental simulation and finite element prediction [J].International Journal of Fatigue,2000,22(4):319- 338.
[11] De Matos P F P,Nowell D.Numerical simulation of plasticity-induced fatigue crack closure with emphasis on the crack growth scheme:2D and 3D analyses [J].Engineering Fracture Mechanics,2008,75(8):2087- 2114.
[12] Labeac G,Diamantakos J,Kermanidis T.Crack link-up for multiple site damage using an energy density approach [J].Theoretical and Applied Fracture Mecha-nics,2005,43(2):233- 243.
[13] Xue Xiaofeng,Feng Yunwen,Ying Zhongwei,et al.Research of plane multiple cracks stress intensity factors based on stochastic finite element method [J].Chinese Journal of Aeronautic,2009,22(3):257- 261.
[14] Chang D,Kotousov A.A strip yield model for two colli-near cracks [J].Engineering Fracture Mechanics,2012,90(8):121- 128.
[15] Edson Denner Leonel,Wilson Sergio Venturini.Multiple random crack propagation using a boundary element formulation [J].Engineering Fracture Mechanics,2011,78(6):1077- 1090.
[16] 刘文珽.KIC实验数据的统计处理 [J].固体力学学报,1981,2(1):92- 98. Liu Wen-ting.Statistical treatment of KIC test data [J].Acta Mechanica Solida Sinica,1981,2(1):92- 98.
[17] 应中伟,冯蕴雯,薛小锋,等.改进的载荷循环分间隔法计算工程问题中MSD裂纹扩展问题的研究 [J].航空学报,2008,29(4):898- 902. Ying Zhong-wei,Feng Yun-wen,Xue Xiao-feng,et al.Improved division of cyclic loading method for MSD fatigue crack growth in engineering [J].Acta Aeronautica et Astronautica Sinica,2008,29(4):898- 902.
[18] Pártl O,Schijve J.Multiple-sit damage in 2024-T3 alloy sheet [J].International Journal of Fatigue,1993,15(4):293- 299.
Investigation into Fatigue Reliability of MSD Structure by Modifiable Division of Cyclic Loading Method
XueXiao-feng1ZhengXiang-wei2FengYun-wen1FengYuan-sheng1
(1.College of Aeronautics,Northwestern Polytechnical University,Xi’an 710072,Shaanxi,China;2.The First Aircraft Institute,Aviation Industry Corporation of China,Xi’an 710089,Shaanxi,China)
MSD (Multiple Site Damage) can cause the structure strength to degrade, which may lead to a catastrophic failure. In order to avoid the failure, the crack growth and reliability of the MSD structure in its whole life cycle should be exactly evaluated. In this paper, assuming that the fracture toughness and stress intensity factor of the MSD structure follow the lognormal distribution, a multiple-crack propagation reliability model of the MSD structure is constructed by combining the stress-strength interference model and the second boundary theory. In view of two influencing factors related to the crack growth of the MSD structure, a recursion relation of crack growth length under fatigue load is deduced. Then, by drawing on the modifiable division of the cyclic loading method, a calculation method of the failure probability of the MSD structure with changing load cycles is proposed. Finally, by analyzing and calculating a MSD panel with collinear hole-edge cracks under far-field uniform load, the variation trends of the failure probability of the MSD panel with fatigue load cycles are obtained, and the calculation results are compared with the experimental ones. It is found that the proposed method can reflect the failure trends of the MSD panel more accurately.
multiple site damage; crack growth; reliability; stress intensity factor; probability
2014- 04- 18
国家自然科学基金资助项目(10577015) Foundation item: Supported by the National Natural Science Foundation of China(10577015)
薛小锋(1982-),男,博士,讲师,主要从事飞行器结构可靠性分析与设计研究.E-mail: xuexiaofeng@mail.nwpu.edu.cn
1000- 565X(2015)11- 0145- 06
O 346.2
10.3969/j.issn.1000-565X.2015.11.020

