“一题多变”的解题教学，打开学生思维的通道

☉江苏省苏州市高新区实验初级中学 练兆明

“一题多变”的解题教学，打开学生思维的通道

☉江苏省苏州市高新区实验初级中学 练兆明

教师借助于例题进行教学，用习题衡量学生掌握知识的情况，设计形式多样的练习促使学生将知识转化为技能，这是教师教学中常用的方法.因此，重视研究习题和解题教学，是提高教学质量、巩固深化知识、发展学生思维能力和增强学生解题能力的重要途径.

波利亚说：“教学生解题是意志的教育，但学生求解那些对他来说并不太容易的题目时，他学会了败而不馁，学会了赞赏微小的进展，学会了等待灵感的到来，学会了当灵感到来后全力以赴.如果在学校里没有机会尝尽为求解而奋斗的喜怒哀乐，那么他的数学教育就在最重要的地方失败了.”

新的数学教学大纲要求教师树立学生发展的教育观念，改革教学方法和教学手段，激发学生学习数学的兴趣，培养学生的创新精神和实践能力，提高学生的素质，塑造学生创造性的人格.而现行初中数学课本中，不少习题内涵丰富，对学生思维能力的培养有着不同寻常的作用和丰富的教学价值.而我们教师在使用过程中要做到：一、精选；二、会用；三、善变.下面攫取一二，与各位老师共同探讨.

一、习题变式，发挥概念对解题的作用

在讲清概念，特别是几何图形的概念后，对题目进行简单的变式，让刚讲完的概念对解题起到举足轻重的作用.

案例1在讲完等腰梯形的概念后，可通过以下几道变式的题目进行巩固.

（1）如图1，等腰梯形的两底长分别为3cm和7cm，高为4cm，则它的腰为_________.

（2）如图2，等腰梯形的两底长分别为3cm和7cm，∠B=60°，则它的腰为_________.

（3）如图3，等腰梯形的两底长分别为3cm和7cm，AC⊥BD，则它的腰为_________.

图1

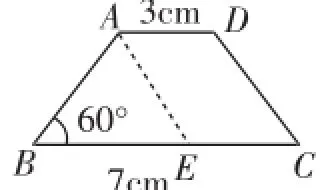
图2

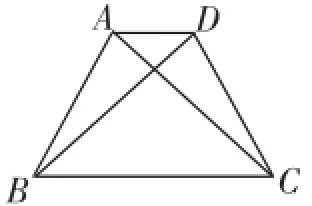
图3

二、增加解题灵活性，发展学生思维

在学生具备了一定的解题能力，或者在章节学完后进行复习巩固时，可以提供以下档次的题目.

案例2讲完“正方形”这节内容后，就可以进行以下的题目训练：如图4，四边形ABCD是正方形，点G是BC上的任意一点，DE⊥AG于点E，BF∥DE，且交AG于点F，求证：AF-BF=EF.

利用正方形的有关性质与学生最熟悉的全等三角形知识，学生相对比较容易做出该题.所以教师可以作以下的变化，让学生再思考：

在正方形ABCD中，点P是CD上一动点，连接PA，分别过点B、D作BE⊥PA、DF⊥PA，垂足为E、F，请探索BE、DF、EF这三条线段长度有怎样的数量关系？

图5是先让点P在正方形的边长CD上“运动”，学生可以模仿课本上的题目进行猜想与证明，图6与图7则让点P在正方形的边长CD的延长线上“运动”，把学生的思维引领到另一个高度.

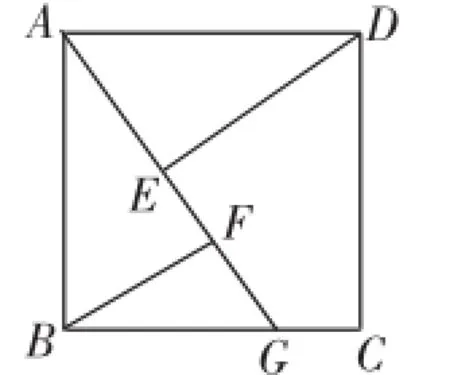
图4

图5

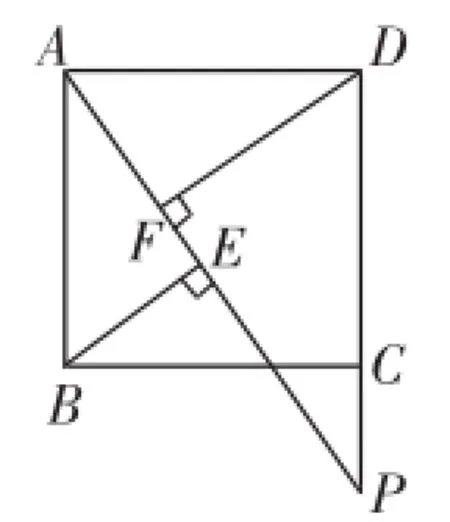
图6

图7

如图8，ABCD是一个正方形花园，E、F是它的两个门，且DE=CF，要修建两条路BE和AF，这两条路等长吗？它们有什么位置关系？

图8

利用同样的知识点学生也是相对比较容易做出该题，这两道题可以放到一起进行训练，让学生进行比较，总结相同与不同之处.也可以分开一段时间，讲新课时先做一题，留一题到复习时再用，那么就可以起到巩固提高的作用.如果是复习时再用，那么教师又可作以下的变动，让学生再思考：

已知正方形ABCD，如图9，E是AD上的一点，过BE上一点O作BE的垂线，交AB于点G，交CD于点H，求证：BE= GH.

图9是在原题上稍作变动，即把原题中的一个结论BE⊥GH作为已知，G为AB上任意一点，指导学生去作辅助线AH′∥GH（如图12），然后证明全等才能得到最后的结果.

图9

图10

图11

图10在图9的基础上又作变动，E、F、G、H四点都在正方形的边上，EF⊥GH，结论变为求证：EF=GH.指导学生去作辅助线AM∥EF，DN∥GH（如图13），然后再证明全等就可得到最后的结果.

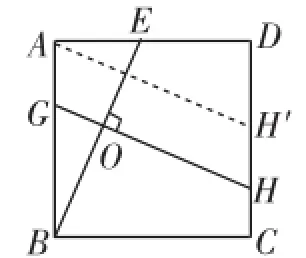
图12

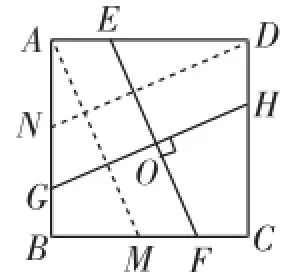
图13

图14

图11干脆把E、F、G、H四点搬到了正方形边长的延长线上，还是EF⊥GH，结论还是求证：EF=GH.指导学生根据上两题的思路，把EF、GH平移回到正方形内部（如图14），采用相同的方法可以得到相同的结论.

需要作辅助线的题目，对初中学生来说就是一个难点，甚至成了一道不易跨越的鸿沟，在教学当中教师精选课本上的习题，把这些典型的题目用好、变通，让学生从题海中跳出来，不失为老师与学生的共同福音.

解题是数学的重要教学活动，解题过程中当学生思维受阻，处于时而豁然开朗、时而陷入困境时，给予恰当的点拨，会对学生影响极深；当学生对待困难处在犹豫不决时，给予点拨与鼓励，学生会信心十足；当学生的解法有创新时，给予点拨与肯定，学生会更上一层楼……这不仅是点拨解题，也是点拨人生.

三、增加题目的难度和变化

对于有数学天赋、学有余力的学生，则可设置一些选学内容或课本习题中较难的题目加以变化，让他们的聪明智慧能得到淋漓尽致的发挥.

案例3在一副三角板中，将一块含30°角的三角板DEF的直角顶点D放在一块含45°角的三角板ABC的斜边AC的中点上逆时针方向旋转，直角三角板DEF的短直角边为DE，长直角边为DF，且AB=BC=4.

（1）如图15，在上述旋转过程中，DM与DN，BM与CN有怎样的数量关系？

（2）在上述旋转过程中，两块三角板重叠出四边形DMBN的面积是否发生变化？若变化，如何变化；若不变，求出当时四边形DMBN的面积.

（3）继续旋转至图16、图17的位置，图16延长AB、BC交DE、DF于M、N；图17延长FD、ED交BC、AB于N、M，则DM与DN，BM与CN有怎样的数量关系，请写出结论.

图15

图17

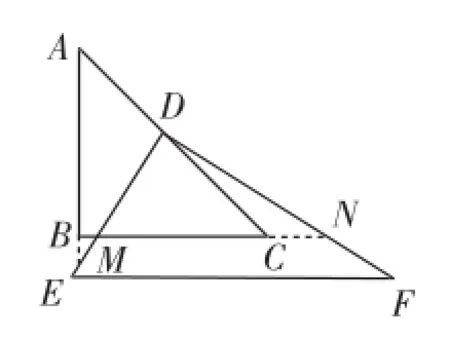
图16

还可以把图形变换成以下两个“矩形”与“三角形”，如图18，O为矩形ABCD的中心，将直角三角板的直角顶点与O点重合，转动三角板使两直角边始终与BC、AB相交，交点分别为M、N.如果AB=4，AD=6，OM=x，ON=y，则y与x的关系是_________.

总之，长期的教学实践使笔者体会到：如能对基础题加以研究，触类旁通，将收到事半功倍的效果.一题多变是开发智力、培养能力的一种行之有效的方法，进行思维分析，探讨解题规律和对习题的多角度“追踪”，能“以少胜多”地巩固基础知识，提高分析问题和解决问题的能力.掌握基本的解题方法和技巧，这对沟通不同知识之间的联系，开拓思路，培养发散思维能力，激发学生的学习兴趣都是十分有益的.

图18

1.文卫星.数学教学中的育人艺术［J］.中学数学教学参考，2003（7）.

2.肖研.关于初中数学解题教学的几点建议——让学生在“讲题”中提高数学能力［J］.课程教育研究，2013（10）.

3.平志明.培养学生良好的解题习惯优化初中数学教学［J］.数学学习与研究，2011（14）.H