点动图变思构图，特殊出发想一般——从北京两道八年级几何综合题说起

☉江苏省宜兴市树人中学 孙登高

☉江苏省无锡市金星中学 朱宸材

点动图变思构图，特殊出发想一般
——从北京两道八年级几何综合题说起

☉江苏省宜兴市树人中学 孙登高

☉江苏省无锡市金星中学 朱宸材

据笔者教学经历所见，新世纪以来的课程改革在一定程度上降低了几何教学的要求，反映在相关教材上，一方面将过去很多繁难的几何问题从教材上删减；另一方面也破坏了几何严谨的逻辑体系，对基层几何教学带来一定的干扰.然而，最近研习北京相关地区2014～2015学年第一学期八年级期末试题时，欣喜地发现，北京各个区八年级试卷的最后一道综合题竟然大多使用了几何考题，这种通过地区考卷强势引领几何教学的命题导向值得点赞！本文选取其中一些典型几何习题，讲解动点问题的证明策略，并反思几何变式中考查“特殊与一般”的关系.

一、两道八年级几何综合题及思路简述

例1（北京市东城区（南区）2014～2015学年第一学期八年级卷）在等边△ABC中，点E在AB上，点D在CB的延长线上，且ED=EC.

（1）若点E是AB的中点，如图1，求证：AE=DB.

（2）若点E不是AB的中点时，如图2，试确定线段AE与DB的大小关系，并写出证明过程.

图1

图2

思路简述：（1）容易证出等腰△BDE，从而有BD=BE.又点E是AB的中点，获证AE=DB.

（2）如图3，过点E作EF∥BC交AC于点F.由△ABC是等边三角形，得∠ABC=∠ACB=∠A=60°，AB= AC=BC，由EF∥BC，得∠AEF=∠ABC=60°，∠AFE=∠ACB=60°，即∠AEF=∠AFE=∠A=60°，所以△AEF是等边三角形.于是∠DBE=∠EFC=120°，∠D+∠BED=∠FCE+∠ECD=60°，再结合DE=EC，得∠D=∠ECD，∠BED=∠ECF.于是可证△DEB≌△ECF.得BD= EF=AE，即AE=BD.

图3

例2（北京市朝阳区2014～2015学年第一学期八年级卷）在△ABC中，∠BAC=90°，AB=AC，作∠ACM，使得点D是直线BC上的动点，过点D作直线CM的垂线，垂足为E，交直线AC于点F.

（1）当点D与点B重合时，如图4所示，DF与EC的数量关系是________；

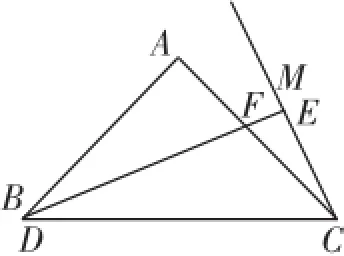
图4

（2）当点D在直线BC上运动时，DF和EC是否始终保持上述数量关系呢？请你画出点D运动到CB延长线上某一点时的图形，并证明此时DF与EC的数量关系.

思路简述：（1）结合题意知道在Rt△ABF和Rt△CEF中，有一组对顶角相等，从而由等角的余角相等得∠ABF=∠ACM，结合∠ABC可代换出∠ABF=，即此时BE平分∠ABC！想清楚这点后，就容易构造出如图5的辅助线，延长BA交CM于G点，易证得△BGE≌△BCE，从而有GE=CE；另外又可证得△ABF≌△ACG，从而有BF=CG；于是BF=2CE，问题获解.

（2）根据要求先构造图6，受到（1）中思路的启发，过点D作DH⊥CA，并交CM于点G，容易得到等腰Rt△CDH，证得△DGE≌△DCE，从而有GE=CE；另外又可证得△HDF≌△HCG，从而有DF=CG；于是DF=2CE，问题获解.

图5

图6

二、关于教学导向的思考

事实上，不仅是上述两个地区在全卷最后一题安排了几何题的变式考查，就笔者检索所见，北京海淀区、昌平区、西城区等地最后一题也都不约而同地选择了几何题的变式综合题.那么，这类考题的教学导向何在呢？以下围绕几何解题教学、变式教学阐释一些个性化的认识.

1.几何解题教学，努力追求一题多变

我们知道教材上新授课期间的例习题常常是为了巩固训练图形的性质或判定定理，功能较为单一，缺少对问题本身的深入追问，像上文摘引的两道考题，则对一个问题进行了一题多变，追求了从特殊到一般的解题思想.同时，值得一说的是，就几何解题教学来说，不仅要追求一题多变，将问题从特殊引向一般，训练思维的深刻性、求变性；还要注意一题多解的训练，训练同一问题的多样化求解；进一步，在对一题多解的点评环节，还需要引导学生对一题多解作出必要的反思，即为什么问题会有这么多的解法？这些不同解法的背后又有怎样的相同点？多思考这些问题常常能让我们走向问题的深度，解题教学自然也能追求一定的教学深度.

2.倡导变式教学，启发学生学会思考

我们知道，经由顾泠沅教授等人的努力，变式教学已成为我国数学教育的重要特色，其研究范围不仅在解题教学中大力开展变式教学，包括概念在内的变式教学研究也已十分深入，值得广大一线教师关注.就本文所引摘的两道几何变式考题来看，解题教学中倡导变式教学就需要思考“从特殊走向一般”的变式取向，而这也是把思维定势引向求变思维，如例2中，当点D在直线BC上运动时，需要分三种不同的位置关系（点在CB延长线上、在线段CB上、在BC延长线上）研究，而证明的思路又是一致的，都是要构造等腰三角形再证全等.容易看出，认真开展这样的变式教学，长期坚持，学生收获的并不仅仅是解题能力的提升，而是启发他们学会思考、学会探索未知领域，在一定意义上，也就追求了郑毓信教授所倡导的“从开放题到开放式教学”.

三、实践跟进

坐而论道，不如起而行之.以下就以教材上的习题为例，变式设问，追求解题教学效益的更大化.

例3（人教七下第20页，练习2）如图7，△ABC中，D是AB上一点，E是AC上一点，∠ADE=60°，∠B= 60°，∠AED=40°.

图7

（1）图中还能求出哪些角的度数？直接写出.

（2）用两种思路证明DE∥BC.

（3）连接BE，当EB恰好平分∠ABC时，△BDE是等腰三角形吗？说明理由.

（4）过点A作△ABC的高AH，求证：AH⊥DE.

变式意图：通过前两问有效巩固训练了新学内容（平行线的性质与判定），接着又通过系列变式，引导学生积累基本图形（当“平行”遇上“平分”会形成等腰三角形），而最后一问引导学生积累“如果一条直线垂直于平行线中的一条直线，则它也垂直于另一条直线.”

例4（人教七下第22页，第2题）如图8，在四边形ABCD中，如果AD∥BC，∠B=60°.

（1）能直接求出哪个角的度数？写出推理语句.

（2）请再添加一个条件，求出这个四边形的所有内角的角度.

（3）作∠ABC的平分线交AD于点E，再作∠BCD的平分线交BE于点H，若BE⊥CH时，求证AB∥CD.

变式意图：前两问训练平行线的性质，后一问启发学生积累基本图形所对应的命题“两直线平行，同旁内角的平分线互相垂直”，并思辨该命题的逆命题.因为就变式问题来看，将原命题变式为逆命题是常见的变式取向和思考方向，要启发学生多思考这样的问题，几何中很多定理都具有互逆定理，如勾股定理与逆定理、平行线的性质与判定、平行四边形的性质与判定等.

图8

四、写在最后

本文关注的、列举的都是几何教学中的题例，事实上，解题教学中到处都可见变式存在，需要教师本身对问题的呈现方式、解法多样化、问题可能的生长方向有着较好的理解，在这个意义上说，理解数学、理解解题，首先要从我们做起，所谓解题教学功夫在于课堂之外，也就是这个道理吧.

1.章建跃.发挥数学的内在力量，为学生谋取长期利益［J］.数学通报，2013（2）.

2.史宁中，主编.基本概念与运算法则——小学数学教学中的核心问题［M］.北京：高等教育出版社，2013.

3.夏盛亮.引导回归教材，倡导开放取向——一次县级期末卷的命题取向分析［J］.中学数学（下），2014（1）.

4.郑毓信.开放题与开放式教学［J］.中学数学教学参考，2001（3）.H