“同位角相等，两直线平行”三段引入内容分析

☉江苏省宿迁市宿豫区教育局教研室 胡 滨

“同位角相等，两直线平行”三段引入内容分析

☉江苏省宿迁市宿豫区教育局教研室 胡 滨

“探索直线平行的条件”的第1课时，是介绍“同位角相等，两直线平行”的几何基本事实，不同版本的新课程教材有不同的呈现方式，以下三段引入内容被多种教材所呈现：用“木工用角尺在工件上画平行线”作为情境引入、用“用三角尺与直尺画平行线”作为画图引入、用“用三根小棒直观演示”作为操作引入.这样三段内容在实际课堂教学引入中可行吗？又何以可能？我们对这三段内容的呈现方式分析如下，供大家参考.

一、用“木工用角尺在工件上画平行线”作为情境引入的分析

木工用的“角尺”拐角之所以设计成直角，源于对垂直的理解.如图1，假设一根绳子的端点处固定一重物，使得重物自然下垂，那么这条绳子就与地平面垂直.因此垂直中的“垂”是下垂的意思，“直”是相对于“倾斜”而言的，也就是“不斜”的意思.

由于“角尺”的两边互相垂直，当一边与工件密合时，沿着另一边所画出来的线自然互相平行，如图2中a∥b.这样的事实，我们直观观察时似乎本性自明，当反省其中的道理时却又不知所云，特别是当要求用语言来概括其中的道理时，更是难以形容尽致.

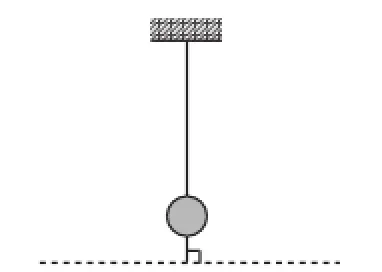
图1

图2

实际上，物各有性，性各有理.图2中a∥b的事实，说明我们关于平行线的知识来源于感官所得，“平行”的效果是由实验知道的.原因先于效果，原因是不可实验的，它隐藏于事物之中，物有形，理却无形，但理是实理.怎样才能发现图2中a∥b的“实理”呢？“理”就在图2中具有相同位置关系的∠1与∠2都为90°这一“因”.这个隐藏在“角尺”的拐角处的事实可能被工具直观所遮蔽而视而不“见”，也可能是由于“直角”的“直”之理太平常而无法“言”表.

用“木工用角尺在工件上画平行线”作为情境引入，既符合人的先从觉识意象感知、后理性推理验证的认识规律，又符合因果相似、有果必有因的因果相随的自然规律.为此，选择这个情境引入是可行的.

二、用“用三角尺与直尺画平行线”作为画图引入的分析

平行线的研究对象是直线，“直的线”含义是“它上面的点一样地平放着的线”［1］，“点一样地平放着”指在直线上任意截取一条线段，就会出现两个端点，这两个端点之间的线段上所有点都不会偏离到上方或下方.这就是说，“直线”之所以“直”，是因为它上面任意一条线段的方向都与原直线的方向一样.因此，“直线”中的“直”的含义指有确定的方向.

“平行线”的意义指“在同一平面内的直线，向两个方向无限延长，在不论哪个方向它们都不相交”［1］，两条直线“不相交”指它们的方向相同且无论在哪个方向上都不会构成角.因此，“平行线”中的“平行”的含义指有相同的方向.

当线上的点的方向有所改变时，线就会变“曲”，如图3；当直线上某一段的方向有所改变时，就会变“倾斜”，如图4；当同一平面内的两条直线的方向不相同时，就会相交而构成角，如图5.因此，“直”与“曲”相对，“直”也与“斜”相对.线的“曲”与“斜”均与“角”有关，“角是在一平面内但不在一条直线上的两条相交线相互的倾斜度”［1］.因此，描述平行线的特征必用到角，对角的认识又以直线为基础.

图3

图4

图5

如图6［2］，用三角尺与直尺来推画平行线，既能确定直线的方向又能保持直线的方向相同，这样的确定必以同位角的恒定为基础.因此，用“用三角尺与直尺画平行线”作为探索直线的平行条件过程中的画图技能培养是重要的.

图6

三、用“用三根小棒直观演示”作为操作引入的分析

如图7，三根木条相交成∠1、∠2，固定木条b、c，转动木条a.

图7

如图8（1），在木条a的转动过程中，观察∠2的变化以及它与∠1的大小关系，你发现木条a与木条b的位置关系发生了什么变化？木条a何时与木条b平行？

改变图7中∠1的大小，按照上面的方式再做一做.∠1与∠2的大小满足什么关系时，木条a与木条b平行？与同伴进行交流［3］.

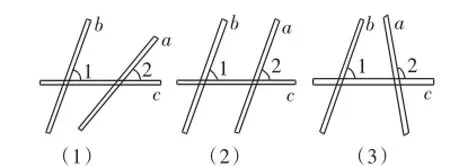
图8

简化木条图，得到图9.可以看出，画直线AB的平行线CD，实际上就是过点P画与∠2相等的∠1，而∠2和∠1正是直线AB、CD被直线EF截得的同位角.这说明：如果同位角相等，那么AB∥CD［4］.

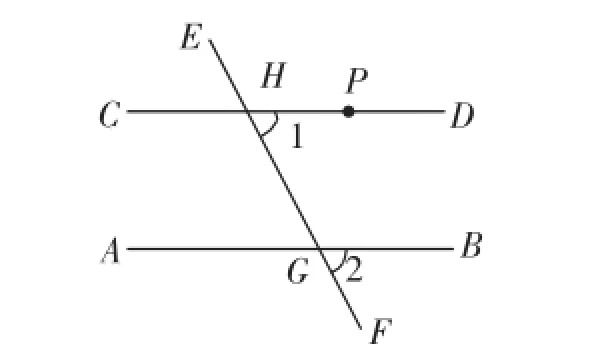
图9

从图7、8的“三根小木棒”抽象到图9中的“三线八角”，抽去了木棒这一物质条件，抽取了“两条直线AB、CD被第三条直线EF所截，如果∠1=∠2，那么AB∥CD”这一基本事实.抽象的关键是洞见“用三根小木棒直观演示”中的物性物理，认识到抽象图形中固有的平行原理.抽象过程带来的启示是：数学实验的直观操作只是知识的开端，而数学思想方法的获得主要还需仰借个人理性分析与推证，思外物，懂外物，使思想通达外物的真性实理.因此，用“用三根小棒直观演示”作为探索直线的平行条件的操作是不可缺少的.

由此看来，三段内容之间遵循前后相继的秩序，先由观察物体而获得感官知觉力，后由观察图形而获得想象力（包括动手操作能力），最后洞见到抽象的平行原理而获得智力上的领悟.也就是先由物体的本性本理，后到几何的图形形理，最后抽象为基本的事实原理.缺乏了物体现实可见之本性本理，眼睛的视界便会视而不见；缺乏了基本作图几何直观之图形形理，对数学本原的理解及推理能力的培养便会落空；缺乏了从实物演示抽象到规范的几何之事实原理，会影响对数学对象本质的准确地把握及数学模型建立过程的清晰认识.

为此，命题“同位角相等，两直线平行”获得过程的教学设计，要关注两种方式［5］.首先应关注它的形成.木工用“角尺”在工件上画平行线，说明平行线有特例形式；在平面上，我们用三角尺和直尺画平行线，说明平行线普遍存在；从“三根小木棒”到“三线八角”的形成过程，说明平行线条件的原理过程是可抽象、可概括、可归纳的.在这三个阶段中，有辨认、假设、验证、抽象、概括等一系列认知加工过程，是一种发现的学习过程.其次应关注它的同化形式.平行线的条件与直线、角、平行等概念都有关系，角的概念与直线及其方向密切相关，直线与方向及其方向的改变有关内容又都与角相关联，它们分布在“图形与几何”领域的各个方面，如何将这些相关的内容激活、联结，并经过加工和改组，以形成新的平行线认知结构，是一种有意义的接受学习过程.在实际的教学设计过程中，既要关注命题形成的发现过程，又要关注命题意义的接受过程，也只有兼顾这两个过程，理解、阐释与使用这三段引入内容才是可行且可能的.

1.欧几里得，著.几何原本［M］.兰纪正，朱恩宽，译.西安：陕西科学技术出版社，1990.

2.中华人民共和国教育部审定.义务教育教科书七年级数学（下册）［M］.南京：江苏科学技术出版社，2013.

3.中华人民共和国教育部审定.义务教育教科书七年级数学（下册）［M］.北京：北京师范大学出版社，2013.

4.中华人民共和国教育部审定.义务教育教科书七年级数学（下册）［M］.北京：人民教育出版社，2013.

5.俞平.数学教学心理学［M］.北京：北京师范大学出版社，2010.Z