单元教学：整体构思效率高——以“平行线的性质”教学设计为例

☉江苏省南京市莲花实验学校 吉明华

单元教学：整体构思效率高
——以“平行线的性质”教学设计为例

☉江苏省南京市莲花实验学校 吉明华

近读《中学数学》，章志霞老师在《基于“整体观”的几何教学与反思——以“平行线的判定”教学为例》一文中对“平行线的判定”给出了整体的教学设计（详见文1），深受启发，笔者实践跟进，也从这种整体观的思路出发，构思了“平行线的性质”的教学设计，提供研讨.

一、“平行线的性质”教学设计

（一）对前面所学的判定方法进行复习回顾，并为新课的学习做准备.

活动1：学生回顾已学的平行线的判定.

已知结论

判定1同位角相等，两直线平行.

判定2内错角相等，两直线平行.

判定3同旁内角互补，两直线平行.

角的数量关系⇒两直线的位置关系

（相等或互补）（平行）

活动2：回顾判定的学习过程，包括引导学生回顾判定1为公理，由它推出判定2、判定3.

设计思考：让全体学生对前一节的内容和方法进行回顾，为学生能将学习的经验迁移到新课中做好准备.

（二）通过猜想、画图、测量、比较，让学生获得较强的感性认识，便于探索两直线平行的性质定理.

活动1：反过来，如果两条直线平行，同位角、内错角、同旁内角各有什么关系呢？（抛出问题，让学生作出猜想，引出课题）

活动2：请每位同学利用手中的练习本，任意选取其中的两条平行的线作l1、l2，再随意画一条直线l3与l1、l2相交，用量角器量得图中的八个角，检验刚才的猜想是否正确.

随后同桌之间交换，再次测量，汇报结果.

【解读】教师提出问题，引导学生分析，自己动手，实际操作，进行度量、观察，在有了大量感性认识的基础上，动脑分析总结出结论.不仅充分发挥了学生的主体作用，培养了学生观察、分析问题的能力，还培养了学生的实践探究能力.

（三）由学生描述发现的结论，并给予证明，以锻炼学生的归纳、表达能力，鼓励学生敢于发表自己的观点.

活动1：让学生对发现的结论给予较为准确的文字表述.

两直线平行，同位角相等.

两直线平行，内错角相等.

两直线平行，同旁内角互补.

教师说明：与平行线的判定1相同，“两直线平行，同位角相等”也是人们从长期实践中得出的结论，不需要证明，称之为“公理”.它是平行线的性质1.

平行线的性质1：两条平行线被第三条直线所截，同

位角相等.简称：两直线平行，同位角相等.

符号语言：如图1，直线a、b被直线c所截，由a∥b（已知），得∠1=∠2（或∠5=∠6，∠3=∠4，∠7=∠8）（平行线的性质1）.

活动2：让学生对比上节课利用“同位角相等，两直线平行”推出“内错角相等，两直线平行”，小组合作交流如何用平行线的性质1推出“两直线平行，内错角相等”和“两直线平行，同旁内角互补”.

图1

问题1：已知：如图1，a∥b.求证：∠4=∠5.

证明：由a∥b（已知），得∠1=∠2（两直线平行，同位角相等）.

又∠1+∠5=180°，∠2+∠4=180°（平角定义），则∠4=∠5（等角的补角相等）.

想一想，如何由∠1=∠2推出∠2=∠7？

（学生小组研究，派代表讲解）

（结论）平行线的性质2：两条平行线被第三条直线所截，内错角相等.简称：两直线平行，内错角相等.

符号语言：直线a、b被直线c所截，由a∥b（已知），得∠4=∠5（或∠2=∠7）（平行线的性质2）.

问题2：已知：如图1，a∥b，求证：∠2+∠5=180°.

证法1：由a∥b（已知），得∠1=∠2（两直线平行，同位角相等）.

又∠1+∠5=180°（平角定义），则∠2+∠5=180°（等量代换）.

证法2：由a∥b（已知），得∠2=∠7（两直线平行，内错角相等）.

又∠7+∠5=180°（平角定义），则∠5+∠2=180°（等量代换）.

（结论）平行线的性质3：两条平行线被第三条直线所截，同旁内角互补.简称：两直线平行，同旁内角互补

符号语言：直线a、b被直线c所截，由a∥b（已知），得∠2+∠5=180°（或∠4+∠7=180°）（平行线的性质3）.

活动3：讨论这些性质定理与前面所学的判定定理有什么不同，避免出现概念的混淆，渗透“命题”与“逆命题”的概念，突破本节课的难点.

【解读】给学生留有充分的探索和交流的空间，鼓励学生利用多种方法探索，这对于发展学生的空间观念，理解平行线的性质是十分重要的.在推理的过程中培养学生的逻辑思维能力以及严谨的治学态度，逐步锻炼学生的推理能力，并进一步巩固对定理的理解及语言的规范.

（四）在学生理解了平行线的性质的基础上，教师进一步创设情境，提供数学材料，帮助学生进一步体会平行线的判定与性质之间的区别.

活动：练习巩固（题目略）.

（五）小结阶段，引导学生回顾学习活动过程，整体建构平行线知识体系.

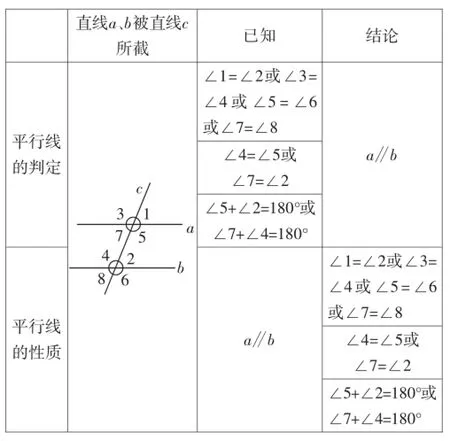
二、教学立意解读

笔者曾在文4中以“等腰三角形的性质”教学为例，倡导章建跃先生提出的为学生构建“逻辑连贯、前后一致”的学习过程，让学生形成数学“整体观”.文章得到一些同行的共鸣，以下再围绕上文课例就相关观点做出进一步的阐释.

1.基于数学知识的“逻辑连贯、前后一致”开展“单元教学”

在本节课学习之前，学生已经了解了平行线的概念，知道了平行公理及其推论，并且有了平行线判定的学习经验，所以本节课平行线性质定理的学习，学生通过知识的迁移学起来会比较轻松.本节“平行线的性质”是空间与图形领域的基础知识，在以后的学习生活中会经常用到，所以确定“平行线的性质”作为本节课的重点.由于学生是第一次接触“性质定理”，且这些“性质定理”与前面的“判定定理”互为逆命题，所以很容易将本节内容与前面的知识混淆.因此，区分平行线的性质定理与判定定理就被确定为本节课的难点.事实上，这也是我们将平行线的性质预设成一节单元教学的原因，而没有像教材上那样把几个不同的性质定理分开“逐个教学”.

2.引导学生辨明知识的生长点，并构建知识框架传递“整体观”

找准知识的生长点，创设恰当的问题情境是重要的，同时学生从实践中得到的知识印象最深刻，所以上面引入新知时还注意通过让学生先度量、猜想再引入定理，让学生通过探索活动来发现结论，经历知识的“再发现”过程.在实验的基础上，组内同学相互帮助、争论、提示，鼓励学生利用性质1对性质2、3进行说理、论证.为了逐步深入地让学生学会说理，落实重点，突破难点，编排了一些练习题，逐步锻炼学生的推理能力，并进一步巩固对定理的理解及语言的规范，能够进行推理证明.作为课堂最后，通过表格梳理的方式把平行线的判定与性质并列在一起进行比较，这也是践行章建跃先生在《数学教育之取势明道优术》一文中倡导的“教好数学”内涵：“为学生构建前后一致、逻辑连贯的学习过程，使学生在掌握数学知识的过程中学会思考，……在面对一个新的数学研究对象时，要有‘整体观’，要先为学生构建研究的整体框架.”

三、结束语

新世纪以来的课改已进入第二个十年，然而在这十多年当中，由于初中数学各种版本教材的“推陈出新”，一线教师又忙于应付各级考试的“现实引领”，这使得“课改必须改课”再次被提到重要位置，是机械教条地迎合教材并“教教材”，还是基于“理解数学”的高度重组教材并“用教材教”？这需要广大同行共同努力.我们提供的关于“单元教学”的案例只是抛砖引玉，不一定准确，更不一定正确，期待更多的批评指正和实践跟进.

1.章志霞.基于“整体观”的几何教学与反思——以“平行线的判定”教学为例［J］.中学数学（下），2015（2）.

2.李庾南.自学·议论·引导教学论［M］.北京：人民教育出版社，2013.

3.吉明华.重视逻辑连贯，促进自主学习——以“等腰三角形的轴对称性”教学为例［J］.中学数学（下），2014（4）.

4.章建跃，陈向兰.数学教育之取势明道优术［J］.数学通报，2014，52（10）.

5.钟启泉.新旧教学的分水岭［J］.基础教育课程（上），2014（2）.Z