一道中考几何压轴题的解法探究和亮点赏析

☉江苏省海门市海南中学 杨春鸟

一道中考几何压轴题的解法探究和亮点赏析

☉江苏省海门市海南中学 杨春鸟

随着数学新课程标准的深入实施，为提高考试的区分度，直线型几何综合题越来越受到全国各地中考命题专家的青睐，涌现出不少好题.以下是笔者对2014年南通市中考数学试题第27题的解法探究和亮点赏析.

一、原题呈现

题目：（2014年南通）如图1，矩形ABCD中，AB=3，AD=4，E为AB上一点，AE=1.M为射线AD上一动点，AM=a（a为大于0的常数）.直线EM与直线CD交于点F，过点M作MG⊥EM，交直线BC于点G.

图1

（1）若M为边AD的中点，求证△EFG是等腰三角形；（2）若点G与点C重合，求线段MG的长；

（3）请用含a的代数式表示△EFG的面积S，并指出S的最小整数值.

二、解法探究

先解决第一问.

思路：先证明EM=FM，再证明EG=FG.

方法1：利用相似和中垂线的性质.

由M为AD的中点，得AM=DM.由四边形ABCD是矩形，得AB∥CD.所以=1，即EM=FM.又因为MG⊥EF，所以GE=GF，所以△EFG是等腰三角形.

方法2：利用全等.

同方法1，可得AB∥CD.故∠A=∠FDM，∠AEM=∠DFM.又AM=DM，所以△AEM≌△DFM.所以EM=FM.因为MG⊥EM，所以∠GME=∠GMF.又因为GM=GM，所以△EMG≌△FMG.

所以EG=FG.所以△EFG是等腰三角形.

方法3：利用三角函数.

再由中垂线的性质或全等证得EG=FG.

评析：尽管三种方法思路一样，但从简洁的角度看，“先利用相似或三角函数，再根据中垂线的性质”证明方法更为直接，相对烦琐的是用两次全等证明.

再解决第二问.

思路：建立关于a的方程.方法1：利用相似.

若点G与点C重合，如图2，由四边形ABCD是矩形，得∠A=∠ADC=90°.

所以∠AEM+∠AME=90°.

由MG⊥EF，得∠CME=90°.所以∠CMD+∠AME=90°.

图2

方法2：运用勾股定理.

由MG⊥EM，得ME2+MG2=EG2.

又ME2=AE2+AM2=1+a2，MG2=DM2+DG2=（4-a）2+9，EG2=BE2+BG2=4+16=20，所以1+a2+（4-a）2+9=20.解得a=1或a=3.

方法3：建立平面直角坐标系.

以B为坐标原点，BA、BC所在直线为y轴、x轴，建立如图3所示的平面直角坐标系.

由AE=1，AB=4，AM=a，得E（0，2）、M（a，3）.

图3

由MG⊥EM，设直线MG：y=-ax+c，将C（4，0）代入，得-4a+c=0，则c=4a.

所以直线MG：y=-ax+4a.将M（a，3）代入，得-a2+4a= 3.解得a=1或a=3.

评析：方法1利用相似三角形的对应边成比例建立方程，方法2利用勾股定理建立方程，思路都比较直接，学生容易想到，但学生的易错点是方法1中的找准“对应边”、方法2中的正确“数式计算”.方法3建立平面直角坐标系，将问题转化为求出直线MG的解析式，解答过程也较简洁，且运算要求不高，该方法实在是妙，但对思维水平和解题策略的要求较高，一般学生不易想到.

方法1：直接求△EFG的底边和高.

①当点M在线段AD上时，如图4，过M作MH⊥BC于H，可得△HMG∽△AME.

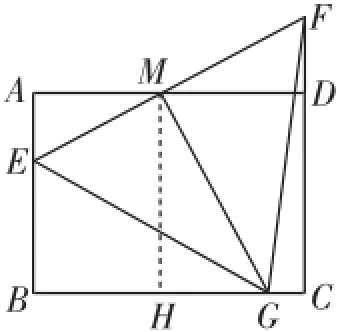
图4

②当点M在线段AD的延长线上时，如图5，过M作MH⊥BC于H，下同①中方法（略）.

图5

评析：此解法通过作垂线，构造相似三角形，利用相似三角形的对应边成比例直接求出△EFG的底边和高.学生较易想到这样的思路，但解答过程不简洁，且对运算要求偏高，已经超出了教材和数学课程标准的要求，笔者认为该方法不可取，大部分学生难以顺利地推出正确的答案.

方法2：将△EFG的面积转化为同底且底边平行于矩形的一边的两个三角形.

①当点M在线段AD上时，如图6，作GH⊥AD于H，并延长交直线EF于P.

图6

②当点M在线段AD的延长线上时，如图7，作GH⊥AD于H，并延长交直线EF于P.

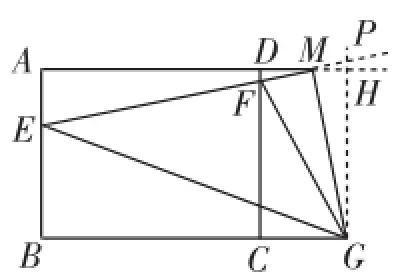
图7

评析：此解法尽管也是通过作垂线，构造相似三角形，利用相似三角形的对应边成比例直接求出相关的线段长，但变直接求为间接求面积，即将△EFG的面积分割转化为同底且底边平行于矩形的一边的两个三角形的面积之和或差，达到了化繁为简、化难为易的目的.笔者认为这种方法是求解图形面积的常用招数，也是基础方法.

方法3：利用整体与部分的关系，将△EFG的面积转化为整体与部分的差.

图8

所以S=S梯形EBCF-S△BEG-S△FCG

②当点M在线段AD的延长线上时，如图9，作FH⊥AB于H，则利用S=S梯形HBCD-S△BEG-S△HEF同样可求得.

图9

评析：此解法为“图形补充法”，即将所求原图形填补一个或多个特殊（或可求）图形，使其变为一个新的特殊（或可求）图形，而后用新图形的面积减去所补图形的面积，可得所求原图形的面积，体现了“化生为熟”的转化目的.笔者认为这种方法也是求解图形面积的常用方法，但对学生的运算能力要求较高，心态平和才能圆满地解答出来.

三、亮点赏析

（1）本题是以矩形和三角形为基础，以动点为背景求函数关系的问题，主要考查学生运用运动变化的思想去探究问题中不变的数学元素.本题综合性较强，将相似三角形（全等三角形）的性质和判定、矩形的性质等知识融为一体，实现了对“直线型”几何知识的综合考查，对观察能力、逻辑推理能力、方程与函数思想、数形结合思想和分类讨论思想有较高的要求，同时也考查了学生的学习经验，突出数学的思维价值，作为压轴题有较好的区分度.

（2）试题的呈现自然、简洁、和谐，凸显了对数学本质的思考，设计的3个问题有层次性，体现了压轴题的选拔功能.试题的第一问比较容易，大部分学生能轻松解决；第二问难度中档，成绩中上等的学生能较好地解决；第三问是本题作为压轴题的难点和精彩所在，对学生的解题能力和思维深度提出了较高的要求.一是要求学生对运动的特点要有深刻的理解，考查了学生的几何想象能力和画图能力；二是要抓住关键词“射线”，准确判断运动过程中点M和相应的点G的两种情况，考查了学生分类讨论的数学思想；三是要确定运动中不变的因素，沿着设置的“路标”按图索骥，再探索△EFG的面积的求法，如直接法、分割法、面积相加和相减法等，考查了学生数形结合的数学思维方式；四是要运用相似三角形或解直角三角形的方法表示相关线段的函数关系，渗透了方程与函数的数学思想方法；五是要经过正确的代数运算才能得到最后的结果，考查了学生的计算能力和心理素质.

（3）本题每一问均能从不同的角度考虑，能探索到不同的解决问题的方法和策略，而第二问中一反常态地“建立平面直角坐标系”，为本题注入了新的活力，第三问中求面积时，直接求解过程的烦琐和利用“割”“补”等方法将原图形进行转化后达到柳暗花明、豁然开朗的感觉，这些解法的灵活性、发散性和不同的解法带来的不同的结果对一线教师的教学有很好的导向作用.在平时的教学中，在关注通解、通法的基础上，还要加强学生的联想能力和猜想能力，比如看到平行线联想到相似；看到高、垂线联想到面积、勾股定理、平面直角坐标系等，由这些知识出发可以进一步寻求其他不同的解题路径和方法，打破思维定势，激发学生换一种角度，培养学生思维的灵活性和发散性.

1.周晓慧，苑建广.图形面积的多重角色释读——以2013年中考试题为例［J］.中学数学（下），2014（6）.

2.顾洪敏，刘金英.一道中考题赏析［J］.中国数学教育（初中版），2011（11）.