“五、四、三、二”在圆中的妙用

☉江苏省东海县横沟中学 霍如本

“五、四、三、二”在圆中的妙用

☉江苏省东海县横沟中学 霍如本

“圆”是图形与几何体系中重要的一部分内容，近些年来，各地中考数学试卷通过圆本身具有特殊的轴对称性与旋转对称性设置各种试题，突出对圆的基本性质的直接考查；通过将三角形与四边形放在圆中设置综合问题，实现对直线型图形的综合应用与再认识的过程，突出体现了对图形与几何的综合运用的考查.

在教学的过程中很多教师都会遇到此类状况：教学时花了很多时间，学生做了很多练习，可学生掌握的就是不好，遇到圆的考题得分不高.笔者认为原因在于“圆”这一章概念多，学生难以完全掌握，即使知道相关结论运用起来也找不准突破口.基于此状况，通过长时间的教学，笔者认为在此章的教学时，需用特殊的记忆方式进行总结，让学生快速掌握此章的精髓，故在教此章时提出了四字记忆法：五、四、三、二.“五”即为五种多解情形，“四”即为四个常用结论，“三”即为三个公式，“二”即为两种常见作图.在此方法教学过程中再加上必要的典型例题，从最后的考试评价上分析是有效的.

一、“五”——五种多解

1.由于点与圆的位置关系不确定而产生多解

点与圆的位置关系有三种：点在圆内、点在圆上、点在圆外，考试中常出现点与圆的位置关系题目，故要分情况考虑某点在圆内或圆外．

例1（鄂州）平面上一点P到⊙O上一点的距离最长为6cm，最短为2cm，则⊙O的半径为______．

分析：解答此题应进行分类讨论，点P可能位于圆的内部，也可能位于圆的外部．

2.由于点在圆上的位置不确定而产生多解

圆是很特殊的图形，它不仅是中心对称图形而且是轴对称图形，同时圆具有旋转不变性，故一点在圆上时要考虑是否有其余可能的情况存在．

例2已知⊙O的半径为1cm，弦AB、AC的长度分别为2cm、1cm，则∠BAC=_____°．

分析：此题要确定点C的位置，由于点C在圆上的位置出现不唯一性，所以要进行分类讨论．

3.由于弦所对弧的优劣不确定，所对的圆周角的类型不确定而产生多解

圆中的弦、弧、角有着密切的关系，在中考中常被作为必考考点，一条弦（非直径）对应一个圆心角，但对应两类弧，有优劣之分，此时这两类弧又分别对应相应的圆周角，故提到弦所对的弧或圆周角时常要分类讨论.

例3（泰安改编）⊙O的半径为1，AB是⊙O的一条弦，且AB=1，则弦AB所对圆周角的度数为______．

分析：一条弦对两条弧，两条弧又对应相应的圆周角，故此题会有多解．

4.由于两平行弦与圆心的位置不确定而产生多解

垂径定理的应用在圆中十分广泛，常用于求圆中某弦的长度或弦心距，这类题中又常出现一种分类讨论的题目：求两平行弦间的距离．由于圆是轴对称图形，故两条平行弦可能在圆心同侧或异侧，这样就出现了分类讨论．

例4已知⊙O的半径为5cm，弦AB∥CD，AB=6cm，CD=8cm，则AB和CD的距离为_____．

分析：由于AB、CD的位置不明确，所以分平行弦在圆心的同侧（如图1）和圆心的两侧（如图2）两种情况讨论．

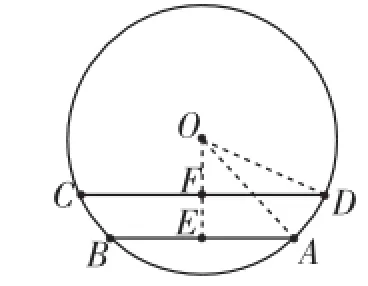
图1

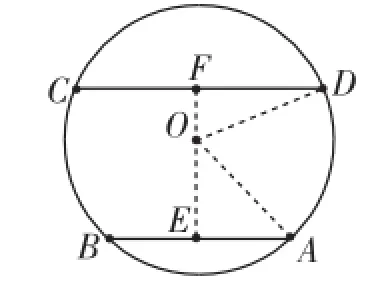
图2

5.由于直线与圆相切的位置不确定而产生多解

直线与圆相切的考题常以运动中的直线或圆出现，在运动的过程出现多次相切，故需要进行分类讨论．

例5如图3，在平面直角坐标系中，x轴上一点A从点（-3，0）出发沿x轴向右平移，当以A为圆心、半径为1的圆与函数y=x的图像相切时，点A的坐标是______．

分析：由于⊙A与直线相切的位置可以在直线的左侧也可以在右侧，故需要分类讨论．

图3

二、“四”——四个结论

苏科版教材将圆中的相交弦定理、弦切角定理、切割线定理、割线定理、公切线定理等删除，从而降低了学生掌握圆的难度，也让教师更容易归纳出四个重要结论的用途．

1.垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的弧

垂径定理的作用是：常用于圆中求长度的题目，如求半径、弦长、弦心距、两平行弦间的距离等．还可以让学生了解到求圆内线段常用垂径定理和勾股定理，求圆外线段用相似．

例6如图4，AB是⊙O的一条弦，AB= 6，圆心O到AB的距离为4，则⊙O的半径为_______．

2.圆心角、圆周角一系列定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，是圆心角的一半；直径所对的圆周角是直角；90°的圆周角所对的弦是直径

图4

圆心角、圆周角一系列定理的作用是：常用于求某些角的度数或转换圆中的角，并可以达到直角和直径间的互相转换．

例7如图5，AB是圆的直径，点C在圆内，请仅用无刻度的直尺画出△ABC中AB边上的高．

3.切线的判定定理：经过半径的外端，并且垂直于这条半径的直线是圆的切线

图5

判定一条直线是圆的切线的方法有3种，切线的判定定理是最常用的一种，一般情况下，判断一条与圆有公共点的直线是圆的切线常用此方法证明．

例8如图6，AB为⊙O的直径，C为⊙O上一点，AD和过C点的直线互相垂直，垂足为D，且AC平分∠DAB．

（1）判断直线DC与⊙O的位置关系，并说明理由；

（2）若OA=6，AD=10，求CD的长．

4.切线长定理：从圆外一点引圆的两条切线，它们的切线长相等

遇到从一点引出的两条圆的切线的题目常用切线长定理，不仅可以得到相等的线段，也能得到相等的角．

例9如图7，AB、BC、CD都是⊙O的切线，点A、D为切点．已知AB= 4，BC=7，则CD=_____．

图6

图7

三、“三”——三个公式

3.圆锥侧面积公式：S侧=πrl

例10用一个半径为6，圆心角为120°的扇形围成的圆锥的底面圆半径为______．

例11已知圆锥的底面半径为1cm，母线长为3cm，则其侧面积为（）.

A．πcm2B．3πcm2

C．4πcm2D．6πcm2

四、“二”——两种作图

1.复原一个“圆”

圆中有这样一种作图：作出一个破损的圆形物件所在圆的圆心或将它所在的圆补充完整，这就要利用结论“不在同一直线上的三个点确定一个圆”.

例12某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，图8是水平放置的破裂管道有水部分的截面．

图8

（1）请你补全这个输水管道的圆形截面；

（2）若这个输水管道有水部分的水面宽AB=16cm，水面最深地方的高度为4cm，求这个圆形截面的半径．

2.作出已知三角形的外接圆、内切圆

无论作一个三角形的外接圆还是内切圆，首先要确定圆心，外接圆圆心为三角形三边垂直平分线的交点，内切圆圆心为三角形三个内角平分线的交点，再根据半径作圆即可．

心理学研究表明，提高记忆力的方法可以用联想记忆法：利用事物间的联系通过联想进行记忆的方法．联想是由当前感知或思考的事物想起有关的另一事物，或者由头脑中想起的一件事物，又引起想到另一件事物．由于客观事物是相互联系的，各种知识也是相互联系的，因而在思维中，联想是一种基本的思维形式，是记忆的一种方法．通过“五、四、三、二”的学习，让学生将互相接近的“圆”的概念与数字产生联想．用联想来增强记忆，这样学生掌握起来更加容易．

事实上，初中生的思维发展正处于一个由具体到抽象、由低级到高级的过程．学生思维中的形象或表象通过积累将逐步让位于概念，并由经验型的抽象逻辑思维逐步向理论型的抽象思维发展转化．这一发展转化离不开具体的形象，故笔者认为在教学中，要善于运用合适并能促进学生快速记忆的方法进行教学，而“五、四、三、二”的教学法就是一个好的方法，它让学生记住了深奥的圆中有关的知识，事半功倍，真正达到了学生的轻松学习.Z