动手操作动脑思考手脑并用显奇效——例论初中数学实验在数学考试中的体现

☉江苏省张家港市港区初级中学 黄嘉玲

动手操作动脑思考手脑并用显奇效
——例论初中数学实验在数学考试中的体现

☉江苏省张家港市港区初级中学 黄嘉玲

“人有两件宝，双手和大脑；双手能做工，大脑能思考”,这是陶行知先生对手脑并用的最精辟的论述.手脑并用的教学方法不仅在平时的教育教学过程中发挥着巨大的功用，如今的中考数学也更注重考查学生动手动脑的能力.以下笔者将通过数学实验的操作过程，实例论述中考数学中出现的手脑并用的操作类问题.

一、先动手再动脑，折叠剪贴见奇妙

图形的折叠问题是中考中的重要考点，蕴藏着丰富的内涵，此类问题的解决思路是：根据轴对称图形的特点和折叠前后图形的不变性，指导学生进行有规律的动手操作，操作按照步骤进行，抓住折痕这一关键点，折痕即是对称轴，轴对称变化前后图形的大小和形状都不会发生改变.动手折叠不仅有利于培养学生的动手操作能力，更有利于培养学生的观察、发现、分析、解决数学问题的综合能力.下面以中考实例阐述：

例1（2014年某地中考题）正方形纸片进行如下折叠，按照从左到右的顺序，最后将折叠的纸片沿虚线（直角三角形的中位线）将上面的小直角三角形用剪刀剪去，如图1.将留下的纸片展开，得到的图形是图2中的（）.

图1

图2

此题可以让学生通过剪纸游戏感性地找出正确答案，通过“双手来做工，大脑来思考”的过程，反复思考将具体形象思维转化成抽象思维，在大脑中形成过程痕迹，每次动手之后都有一个动脑的过程，在教学中长期坚持，学生的形象思维和想象力都会相应提高.而动手的目的是为了锻炼学生的大脑，发展思维能力.通过这一过程答案A显而易见.

二、先动脑再动手，明确目的见成效

实际学习中有些问题必须在学生充分动脑之后才可以动手操作，这就要求教师在教学环节设计上下功夫，如果备课中没有明确的目的和安排，操作时就会缺乏目的性，在一定程度上还会禁锢学生的思维，限制学生的发展.下面再以一个中考实例来论述说明：

例2（2015年某地中考题）如图3是一个正方形，我们沿虚线将其剪开（x＜y）得到①②③④四块图形，用以上的四块图形恰能拼成一个非正方形的矩形.

（1）请你把满足这样条件的图形画出来；

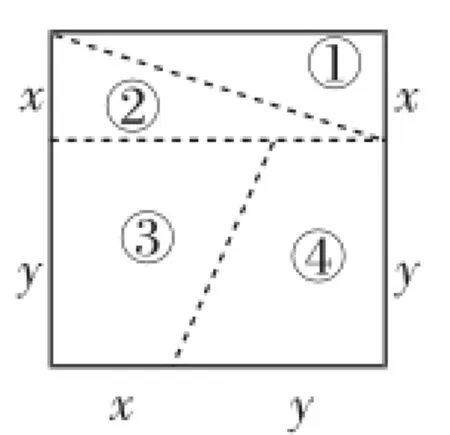
图3

分析：抓住关键的知识点进行阅读是解决此题的关键：①可以通过图形前后面积不变建立相应的方程；②拼图的时候注意观察，可以考虑把相同的边拼在一起.此题全面考查了学生的动手和观察解决问题的能力，解放学生思维的同时给于他们足够的动手和动脑的空间.

解：（1）如图4.

（2）方法一：根据所拼图形的面积前后相等得［（x+y）+y］y=（x+y）2.

图4

以下同解法一．（以上给出的是简易的解题过程）

在处理此类问题的时候，我们可以大胆地把主动权交给学生来处理，学生在操作过程中可以进行度量，自己进行尝试不同的拼接方法，在不断的尝试中寻找最终最优的解决问题的方式和方法，从而提升了学生解决问题的能力和逻辑思维的能力.当这样的问题得到解决之时，学生各方面的能力一定也会得到长足的进步，新课程标准中所提到的创新精神和动手能力自然而然地得到了潜移默化的提升.

三、边动手边动脑，手脑并用效果好

动手动脑的过程是一个整体过程，显然是密不可分的.如果遇到有困难的问题，在探究过程中存在一定的难度时，反复操作寻找思路是一个不错的方法.

例3（2014年江苏省无锡市中考题）（1）请你仔细观察：小明同学将三角形纸片ABC（AB＞AC）沿过点A的直线进行折叠，使AC落在AB边上，折痕为AD，将纸片展开（如图5）；再次折叠该纸片，使点A与点D重合，得到折痕EF，展开纸片后得到△AEF（如图6）．小明认为△AEF是等腰三角形，你同意这个结论吗？请说明理由．

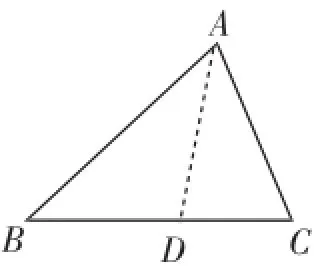
图5

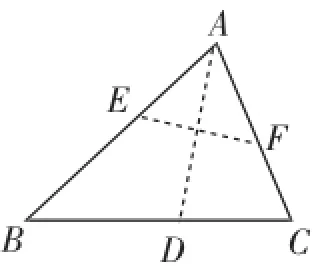
图6

（2）实践与运用：将矩形纸片ABCD沿过点B的直线折叠，使点A落在BC边上的点F处，折痕为BE（如图7）；再沿过点E的直线折叠，使点D落在BE上的点D′处，折痕为EG（如图8）；再展平纸片（如图9）．求图9中∠α的大小．

图7

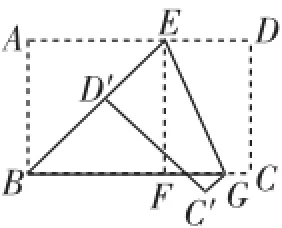
图8

图9

分析：笔者参加了中考该题的阅卷工作，对于此题印象非常深刻：学生给出的答案五花八门，而且多数解法非常复杂，没有很好地从头脑中找到逻辑推理的思路.试想：如果让学生借助操作通过动手剪拼，动脑思考，很好地利用轴对称的性质，就会很自然地想到解题方法.由此可见，动手与动脑只有协调互动，学生的思维能力和操作能力才会相应地提高.

通过分析，动手折叠，很快就能发现解决的方法：只要抓住折叠前后角的大小不变，细心找相等的角，该题就迎刃而解.

解：（1）同意．如图10，设AD与EF交于点G．

由折叠知，AD平分∠BAC，所以∠BAD=∠CAD．

又由折叠知，∠AGE=∠DGE=90°.所以∠AGE=∠AGF=90°.

所以∠AEF=∠AFE，所以AE=AF.

即△AEF为等腰三角形．

（2）由折叠知，四边形ABFE是正方形，∠AEB=45°，所以∠BED=135°．

又由折叠知，∠BEG=∠DEG，所以∠DEG=67.5°．

从而∠α=90°-67.5°=22.5°．

从这个问题的解决过程我们可以看到，手和脑一旦协调起来，思维和操作的过程自然而然就能够跟上，几何解题和书写能力的提升也是显而易见的.

图10

四、反思数学实验与数学思维

可见，数学实验是课堂教学中为探究或验证某个数学猜想、解决某类数学问题、获得某种数学理论所采取的一种方式方法，他的核心是让学生开动脑筋，做数学操作，也就是正常的动手动脑过程.通过数学实验，可以适度降低学生探索数学问题的难度.在实验过程中，学生可以通过操作与体验，积累基本的活动经验，加深对数学的领悟与理解，培养发现与提出数学问题的能力，进而提升数学素养.可以说数学学习最终的目的是培养学生分析问题和解决问题的能力，将所学知识运用到生活当中，解决实际问题.数学实验作为一种方式之一，它能帮助学生增进对数学的理解.在开展数学实验教学的过程中，要让学生参与实验，要让学生思考，要给学生思考的机会.唯有如此，才能让学生的思维活动走向深刻.所以，在操作活动中突出的是“数学实验活动的外化”与“数学思维品质的内化”相互统一的教育哲学观点.因此，数学实验教学应突出让学生经历数学化的过程，让学生从自身的数学经验出发，经过自己的思考，主动去获得一些发现和感悟.

1.张维忠.文化视野中的数学与数学教育［M］.北京：人民教育出版社，2005.

2.孔凡哲，史宁中.关于几何直观的含义和表现形式——对《义务教育数学课程标准（2011年版）》的一点认识［J］.课程·教材·教法，2012（7）.

3.王希平.重视几何直观揭示几何图形性质［J］.数学通报，2005（2）