类氖氙离子LMn双电子复合模拟谱

杨建会， 范 强， 张建平

(乐山师范学院物理与电子工程学院， 乐山 614004)

类氖氙离子LMn双电子复合模拟谱

杨建会， 范 强， 张建平

(乐山师范学院物理与电子工程学院， 乐山 614004)

在双电子复合过程发生的能量范围内，发射X光子的原子过程除双电子复合过程外还有辐射复合、共振激发、共振复合以及直接激发原子过程. 本文使用相对论组态相互作用方法计算了这些过程的截面，比较了在双电子复合过程发生的能量范围内这些原子过程的截面与双电子复合过程截面，探讨了这些过程对双电子复合过程的影响. 研究结果表明，辐射复合截面随入射电子束能量的增大迅速减小，在双电子复合能量范围内几乎为一常数，可以作为本底来处理；共振激发和共振复合过程对双电子复合过程的影响可以忽略不计；当入射电子束能量高于靶离子的第一激发能时，电子碰撞直接激发截面与高Rydberg态的截面连成一片，随着入射电子束能量的增加，电子碰撞直接激发截面越来越大，这时必须考虑直接激发过程. 使用相对论组态相互作用方法计算了类氖氙离子的双电子复合截面，其结果与已有的部分实验和理论结果很吻合.

相对论组态相互作用； 双电子复合； 截面

1 引 言

双电子复合 (dielectronic recombination, DR)过程对中高电子温度、中低电子密度等离子体中建立和维持热等离子体的电离平衡以及离子激发态布居起重要作用. 在孤立共振和独立过程近似下，双电子复合可以表示为以下两步， 第一步，通过俘获一个自由电子，同时激发一个束缚电子形成一个双激发自电离态的复合离子，也即是自电离的逆过程；第二步，从双激发自电离态通过辐射衰退到不可再自电离的态则完成双电子复合过程. 双电子复合过程通常可以用KLL，LMN，LMO等描述，LMO双电子复合过程指自由电子被俘获到O壳层，同时激发L壳层上的一个电子到M壳层形成双激发自电离态的双电子复合过程. LMn(n=3, 4, 5…)双电子复合过程是类氖离子双电子复合的主要过程，LMn双电子复合对类氖离子总双电子复合速率系数的贡献占90%左右[1-3]. 由于类氖离子的电离阈能比LMn共振的共振能高1倍以上，甚至可以达到LMM共振能的2-3倍，而且LMn共振过程具有较多的中间态，比如对LMM共振过程就有273个中间态，因此LMn共振过程不容易被观察到. 随着实验手段的提高，实验仪器的改进，1990年，Schneider等人才首次在实验中测量到了类氖金离子的LMM共振过程[4]. DeWitt等人以及Asada等人使用电子束离子阱(EBIT)分别在1992年和1997年发现了类氖氙离子的LMn双电子复合过程[5, 6], 并使用多组态Dirac Fock (MCDF)方法计算了其截面. 本文使用相对论组态相互作用方法研究了类氖氙离子的LMn共振过程，讨论了在双电子复合过程发生的能量范围内，伴随双电子复合过程发生的与发射光子有关的辐射复合、共振激发、共振复合、直接激发过程的截面，确定这些过程对双电子复合过程的影响.

2 理论方法和计算过程

类氖氙离子的LMn双电子复合过程表示为

2s22p6(i)+e→(2s2p)73lnl′(j)

→2s22p6nl′(k)+hν

(1)

2s22p6(i)+e→(2s2p)73lnl′(j)

→2s22p63l(k)+hν

(2)

式(1)和(2)分别表示从2p或2s上激发一个电子并同时俘获一个自由电子形成的中间态(2s2p)73lnl′通过内壳层或外壳层辐射跃迁至单激发类钠离子，(2s2p)7表示n= 2壳层上比满电子壳层少一个电子.i→j→k双电子复合过程的双电子复合截面为

(3)

随着入射电子能量的增加，在高能量区域，类氖氙离子会发生电子碰撞直接激发(direct excitation, DE)，根据相对论组态相互作用计算，类氖氙离子2s22p6到(2s2p)73l的第一个激发能级的激发能是4207.37 eV. 在入射电子能量高于4207.37 eV时，通过以下过程能观测到X射线

1s22p6(i)+e→(2s2p)73l(b)+e′

(2s2p)73l(b)→1s22p6(i)+hv

(4)

在本文中，只讨论了最低的(2s2p)73l激发态，没有考虑激发到更高的(2s2p)73l激发态，计算中使用扭曲波近似方法处理连续态[7]. 对每一个跃迁的电子碰撞激发强度使用四参数拟合公式，对于自旋允许的跃迁，电子碰撞激发强度表达式为

(5)

对于自旋禁止的跃迁，电子碰撞激发强度表达式为

Ωib=p0xγ

(6)

其中

(7)

(8)

p0，p1，p2，p3为四个拟合参数，b是Bethe 系数，对非偶极允许跃迁，b=0，对于自旋禁止跃迁b为负数，Ee是入射电子能量，Eib是碰撞激发前后能级的能量差.

电子碰撞激发(DE)截面与碰撞强度Ωib之间的关系为

(9)

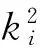
(10)

(11)

除了直接激发过程外，还将发生共振激发和共振复合过程，以下我们讨论伴随LMP双电子复合过程发生的共振激发(resonant excitation, RE)和共振复合(resonant recombination, RER)过程，共振激发过程是双电子激发态通过自电离到激发态，激发态再通过辐射衰退到低激发态，其过程为

2s22p6(i)+e→(2s2p)73l6l′(j)→(2s2p)73l(b)+e′

(2s2p)73l(b)→2s22p6(k)+hv

(12)

共振激发截面为

(13)

考虑到入射电子能量的Gaussian分布，则

(14)

另外，双电子共振激发态如果通过两次连续的辐射衰退到单激发稳态则完成共振复合过程，其具体过程为

2s22p6(i)+e→(2s2p)73l6l′(j)→(2s2p)73l6l′(j′)+hv

(2s2p)73l6l′(j′)→2s22p66l′(k)+hv′

(15)

因为j′仍然是双激发态，所以可以通过自电离或辐射退激发到单激发态，因此在计算共振复合过程的截面时应该还要考虑j′的辐射分支比，共振复合过程的截面可以表示为

(16)

考虑到入射电子能量的Gaussian分布，则

(17)

另外，在实验中伴随双电子复合过程发生的还有辐射复合(radiativerecombination,RR)过程，

2s22p6(i)+e→2s22p6nl(k)+hv

(18)

辐射复合过程是光致电离(photoionization,PI)的逆过程，其截面可以使用以下公式来计算

(19)

其中

(20)

(21)

其中L是多极跃迁算符的秩，[L]=2L+1，S是线强

(22)

其中k是自由电子的相对论量子数，JT是自由态的总角动量，OL是多极算符[8]. 相关的原子结构数据，包括能级，自电离几率，辐射跃迁几率，有效碰撞强度的计算使用相对论组态相互方法的FAC (flexible atomic code)程序计算[7, 9, 10]，连续态使用扭曲波方法，该程序广泛使用于研究复杂离子的原子过程[11-14].

3 结果与讨论

为了确定在双电子复合能量范围内，共振激发，共振复合对双电子复合的影响，图1作出了LMP入射电子能量范围的双电子复合，共振激发，共振复合过程的截面. 图中点线表示双电子复合截面，短划线表示共振复合截面，实线表示共振激发截面. 从图1可以清晰的看出，共振激发和共振复合过程的截面比双电子复合过程的截面要小得多，共振激发和共振复合过程对双电子复合过程的影响可以忽略不计；因此在实验和理论的比较时通常忽略共振激发和共振复合过程是合理的.

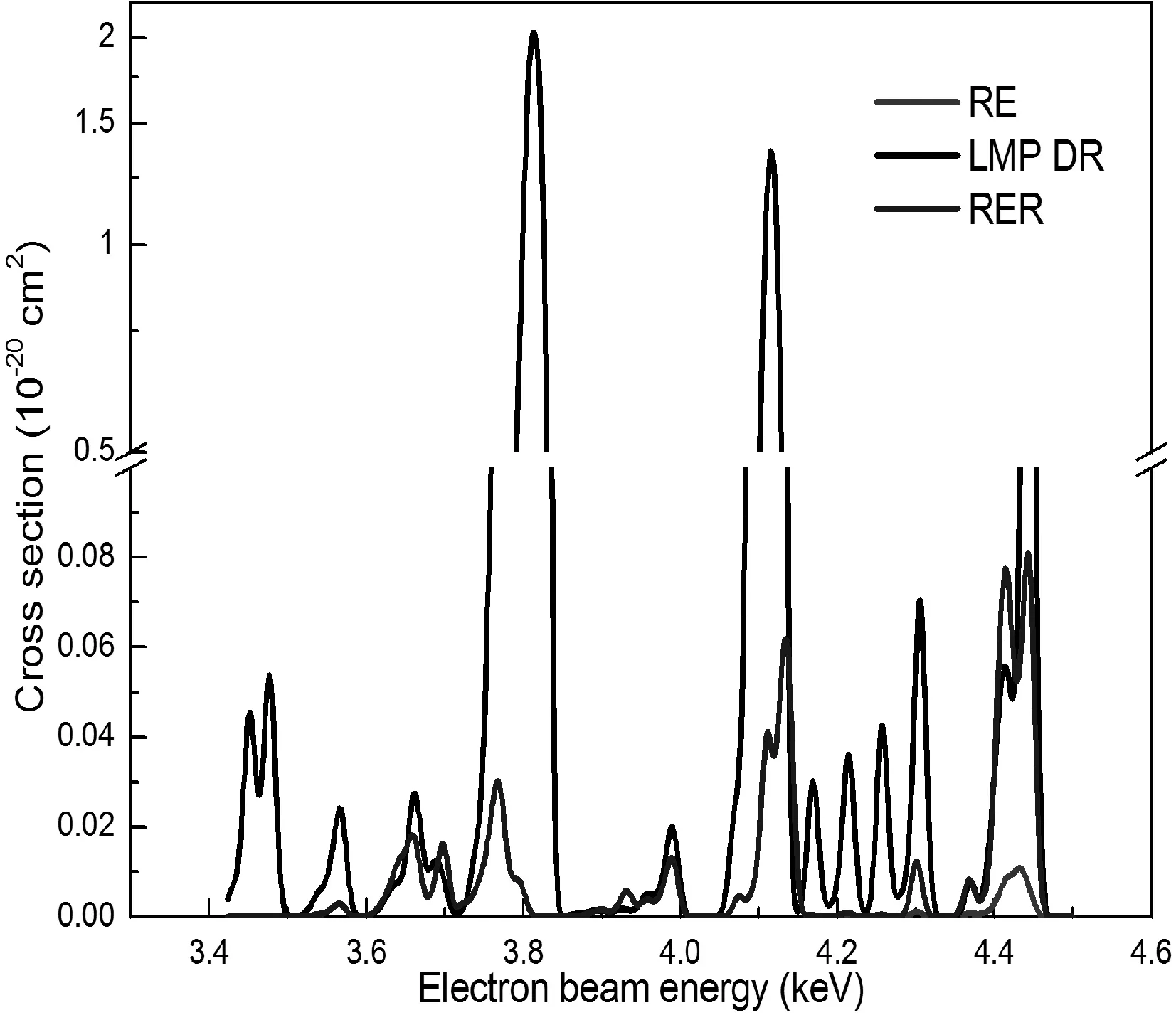
图1 LMP双电子复合(LMP DR)，共振激发(RE)，共振复合(RER)截面，FWHM=16.2 eVFig. 1 Cross section of LMP dielectronic recombination (LMP DR), resonant excitation (RE) and resonant recombination (RER), FWHM=16.2 eV

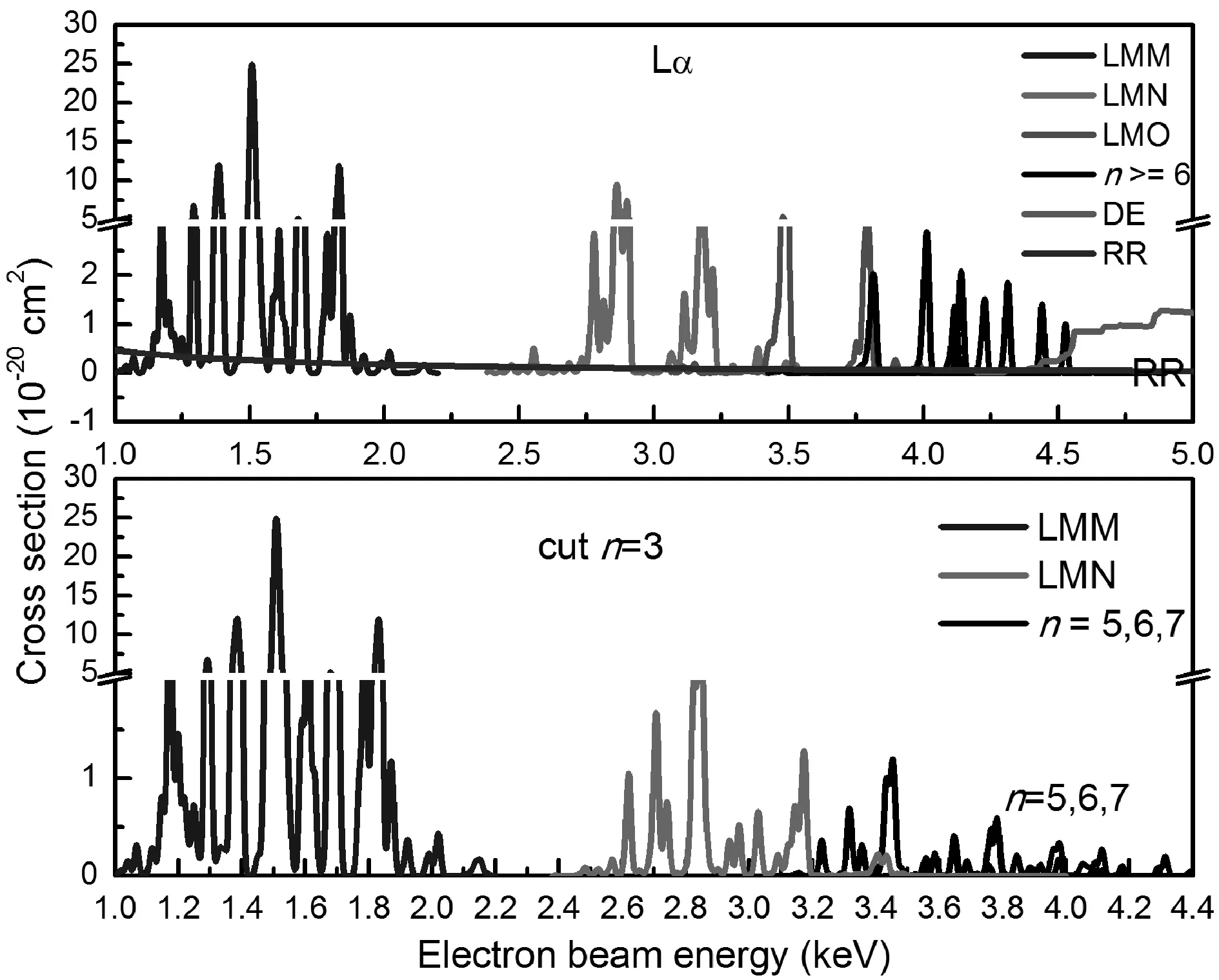
图2 LMn双电子复合截面，FWHM=16.2 eV，(a)内壳层退激，包括DE和RR过程，(b)外壳层退激Fig. 2 Cross section of LMn dielectronic recombination, FWHM=16.2 eV, (a) inner-shell deexcitation, include DE and RR processes, (b) outer-shell deexcitation

图2给出本文所计算的类氖氙离子的LMn双电子复合截面，(a)图表示通过内壳层退激发的类氖氙离子的LMn双电子复合截面，包括电子碰撞激发截面，辐射复合截面；(b)图表示通过外壳层退激发的类氖氙离子的LMn双电子复合截面.

对于(2s2p)73lnl′双激发自电离态，随着n的增加，相邻组态之间的能量差越来越小，从图2清晰的看出，n>6的LMn双电子复合过程不能区分开，而且高Rydberg态的截面将和DE截面连成一片，其原因可以解释如下：对于高Rydberg双电子激发自电离态，内壳层电子的辐射退激发几率变成常数，而外壳层电子的辐射退激发几率可以忽略不计，自电离衰退几率与n-3成正比，因此高Rydberg双电子激发态的辐射分支比趋近于一个常数，考虑到电子能量的Gaussian分布后，通过高Rydberg双电子激发态的双电子复合截面为

(23)

由于高Rydberg双电子激发态组态相邻组态之间的能量差很小，因此高Rydberg双电子激发态自电离态不容易区分开，在较高的电子能量范围，可以将高Rydberg双电子激发态看做是连续态. 辐射复合截面在双电子复合能量范围内几乎为一常量，可以作为本底来处理；当入射电子束能量高于靶离子的第一激发能时，电子碰撞直接激发截面与高Rydberg态的截面连成一片，随着入射电子束能量的增加，电子碰撞直接激发截面越来越大，这时必须考虑直接激发过程.

1992年DeWitt等人，使用EBIT实验测得到类氖氙离子的LMn双电子复合截面，并与多组态Dirc-Fock(MCDF)方法计算结果进行了比较[6]，如图3给出了本文使用的相对论组态相互作用(RCI)方法计算得到的类氖氙离子LMM双电子复合截面结果和EBIT实验和MCDF理论结果. 其中，实线是本文计算结果，虚线是MCDF方法计算结果，点是EBIT实验值. 从图3可以看出本文所计算的截面和已有的实验和理论值符合得很好. 本文计算的总LMN, LMO, LMP, LMQ双电子复合截面作于图4.

图3 LMM双电子复合截面，FWHM=16.2 eVFig. 3 Cross section of LMM dielectronic recombination, FWHM=16.2 eV

图4 总LMn(n=3, 4, 5,6)双电子复合截面，FWHM=16.2 eVFig. 4 Total cross section of LMn(n=3, 4, 5,6) dielectronic recombination, FWHM=16.2 eV

4 结 论

本文使用相对论组态相互作用方法，计算了类氖氙离子的双电子复合谱，并讨论了在双电子复合过程发生的能量范围内，伴随双电子复合过程发生的发射X光子的辐射复合、共振激发、共振复合以及直接激发原子过程，比较了在双电子复合过程发生的能量范围内这些原子过程对双电子复合过程的影响. 研究结果表明，辐射复合截面随入射电子束能量的增大迅速减小，在双电子复合能量范围内几乎为一常数，可以作为本底来处理；共振激发和共振复合过程对双电子复合过程的影响可以忽略不计. 当入射电子束能量高于靶离子的第一激发能时，高Rydberg态的截面和电子碰撞激发截面连成一片，且随着入射电子束能量的增加，电子碰撞直接激发截面越来越大，这时必须考虑直接激发过程. 使用相对论组态相互作用计算可到类氖氙离子的双电子复合谱，结果与已有的部分实验和理论结果很吻合.

[1] Yang J H, Fan Q, Zhang J P. The study of dielectronic recombination (DR) rate coefficient for ground state of Ne-like isoelectronic sequence ions [J].ActaPhys.Sin., 2012, 61(19): 193101 (in Chinese) [杨建会, 范强, 张建平. 类氖等电子系列离子基态的双电子复合速率系数研究[J]. 物理学报, 2012, 61(19): 193101]

[2] Yang J H, Cheng X L, Deng B L. Detailed level-by-level study of dielectronic recombination for Ne-like gold [J].Phys.Scr., 2010, 81(1): 15304.

[3] Wu H, Yang J H, Zhang J P,etal. Detailed level-by-level study of dielectronic recombination for neon-like tungsten [J].J.SichuanUniversity:Natural

ScienceEdition, 2012, 49(4): 843 (in Chinese) [吴华, 杨建会, 张建平, 等. 类氖W64+离子基态双电子复合过程的细致能级计算[J]. 四川大学学报: 自然科学版, 2012, 49(4): 843]

[4] Schneider M B, Knapp D A, Chen M H,etal. Measurement of the LMM dielectronic recombination resonances of neonlike gold [J].Phys.Rev. A, 1992, 45(3): R1291.

[5] Asada J, Currell F J, Fukami T,etal. X-ray spectroscopy at the Tokyo electron beam ion trap [J].Phys.Scr., 1997, 1997(T73): 90.

[6] Dewitt D R, Schneider D, Chen M H,etal. Dielectronic recombination cross sections of neonlike xenon [J].Phys.Rev.Lett., 1992, 68(11): 1694.

[7] Gu M F. Dielectronic recombination rate coefficients for H-like through Ne-like isosequences of Mg, Si, S, Ar, Ca, Fe, and Ni [J].Astrophys.J., 2003, 590(2): 1131.

[8] Gu M F. The flexible atomic code III. Photoionization and radiative recombination: Private communication[J].NrcResearchPress, 2008.

[9] Gu M F. Electron-impact excitation of Fe XXII: Comparative study of relativistic R-matrix and distorted-wave approaches [J].Phys.Rev. A, 2004, 70(6): 62704.

[10] Gu M F. IndirectX-ray line-formation processes in iron L-shell ions [J].Astrophys.J., 2003, 582(2): 1241.

[11] Yang J H, Zhang H, Cheng X L. The KLL dielectronic recombination processes for highly charged krypton, iodine and barium ions [J].Chin.Phys. B, 2010, 19(6): 63201.

[12] Zhang Y, Chen C Y, Wang Y S,etal. Resonance excitation process for Ni-like gold [J].J.Quant.Spectrosc.Radiat.Transfer, 2009, 110(18): 2180.

[13] Ran Z G, Gao C, Zeng J L. Study on the KLL dielectronic recombination process of Li-like ions [J].J.At.Mol.Phys., 2010, 27(3): 418 (in Chinese) [冉贞贵, 高城, 曾交龙. 类锂离子KLL双电子复合过程研究[J]. 原子与分子物理学报, 2010, 27(3): 418]

[14] Deng B L, Jiang G, Wang W. Spectrum simulation of Li-like oxygen plasma [J].HighPowerLaserandParticleBeams, 2009, 21(8): 1230 (in Chinese) [邓邦林, 蒋刚, 王巍. 类Li氧等离子体光谱模拟[J]. 强激光与粒子束, 2009, 21(8): 1230]

Dielectronic recombination spectrum of neon-like xenon

YANG Jian-Hui, FAN Qiang, ZHANG Jian-Ping

(School of Physics and Electronic Engineering, Leshan Normal University, Leshan 614004, China)

The atomic processes emitting X-photon include radiative recombination (RR), resonant excitation (RE), resonant recombination (RER) and direct excitation (DE) within the energy range of dielectronic recombination (DR). The cross sections of those atomic processes were calculated by using relativistic configuration interaction (RCI) method. We compared cross sections of those atomic processes with that of DR process, and analyzed the influence of those processes on DR process. The results show that the RR cross section decreases with the increase of electron beam energy quickly; within the energy distribution of DR process, the RR cross section is almost a constant, which can be treated as background; the effect of RE and RER can be negligible; with the increase of electron beam energy, the cross section of electron impact DE becomes large, the DR cross section can’t distinguish from high Rydberg states; the cross section of electron impact become larger and larger with the increase of electron beam energy. The dielectronic recombination spectrum of neon-like xenon was calculated by using relativistic configuration interaction (RCI) method; the corresponding present results are in good agreement with reliable values within the inaccuracy.

Relativistic configuration interaction (RCI) method; Dielectronic recombination; Cross section

103969/j.issn.1000-0364.2015.12.006

2014-01-18

四川省科技厅资助项目(2011JYZ005)；四川省教育厅资助项目(15ZA0273, 13ZB0111)；乐山师范学院人才启动科研项目(Z1165, Z1273)

杨建会(1980—),女，四川绵竹人，博士，副教授，主要从事原子结构与光谱方向研究.E-mail: yjh20021220@foxmail.com

范强.E-mail: fq20021220@foxmail.com

O562.4； O562.1

A

1000-0364(2015)06-0931-05