一道试题解法的精彩演绎
☉州高新区孙红
一道试题解法的精彩演绎
☉江苏省苏州市高新区第一中学孙红
一、原题呈现
例1(1)如图1,若BC=6,AC=4,∠C=60°,求△ABC的面积;
(2)如图2,若BC=a,AC=b,∠C=α,求△ABC的面积;
(3)如图3,在四边形ABCD中,若AC=m,BD=n,对角线AC、BD交于O点,它们所成的锐角为β,求四边形ABCD的面积.

图1
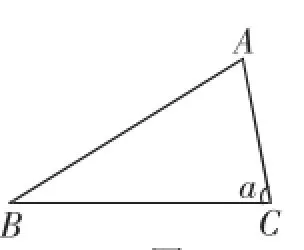
图2
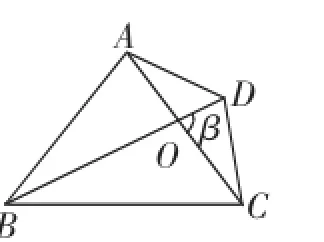
图3
说明:这是《中学数学》(下)2014年第8期文1给出的一道关于三角函数方面的复习题.
评析:本题源自高中课本,主要目的是引导学生经历从特殊到一般的过程去探索并发现三角形的面积公式SbcsinA,然后运用所发现的面积公式求已知对角线及其夹角的四边形的面积,这也是一个拓广应用的过程.本题由问题(1)到问题(2)凸显了从特殊到一般的归纳思想,从问题(2)中的三角形面积到问题(3)中的四边形面积充分体现了化归思想,因此,本题对培养学生形成良好的数学思维品质具有很好的作用.

图4
文1给出了它的常规解法之后,展示了学生给出的精彩解法.为了说明问题,这里只抄录精彩解法,常规解法此处从略.
精彩解法:如图4,过点C作BD的平行线,在平行线上取CM= BD,过点A作AN⊥CM,垂足为N,易得S四边形ABCD=S△ACM.
因为CM∥BD,所以∠ACM=∠AOB=β.
思考:不论是常规解法还是精彩解法,均符合题目考查的意图,即考查学生发现数学结论,并应用所发现的结论解决实际问题的能力,实现这一意图的基本途径就是将四边形的面积转化为三角形的面积计算.笔者通过研究学生的上述解法后发现,学生给出的解法确实很精彩,其精彩之处在于巧妙地将四边形的面积转化为三角形的面积来计算.这一精彩的解法是从哪里来的呢?
文1认为:“本题给予了一个全新的知识体系,用了一种全新方法求面积,紧扣学生认知区域的边缘,知识覆盖面大、综合性强,故对学生具有一定的难度,但正因为有一定的难度,所以才能很好地‘逼’出了学生的思维.”学生的思维果真能被“逼”出来吗?其实,学生已经有了给出这种解法的基础知识、基本技能、基本思想和基本数学活动经验.
二、追根溯源
1.立足教材,落实“四基”
平行四边形是初中阶段非常重要的平面图形,不仅要求学生理解平行四边形的边、角、对角线所具有的性质,而且要求学生能够灵活运用这些性质解决实际问题.学生在探索平行四边形性质和判定的过程中,已初步积累了一定的基本数学活动经验,具备了解决平行四边形有关问题的基本技能.学生已经知道通过添加平行四边形的对角线,可将一个平行四边形分成两个全等三角形.由此可知,一条对角线将平行四边形分成两个面积相等的三角形.在此基础上,学生也探索过关于平行四边形面积的其他性质.因此,关于平行四边形的面积问题,学生已具有以下基础知识:
(1)如图5,四边形ABCD是平行四边形,连接一条对角线AC,则S△ABC=S△ACD.
(3)如图7,点O是▱ABCD内任意一点,则S△AOB+
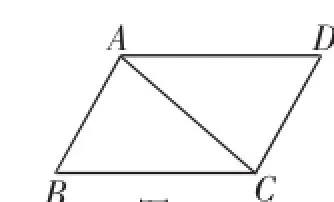
图5
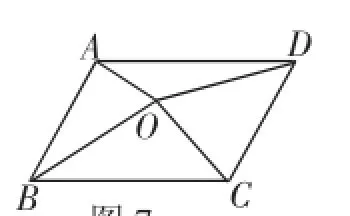
图7
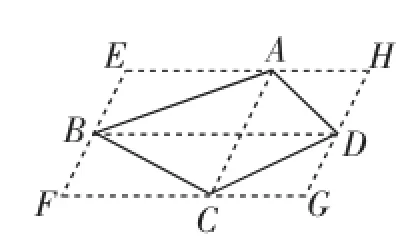
图8

图6
以上三条性质虽然简单,但在解决实际问题中有着重要的作用.
北京师范大学出版社出版的《义务教育教科书·数学》(八年级下册)161页有这样的一道习题:
例2如图8,某村有一个四边形池塘,它的四个顶点A、B、C、D处均有一棵大树,村里准备开挖池塘建鱼塘,想使池塘的面积扩大一倍,又想保持大树在池塘边不动,并要求扩建后的池塘成平行四边形的形状,请问能否实现这一设想?若能,请你设计出所要画的图形;若不能,请说明理由.
解析:如图8所示,连接AC、BD,过点A与点C分别作BD的平行线,过点B与点D分别作AC的平行线,四条平行线两两相交于点E、F、G、H,则四边形EFGH是平行四边形.由平行四边形的性质易知,S▱EFGH=2S四边形ABCD.因此,这一设想能够实现.
点评:本题是在学生学习了平行四边形的性质之后,经常见到的图形设计问题,它主要考查学生运用平行四边形的性质解决实际问题的能力,只要学生理解了平行四边形面积的有关性质,在教师的积极引导下学生容易完成作图,然后根据平行四边形的面积所具有的性质很容易说明四边形ABCD与平行四边形EFGH面积之间的关系.通过这类问题的解决,可以为学生解决与之类似的数学问题积累一定的数学基本活动经验.
2.演绎精彩
鉴于以上的基础知识和数学活动经验,可给出例1问题(3)的如下解法:
如图9,过点A与点C分别作BD的平行线,过点B与点D分别作AC的平行线,四条平行线两两相交于点E、F、G、H,由平行线的性质及平行四边形的定义易知,四边形EFGH是平行四边形,连接FH,易知EH=BD=n,EF=AC=m,∠E=β.
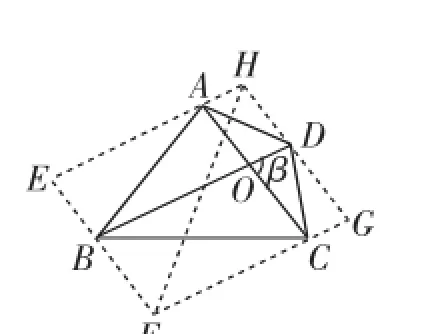
图9
学生给出的解法又是怎么来的呢?将图9中的▱ACGH沿D■→B方向平移|D→B|个长度单位,使GH与EF重合,点A的对应点为L,点O的对应点为K,点C的对应点为M,得到图10.由平移的性质易知,四边形ACML是平行四边形,图9中四边形ABCD的面积与图10中△ABC、△BML的面积和相等.

图10
在上述解答过程中,如果只将图9中的点G沿D→B方向平移|D→B|个长度单位,就会得到图4,由此可得到学生给出的精彩解法.
三、结束语
精彩的解法不会从天而降,更不会从学生的思维中被“逼”出来,它源于对数学基础知识的牢固掌握,源于对数学基本思想方法的深刻领会,源于对基本数学技能、基本数学活动经验的积累.因此,在数学教学中,一定要认真落实《义务教育数学课程标准》(2011年版)所倡导的数学理念,立足教材,重视基础知识,注重渗透数学思想方法,有意识地引导学生领会归纳、类比、转化等常用思想方法,并将其运用在问题的解决过程中,积累学生基本技能与基本数学活动经验,也就是要认真落实“四基”,使学生真正获得适应社会生活和进一步发展所必需的数学基础知识、基本技能、基本思想和基本活动经验.
1.李海燕.换个解法更精彩[J].中学数学(下),2014(8).
2.中华人民共和国教育部制定.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012.
3.张宁.关注核心知识重视基本方法——2013年宁夏中考数学试题评析[J].中学数学(下),2013(12).H

