精心预设,精巧引导,精彩演绎
——对一节“全等三角形”阶段性复习研讨课的思考
☉浙江省杭州市启正中学 郑娟
精心预设,精巧引导,精彩演绎
——对一节“全等三角形”阶段性复习研讨课的思考
☉浙江省衢州市实验学校詹 金芳
☉浙江省杭州市启正中学 郑娟
这是一节来自2014年“浙派”名师班关于阶段性复习的研讨课,上课老师为我们展示了一节别样的“全等三角形”复习课.现将课堂实录与笔者的思考整理成文,供同行们交流研讨.
一、课堂实录

图1
1.视频引课
课堂一开始,老师让同学们观看视频,视频中一位老师作如下讲述.
同学们,我们今天研究一个有趣的话题,我随手画一个三角形,能证明所画的三角形是等腰三角形.同学们相信吗?下面请看我的证明.如图1(视频中老师徒手画图),任意画三角形ABC,则有AB=AC.对于这个问题,我是这样思考的,只要作∠BAC的平分线和BC边上的中垂线,两线交于点O,BC边上的中垂线交BC于点D,过点O分别作AB和AC的垂线段,垂足分别为E和F,连接OB、OC.同学们,接下来请你们试试看:能证明AB=AC吗?
视频放到这儿,上课教师按下暂停键,并对同学们说:“同学们,相应的题目和图形请看学习单,你能接下去完成这个题目的证明吗?”学生一听这些话可来劲了,个个嘴里都在嘀咕着“怎么可能呢?”说着说着,教室里的声音渐渐地变小了,大家都投入到对问题的证明中去了,几分钟后,声音又渐渐大了起来,部分同学皱着眉头低声地交流:“好像真的能证明耶!奇了怪了!”看到许多同学完成证明却又有疑惑时,教师叫停了大家,并让同学们继续看视频.
根据刚才添加的辅助线,我们可以很快证明出△AOE≌△AOF,同学们,你能说明理由吗?
上课教师再次按下暂停键,并让同学们说明两个三角形全等的理由.
生1:由OA平分∠BAC,得∠EAO=∠FAO.
由OE⊥AB,OF⊥AC,得∠OEA=∠OFA=90°.
由OA=OA,∠EAO=∠FAO,∠OEA=∠OFA,得△AOE≌△AOF(AAS).
教师追问:“还有别的方法吗?”
生2提出可以用“ASA”定理加以证明;生3根据角平分线的性质得到OE=OF,从而利用HL定理证明.教师对证明稍作梳理后再次按下视频播放键.
同学们,前面已证明了AE=AF,而要证明AB=AC,只要再证明BE=CF,那么如何证明这两条线段相等呢?通常证明两条线段相等会从两个三角形全等出发,也就是证明△BOE≌△COF,这成为解决问题的关键,同学们,你能解决该问题吗?
上课教师继续让学生分析证明的思路.
生4:由OD是线段BC的垂直平分线,得OB=OC.
由OE=OF,∠OEB=∠OFC=90°,OB=OC,得△BOE≌△COF(HL).
教师总结:生4用“HL”定理给予了证明,你还有其他的证明方法吗?同学们发现只要抓住直角三角形这一特征,可以将条件进行转化(由OE=OF,OB=OC,∠OEB=∠OFC=90°,可以获得BE=CF这一结论),进而分析可以用“SAS”的判定方法进行证明.此时,教师继续追问:能否直接证明△BOA与△COA全等?同学们通过分析发现满足的条件是“SSA”,从而否定了这个思路.在这个环节中,教师与学生一起复习和梳理了全等三角形所有的判定方法和注意点.
通过上面的证明我们可以获得AB=AC这一结论,我们同样也可以证明BA=BC和CA=CB,这样不就可以说明△ABC是等边三角形了吗?这显然是不成立的,问题到底出在哪儿呢?
生5:老师,我觉得证明没有问题,关键在画图上.
此话一出马上得到同学们的附和,有的说老师是徒手画的三角形,不准;也有的说角平分线画得不准;还有的认为角平分线和中垂线的交点位置好像有问题.
老师顺势归纳,既然图形有问题,那么你能画一个准确的图加以验证吗?
2.作图验证
老师结合同学们的发现作进一步的分析,尽管原图是徒手画的,三角形的边被画歪了,但是三角形的三个顶点的位置是固定的,你能用尺规在学习单的空白处画出一个三角形,使所画的三角形与原图中连接三个顶点所得的三角形全等吗?
同学们纷纷动手画图.老师要求尺规作图有困难的同学可以与同桌合作完成,并请一同学在黑板上进行了演示(图形大小按视频中的进行截取,为表述方便,所作三角形仍然用△ABC表示).师生一起回顾了尺规作三角形的基本步骤,而后引导学生分别作∠BAC的平分线和BC边上的中垂线,进一步复习作角平分线和线段的中垂线的相关知识.同学们通过作图发现:∠BAC的平分线和BC边上的中垂线的交点O在△ABC的外部,而并不像视频中所反映的点O在△ABC的内部.此时才恍然大悟,原来问题出在作图上.对此,教师进一步归纳:生活中有很多直观看到的未必就一定是真实的,我们应该用数学的原理进行规范作图和证明,才能发现问题的根源.
3.提炼升华
教师在完成对问题的分析、讲评和归纳的基础上再追一问:“同学们,我们是否可以总结出任意三角形其中一个角的平分线和这个角的对边的中垂线的交点一定在三角形的外面呢?”
这一问题再次将同学们的思维推向新的高度.同学们立刻动起手来,分别画出锐角三角形、直角三角形和钝角三角形进行尺规作图,通过实践操作获得结论:对于任意的三角形,其中一个角的平分线和这个角的对边的中垂线的交点一定在三角形的外面.
老师继续追问:“通过作图我们发现上述结论是正确的,但是怎么证明呢?我们不是学过,要说明一个命题是真命题必须给予证明吗?”
这一下把学生难倒了,所有学生都有一种“知其然而不知其所以然”的感觉,一时间全班陷入了证明说理的困境中.
看到学生一筹莫展,教师进一步引导,我们学过说明一个命题是真命题必须给予严格的证明,而当我们感到直接证明十分困难时,是否该换个思考方式呢?
经此点拨,部分优秀学生立刻找到了解题的思路——反证法.
生6:我们可以用反证法证明.假设交点在△ABC的内部,那么根据我们前面的证明,就能说明它是一个等边三角形(学生边讲边上黑板画图,如图2),其交点重合于点O(学生误把点O当成满足条件的交点).因此,只有正三角形其交点在三角形的内部,否则,交点必定在三角形的外部.
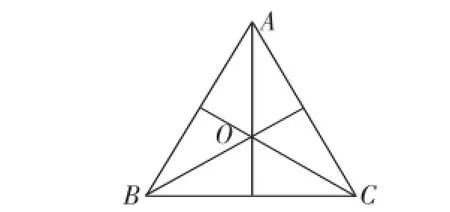
图2
该同学的回答得到了同学们的认可,并获得全班同学热烈的掌声.正当同学们得意时,老师泼了一盘冷水:“这个同学的观点正确吗?”
此话一出,同学们面面相觑,表现出很惊讶的眼神.
不久,生7发表观点:我们知道等边三角形一个角的平分线和该角的对边的中垂线是重合的;同时,我们再看本节课开始的问题,假如AB=AC,那么根据等腰三角形的性质我们可以得到∠BAC的平分线和BC边上的中垂线也是重合的.由此可知,等腰三角形其顶角平分线(所在的直线)和底边上的中垂线是重合的;若不是等腰三角形,其交点一定在三角形的外部.
生7的发言再次赢得全班热烈的掌声.教师在此基础上进行了课堂小结:本节课我们通过一个网络视频,对一个错误的数学结论进行推理论证,在这个过程中复习了尺规作图和三角形全等证明的相关知识,通过进一步的探究,发现并证明了三角形的一个拓展结论.同时,本节课也告诉我们许多时候直观感觉是有欺骗性的,我们应该学会用数学手段和方法对问题进行严密的论证.同学们可以将我们本节课研究问题、获得结论的方法用于平时生活和学习之中,你定能有新的发现和收获.
二、笔者的反思
1.教师精心的课前预设和精巧的教学引导激发了学生精彩的课堂演绎
本节课将一个网络微视频作为引课素材,将视频中教师演绎证明的内容进行删减,把证明过程留给学生完成,达到了引出问题、制造悬念、激发兴趣的目的,引课环节可谓另辟蹊径,方法独到.
视频中,教师徒手画图的设计意味深长,倘若在实际教学中,教师定然不能徒手草率画图给学生以负面的影响,这样的设计也为后续学生对问题的研究提供了很好的平台,徒手画图,图不准导致学生不易发现问题之所在,促使学生在问题研究时需要对图形提出更高的要求,为尺规作图的引出作好了铺垫.
教学中,教师根据学生的课堂生成因势利导,将学生的思维不断引向深刻.学生从对假命题的证明中产生了强烈的认知冲突,在作图中发现了问题所在,在拓展思考中探究出一般规律,从而达到将问题进行提炼升华的目的,整个教学设计可谓立意新颖、构思巧妙.
教师的课堂语言极其精炼,只在必要时作适当的引导和总结,教师的组织者、引导者和合作者的地位得到很好的体现.学生课堂参与性好,主体地位得到充分的展现.教师给出视频,引出本节课的研究对象,便放手让学生探究证明;完成证明后引导学生探寻产生认知冲突的根源;找到原因后教师只作面上的引导,让学生从中发现一般规律;在探究规律的过程中,教师仍然放手让学生去尝试,只在学生有困难处加以点拨.在教师巧妙的引导下,出现了一节学生参与度高,多次迸发思维火花的高效课堂.可以说,在教师精心的预设和精巧的引导下,学生的思维得以精彩的演绎.
2.关注“四基”的落实,突出理性精神的培养,促进学生能力的发展
本节课十分关注课程标准提倡的“四基”的落实,注重对全等三角形知识(全等三角形的判定和尺规作图)的应用与整理,重视学生动手能力的培养,关注尺规作图这一基本技能的落实,渗透了研究问题的基本思想方法.本节课十分关注研究问题方法的指导,说明一个命题是真命题,需要严格的推理论证;当证明结果与实际不符时,引导学生追根溯源.在探寻问题的根源时,需要用科学的原理和方法,这样的教学渗透了发现和提出问题、分析和解决问题的基本思想和方法,促进了学生能力的全面发展.研究问题时,从具体的研究对象入手(不同类型的三角形),归纳出一般的结论(角平分线和该角的对边的中垂线的交点在三角形外面),在对问题进行论证时又从一般走向特殊(从一般三角形到等腰、等边三角形),渗透了研究问题的方法和角度.本节课十分关注对学生理性精神的培养,让学生明白了“直观与演绎”的关系,进一步感受直观是用于发现猜想,演绎才能证明结论;没有演绎,直观往往会成为错觉,只有将直观与演绎进行完美的结合,才能揭示事物的本质特征.
3.一个视频引出一个问题,理出一章的知识,这是一种有效的复习教学模式
教师从一个网络视频出发,引出一个研究课题:证明任意一个三角形都是等腰三角形,让学生从一开始就产生认知上的冲突,从而紧紧抓住这一冲突,不断设置思维障碍,引导学生进行探究;在问题探究过程中,为完成AB=AC的证明,教师引导学生复习三角形全等的判定;为验证教师所画的图形有问题,引导学生复习尺规作图的相关知识.可以说通过对一个错误结论的研究发现,将全等三角形的知识进行了系统的复习和整理.这样的复习教学避免了枯燥乏味的知识梳理和简单机械的解题训练,通过对一个有趣问题的探究充分调动了学生学习的积极性,并在问题研究过程中达到复习和梳理知识点的目的,实在是一种值得提倡的复习课教学模式.
4.值得探讨的方面
这是一节高水平的阶段性复习研讨课,值得学习的地方很多,当然也有值得商榷和研讨的地方.就本节课而言,本人提出以下方面与同行商讨.
操作活动方式是否过于单一.整节课教师为达到完成梳理尺规作图的教学目标,将学生用于发现问题的操作方式限制于尺规作图,而忽略其他操作方式的应用,如可以允许学生利用刻度尺和量角器进行度量,从而画出相应的角平分线和中垂线,也可以将三角形纸片进行折叠从而产生角平分线和中垂线.对操作方法的限制其实是对学生思维的限制,对学生发散性思维的培养极为不利.
教学方式是否过于单一.以教师提问与引导,学生独立探究和师生互动交流的方式贯穿整节课,学生间的合作与交流、生生间的互助等学习方式较少,这样的教学对班级部分后进学生的学习不利.Z