一道填空题引发的思考

一道填空题引发的思考

☉山东省聊城第六中学扈保洪

据文1称，某区九年级第一学期期末数学统考试卷中，有一道满分为2分的填空题，经考试后分析，在某一所中等水平学校的472名学生中，该题只有一人得满分，零分率高达99.8%.不仅如此，笔者发现，文1在分析了该题目的来龙去脉后，所给出的解答过程也是不严谨的.因此，本文也对该题的解法作些分析，并进行适当地推广.现整理出来，与同行交流.

一、试题呈现

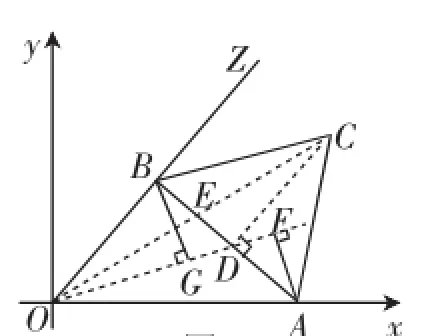
图1

题目如图1，在平面直角坐标系xOy中，已知正三角形ABC的边长为2，点A从点O开始，沿x轴的正方向移动，点B在∠xOy的平分线OZ上移动，则点C到原点O的最大距离是_____.

二、解题思路探究

图2

1.从正面探究

（1）对于上述填空题，文1的作者联想到了以下的引例.

引例：如图2，已知正三角形ABC的边长为2，两顶点A、B分别在平面直角坐标系的x轴、y轴的正半轴上滑动，点C在第一象限，连接OC，求OC长的最大值.

在图2中，求OC长的最大值的思路为：“取AB的中点D，连接CD、OD，则OC≤OD+ CD，因为易知OD=1，CD=，两者均为常数，所以当滑动AB而使OC经过点D时（此时OC⊥AB），OC的长度最大，此时OC=OD+CD=1+”.基于此，文1认为只要简单地类比上述做法，就能找到图1中OC的最大值.但笔者却发现，问题没那么简单.因为若像在图2中那样，先取AB的中点D，并连接CD、OD，虽有OC≤OD+CD，但由∠xOZ=45°知，当△ABC的边AB滑动时，CD是常量，而OD是变量，从而使OD+CD也是变量，所以当OC⊥AB时，尽管有OC=OD+CD，仍不能直接说明OC最大！显然，要想说明此时的OC最大，还必须说明此时的OD最大.对此进一步探究如下：

①在图1中，过点A、B分别作OD的垂线，垂足分别为点F、G，由勾股定理得OA令∠BDG=β，OD=t）.而根据三角形面积公式，知AB·OD·sinβ=OA·OB· sin45°，代入数值化简整理，得（1+t2）2=4t2+4t2sin2β≤8t2，又得1+t2再由该不等式的解集与其所对应的二次函数图像的关系，知这表明OD的最大值是

（此时sinβ=1，得∠BDG=β=90°）.因此，当OC⊥AB时，OC确实最大，最大值为

图3

②如图3，设OC⊥AB，若沿Ox、OZ随意滑动AB的端点，得△ABC的一个新位置记为△A1B1C1，A1B1的中点记为D1，分别连接DD1、OD1，并分别作BB1、DD1的垂直平分线，两线相交于点K，则△A1B1C1就是将△ABC以点K为旋转中心，沿顺时针方向旋转而得到的.此时，再连接D1E，根据垂直平分线的性质，显然有OD=OE+ED=OE+ D1E>OD1，再根据△A1B1C1位置的任意性，从而说明OD的值最大.

（2）在图1与图2中，既然都是当OC⊥AB时，OC的长最大，那么能否在图2中OC最大的基础上，通过两图间的联系推出图1中OC的最大值呢？

如图4，设OC⊥AB，以原点O为旋转中心，把△ABC沿顺时针方向旋转22.5°得到△A1B1C1，则由前面的讨论知再过A1、B1分别作OC1的平行线，分别交Ox、OC于点A2、B2，连接A2B2，则易知A1A2=OA1=0B1= B1B2=且A1A2∥B1B2，A1A2⊥A1B1，故四边形A1B1B2A2为矩形，A2B2=A1B1=2；在射线上OC1截取C1C2=，分别连接B2C2、C2A2，得△A2B2C2，因易知四边形A1A2C2C1、B1B2C2C1均为平行四边形，故△A2B2C2≌△A1B1C1，从而C1C2是△A1B1C1沿射线OC1所能平移的最大距离（否则，边A2B2的端点将不在∠xOZ的两条边上）.因此，OC2是两个最大距离OC1、C1C2之和，即OC2的最大值为

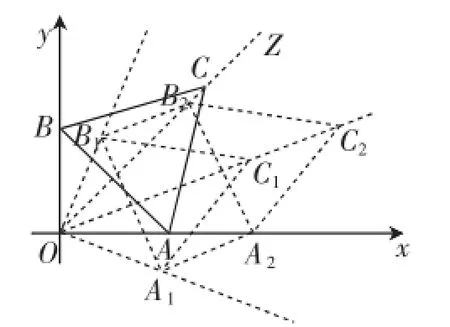
图4

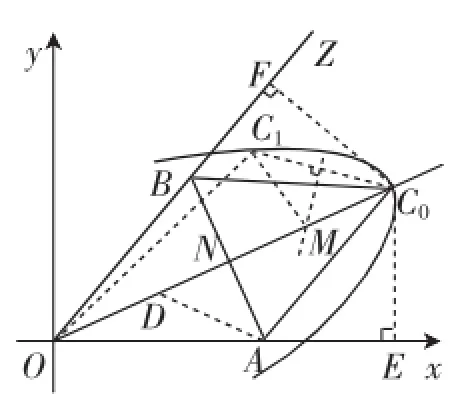
图5

（3）在（1）、（2）中，求上述填空题中OC的最大值时，都是在类比上述那道引例的基础上，经过一番周折做出的.那么，能否通过直接考查填空题中点C的移动轨迹，求得OC的长的最大值呢？

根据图1中正△ABC的移动规律易知，其顶点C的轨迹是一条以射线OC0为对称轴的曲线段（记为“L”，如图5），则C0O的长即为OC的最大值.理由如下：在曲线段L上任取一点C1，并连接C1O、C1C0，根据曲线段L的形状，C1C0的垂直平分线必与C0O相交（记交点为M），根据垂直平分线的性质，则C0O=OM+ MC0=OM+MC1≥OC1，根据点C1的任意性，知C0O最大.另一方面，作C0E⊥x轴，C0F⊥OZ，垂足分别为E、F，则易知△AC0E≌△BC0F，易得∠C0AO=∠C0BO，又因∠C0OA=∠C0OB，AC0=BC0，故△BC0O≌△AC0O，从而AO=BO.因此，OC0垂直平分线段AB，再由∠xOZ=45°，知∠OAB=则

由上述解法可得到以下数学模型：对于等腰△ABC（AC=BC）来说，如果让其底边AB的两个端点A、B分别在定角α的两边上滑动，那么当AB垂直于定角α的平分线时，点C到定角α的顶点的距离最大.

以上数学模型能否再拓展呢？这有必要进一步探究.

2.从反面探究

（1）先给出一个引理，再对所述的填空题进行探究.

引理：如图6，P是⊙O外一点，直线PO分别交⊙O于点A、B，则PA是点P到⊙O上的点的最小距离，PB是点P到⊙O上的点的最大距离.

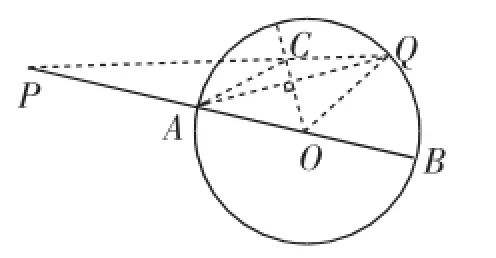
图6

图7

证明：如图6所示，在⊙O上任取一点Q，连接PQ、AQ、OQ，过圆心O向AQ作垂线，交PQ于点C，再连接AC，由垂径定理及线段垂直平分线的性质，知AC=QC.则PB= PO+OB=PO+OQ≥PQ=PC+CQ=PC+CA≥PA.这表明PA是最小距离，PB是最大距离.

（2）在图1中，考虑到在△ABC与∠xOZ中，虽然一个在“动”，一个是“静”，但其位置关系具有相对性，不妨反过来思考，假设△ABC的位置不变，而使∠xOZ的位置变化.因为∠xOZ=45°，AB=2，所以在∠xOZ的位置变动过程中，点O移动的路径应是以AB为弦、内接角为45°的圆弧AB（见图7中⊙O1的实线部分）.此时，作射线CO1，交弧AB于点O，根据引理，CO就是所求的最大距离（此时平面直角坐标系xOy所在的位置如图7所示）.

再计算CO的长度.连接AO1、BO1，根据垂直平分线的判定定理，由AO1=BO1，AC=BC，知射线CO1垂直平分AB，再根据等腰三角形的“三线合一”性质，OC平分∠AO1B，故由圆心角与圆周角的关系知∠AO1E=∠AOB=45°，得

三、拓展延伸

仅考查点C与点O不在直线AB同侧的情况，而对于点C与点O在直线AB同侧的情况，可仿此进行探究.

（1）首先约定：①只改变填空题中△ABC的形状，并令∠xOZ=α，∠ABC=β，AB=c，BC=a，BC≥AC，其他条件不变.②把以AB为弦，其内接角为α的圆弧称为“弧AB”，它是⊙O1的实线部分.③在下列各图中，平面直角坐标系xOy（一般不再画出来）所在的位置均按以下方法确定，“以点O为原点，射线OA为x轴的正半轴，射线OB（即OZ）位于第一象限内（当α<90°时）或第二象限内（当180°>α> 90°时）”，也可能与y轴重合（当α=90°时）.

（2）以下分四种情况讨论，且每种情况下均假设△ABC的位置不变，仅使∠xOZ的位置发生变化，因此点O的移动路径均为以AB为弦，其内接角为α的圆弧.

①当点C在⊙O1外部，而圆心O1在∠C内部时（见图8），作射线CO1，交弧AB于点O，根据引理，CO就是所求的最大距离.而由BC≥AC，知边CA的长即是点C到弧AB的最小距离（可参考引理的证法来证），过点C作CF⊥AB，垂足为F，根据勾股定理，得：

图8

再计算OC的长度：连接AE，则∠BAE=∠AEC-∠ABC=∠AOB-∠ABC=α-β.再连接AO1、BO1、EO1，并作O1M⊥AB，垂足为M，O1N⊥BE，垂足为N，易知BO1=因此，再由勾股定理得：

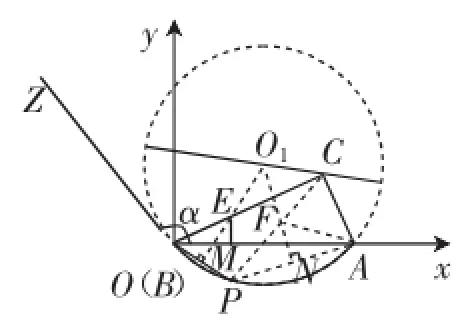
图9

图10

②当点C不在⊙O1外部，而圆心O1不在∠C内部时（见图9），由于直线CO1与弧AB没有交点，所以由BC≥AC，知点C到弧AB的最大距离应为BC=a（此时，点O与点B重合，且∠xOZ=∠APO），点C到弧AB的最小距离应为CA的长.

③当点C不在⊙O1外部，而圆心O1在∠C内部时（见图10），在弧AB任取一点P，分别连接O1P、CP，则OC= O1O+O1C=O1P+O1C≥CP，这表明OC就是所求的最大距离.

再计算OC的长度：延长BC交⊙O1于点E，连接AE，则∠BAE=（180°-∠AEB）-∠ABC=α-β.以下与①同法可得：OC=

图11

④当点C在⊙O1外部，而圆心O1不在∠C内部时（见图11），由于射线CO1与弧AB交于点O和点D，根据引理，CO就是所求的最大距离，CD是点C到弧AB的最小距离.

计算OC、CD长度时，与①中的方法类似，故同理可得：

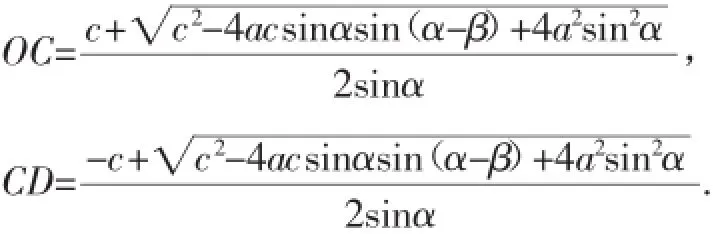
至此又可得到以下数学模型：对于任意△ABC（不妨令AC≥BC）来说，如果让其一边AB的两个端点A、B分别在定角α的两边上滑动（设以AB为弦，其内接角为α的圆弧称为“弧AB”，“弧AB”的圆心为O1，作射线CO1交“弧AB”于点O），那么在边AB滑动过程中，点C到定角α的顶点的最大距离是CO（或CA）.

四、几点感悟

（1）对于本文所述的填空题来说，以上的各种解法及变式，并不一定要一股脑儿地用在教学中，而应视情况来选用（例如：当学习几何变换的用法时，可选用从正面探究的（2）的做法；当学习圆的相关知识时，可选用从反面探究的（2）的做法；当上专题探究课时，则以上的各种解法及变式均可选用）.但以上的探究却是十分必要的，这是因为解题研究是搞好解题教学的前提，为了教会学生解题，教师首先要研究如何解题，善于一题多解、一题多变，这样的探究越是有深度，就越有利于把数学问题开发成更优质的教学资源，更好地提升其应用价值.

（2）对于动态型几何题来说，“动”与“静”是相对而言的，它们既互相对立，又能相互转化，但“动”应该成为关注的焦点.而对于图形的“动”，要善于从数形结合的角度，仔细考查“动”的路径及其所达到的关键位置、“动”所引发的数量关系的变化情况等要素，以把握问题内在的深层联系，并通过联想相关的知识，找出有效的解题方法.如在图1中，通过考查△ABC的运动，求OC的最大值就比较困难，而根据“正难则反，逆向探索”的策略，引导学生换一种角度进行思考，使△ABC的位置保持不变，反过来考查∠xOZ的运动，不仅容易求出OC的最大值，而且便于进一步推广.

（3）在解答完一个问题后，为了把学生的思维引向深入，实现从解题到研题的升华，就要善于启发学生对解题过程进行反思，看看该过程是否可以优化，解答中用到了哪些数学思想，还有没有更好的解题方法，所用的解题方法能否进行推广等.这样的反思活动，既有利于学生养成良好的数学学习习惯，也有助于他们积累数学活动的经验，使其真正学会分析问题、解决数学问题的方法，优化学生的思维品质，提高学生的数学素养.

1.朱玉祥.一道填空题的高零分率引发的思考［J］.中学数学教学参考（中），2014（4）.H