重视教材“探究活动”,专业自主增设课时
——李庾南老师“平行线分线段成比例”课例赏析
重视教材“探究活动”,专业自主增设课时
——李庾南老师“平行线分线段成比例”课例赏析
☉江苏省如皋经济技术开发区袁桥初中 谢裕宏
最近,笔者有机会观摩学习了著名特级教师李庾南老师的一节“平行线分线段成比例定理”公开课教学,由于该课的教学内容在当前一些九年级数学教材中被弱化为一个“探究活动”,并且没有要求学生给出具体的证明过程,然后作为所谓的“基本事实”让学生可以直接使用,用于相似三角形的性质后续推证.然而,从几何学习的逻辑连贯、前后一致的高度出发,平行线分线段成比例定理作为一个单独的教学课时显然有着十分重要的价值,本文整理该课的教学流程,分享并赏析专家教学的实践智慧.
一、“平行线分线段成比例定理”教学流程
1.开课阶段
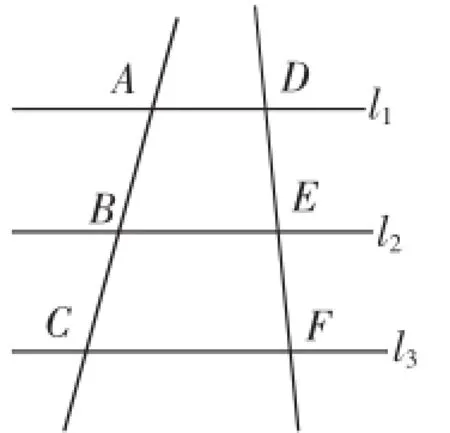
图1
提出问题:平行线分得的对应线段的比k=1推广到一般正实数k值.
2.新知探索
师生共同探讨转化方法:你准备通过什么途径得到“一组平行线在两条直线上截得的对应线段成比例”?引导学生先将问题“数学化”,如图2

图2

图3
师生合作“转化”,从最简单的情况出发,如图3,
若AB=2BC时,如何转化,才能证得结论?以B为起点,在BA上顺次截取和BC相等的线段,2次正好截尽,截点为M、A,过点M作l∥l1交DF于点N,根据平行线等分线段定理=2,即l1//l2//l3⇒所以,以B为起点,在BA上顺次截取和BC相等的线段,n次后正好截尽时,就可以转化为“平行线等分线段”,因而结论成立.

图4
若截不尽呢?如图4,截两次后,剩余一条小于BC的线段PA时,能不能化为“平行线等分线段”呢?请你将自己的研究结果讲给同学们听.
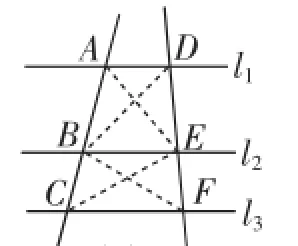
图5
预设另外的证明思路:“面积法”.如图5,根据“同底同高的三角形等积”,可得S△ABD= S△AED,S△BCE=S△BFE.根据“同高的三角形面积的比等于底的比”,可得
概括性质:三条平行线截两条直线,所得的对应线段成比例.
3.变式思考
变式思考1:比如进一步研究被三条平行线所截的两条直线的位置情况,可分为两类:如图6,l1//l2//l3,截AC、DF,AC//DF;如图7,l1//l2//l3,截AC、DF,AC与DF相交.

图6

图7
变式思考2:再研究被三条平行线所截的两条相交直线的交点与平行线的位置情况,你认为有几种情形?请你画出相应的图形(如图8、图9、图10),根据图形用符号语言表达“平行线分线段成比例定理”的内容.

图10
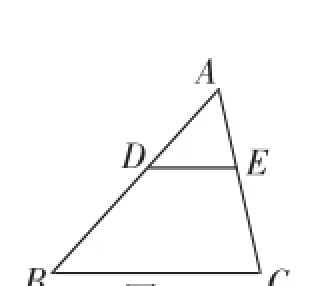
图11
图8

图9
变式思考3:请同学们观察图11,研究:把定理运用于△ABC中,能得到怎样的推论?
在△ABC中,DE//BC交AB于点D,交AC于点E,则
推论:平行于三角形一边的直线截其他两边(或其延长线),所得对应线段成比例.
4.课堂小结
教师结合PPT展示本课内容的知识结构,如图12所示.
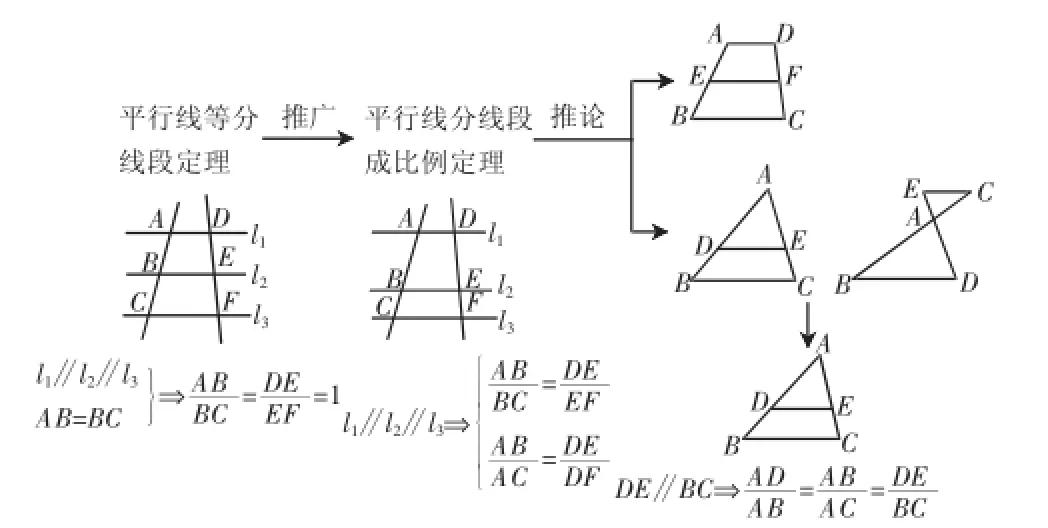
图12
5.布置课外作业
(1)反思、总结课堂研究方法和内容,掌握平行线分线段成比例定理及其推论.
(2)书面作业.
证明:①平行于三角形一边并且和其他两边相交的直线,所截得的三角形的三边与原三角形的三边对应成比例;
②平行于三角形一边并且和其他两边的反向延长线相交的直线,所截得的三角形的三边与原三角形的三边对应成比例.
二、课例赏析
1.追求逻辑连贯、前后一致的几何教学
近一段时间,人教社中数室资深编审章建跃博士倡导“逻辑连贯、前后一致”的数学教学得到一线教师的共鸣和热议.从李庾南老师上述课例能看出,她正是基于构建前后一致的几何教学的认识高度下,预设了平行线分线段成比例定理的教学,有这样一节课,就使得后续相似三角形的判定、性质都找到了知识生长点,新知的产生自然而和谐,也使得所谓的“基本事实”成为可以追问和证明的命题,提高了学生对几何知识、逻辑证明的可信度.
2.启发教师从“教教材”到“用教材教”
华东师大钟启泉教授曾指出:“在‘教教材’的场合下,教师回避了教育研究的根本问题——为什么教、教什么,教师的责任就是如何把教科书提供的教材经过自身咀嚼之后再喂给学生.这是一种‘告知式’的技术主义的教学方法,反映了‘教科书中心主义’的教育观.”如上文课例所见,当我们实践者面对教材上某一个“探究活动”,如果基于“理解数学”的高度感觉确有拓展研究的需要,则要大胆预设,增加新授课时,从“教教材”走向“用教材”,让学生理解数学、理解几何、理解数学的“一步一步向上走”.
1.李庾南.自学·议论·引导教学论[M].北京:人民教育出版社,2013.
2.章建跃,陈向兰.数学教育之取势明道优术[J].数学通报,2014(10).
3.钟启泉.新旧教学的分水岭[J].基础教育课程(上),2014(2).
4.章建跃.构建逻辑连贯的学习过程使学生学会思考[J].数学通报,2013(6).
5.李庾南,陈育彬.中学数学新课程教学设计30例——学力是这样发展的[M].北京:人民教育出版社,2007.H

