基于鲁棒UKF 的永磁同步电机转子速度估计

沈绍博，祖 晖，李 涛，，费树岷

(1.南京航空航天大学自动化学院，南京210016;2.张家港智能电力研究院智电柔性输配电技术研究所，江苏张家港215600;3.东南大学自动化学院，南京210096)

0 引言

直驱永磁同步电机(DD-PMSG:Direct-Driven Permanent Magnetic Synchronous Generator)具有结构简单、发电效率较高且运行可靠性好等优点，已成为现代大型变速恒频风电机组主要的发展方向之一［1］。直驱永磁同步电机转速控制需要对发电机转速进行测量，而大型风力发电系统的发电机往往位于远离地面的塔架顶端，使用测速传感器不利于机组的维护和检修，所以有些学者开始关注通过其他手段估计转速和位置的方法［2-6］。

传统的基于系统模型方法大多采取扩展卡尔曼滤波(EKF:Extended Kalman Filtering)方法。如文献［6］通过降低Kalman滤波器阶次减少计算量。文献［7］提出抗差扩展卡尔曼滤波的估计方法，提高了滤波器抗干扰能力。但永磁同步电机模型是一类非线性较强的系统，EKF方法会存在线性化误差。无迹Kalman滤波(UKF:Unscented Kalman Filter)方法基于UT变换，通过一组确定的采样点近似概率密度函数，而不是对非线性函数进行近似，所以得到了许多学者的关注［8，9］。文献［10，11］将UKF方法运用于永磁同步电机上，取得了较好的效果。但滤波器在迭代过程中可能会产生负定的协方差矩阵，从而使滤波器发散。文献［12］引入平方根UKF方法，解决了滤波过程中协方差矩阵可能不正定的问题。UKF能有效抑制高斯噪声，但对非高斯噪声鲁棒性较差。文献［13］将负载转矩作为变量进行估计，提高了估计精度。文献［14］采用强跟踪滤波原理对平方根UKF进行改进，提高了算法的收敛速度和稳定性。但这两种算法并没有考虑实际工程的应用中永磁同步电机参数会随着工作环境的改变而发生变化、进而影响滤波器估计准确性的问题［15］。

笔者针对具有参数不确定的无位置传感器DD-PMSG系统，将模型转化为由发电机机电状态与定子参数组成的增广系统方程的形式，通过对该增广模型应用一种新颖的鲁棒UKF方法(RUKF:Robust Unscented Kalman Filter)，可同时辨识发电机的机电状态和定子不确定参数动态。与传统UKF方法的仿真实验对比结果表明，该方法对具有不确定性及非高斯噪声的系统模型有较强的鲁棒性。

1 DD-PMSG旋转坐标系下的摄动模型

PMSG在旋转坐标系下的微分方程如下

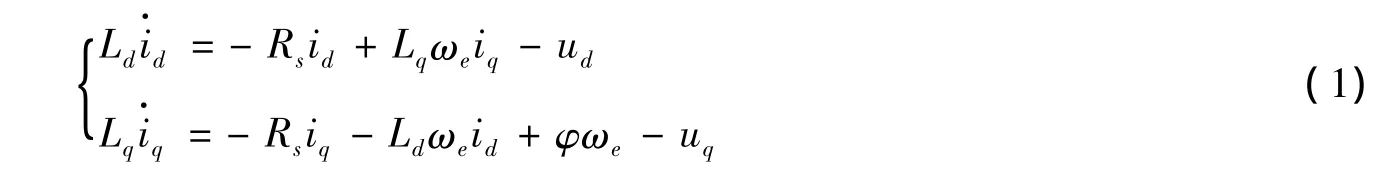
其中ud和uq是d、q轴电压分量;id和iq是d、q轴电流分量;Ld和Lq是d、q轴等效电感。ωe是电角速度;φ是永磁体磁链。由于建模存在误差，所以将系统(1)改写为变参数并具有建模误差的形式，即

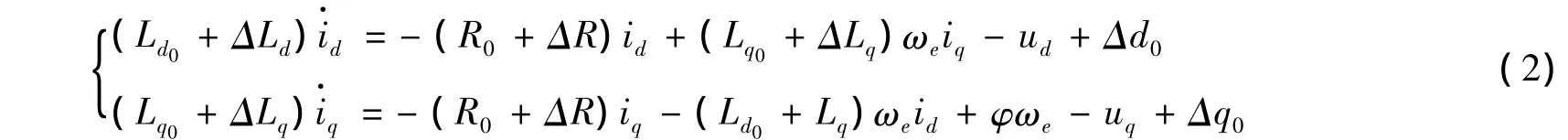
其中Δd0和Δq0是系统未建模动态;将式(2)两端分别除以Ld0、Lq0，并分别将(1+ΔLd/Ld0)－1和(1+ΔLq/Lq0)－1进行一阶 Taylor展开，整理可得

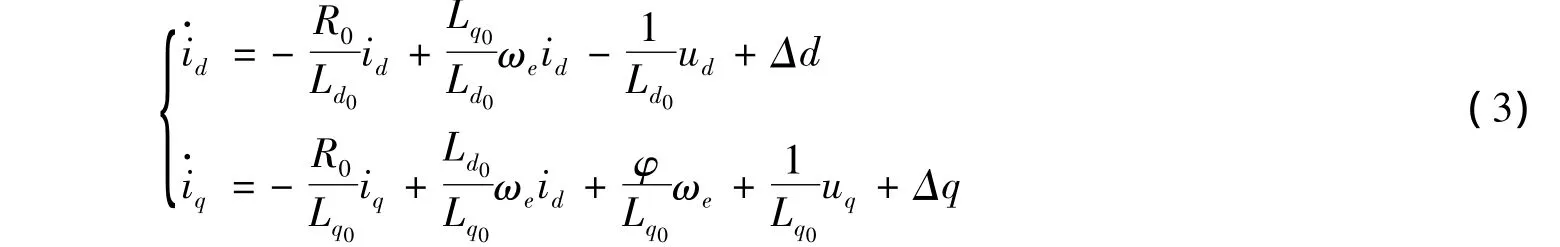
由于机械转速变化过程的时间常数一般远大于电磁过程的时间常数，因此，可认为在电参数的采样期间转子角加速度在0附近变化，即有

尽管id，iq不能直接测得，但可通过将a－b－c坐标系下测得的三相电流旋转变换得到，因此，可将定子电流id，iq作为测量值。综合式(3)与式(4)可建立下面的三阶模型

对系统(5)进行离散化，建立PMSG的离散时间模型

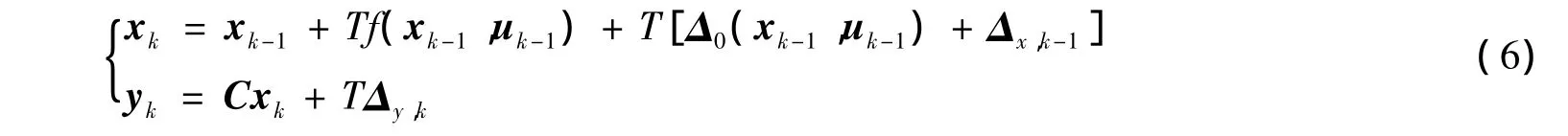
2 基于鲁棒平方根UKF方法的PMSG转速估计

笔者将利用鲁棒平方根UKF方法，对系统(6)的增广模型进行带参数估计的速度鲁棒估计。对该增广模型运用滤波算法，可达到对转速和不确定参数同时进行估计，从而提高估计精度和不确定参数的鲁棒性。

2.1 鲁棒平方根UKF方法

由于UKF以UT变换为基础，采用卡尔曼线性滤波框架，通过一组确定的采样点近似概率密度函数，而不是对非线性函数进行近似。在实际应用中，由于在数值计算中往往存在舍入误差，有时会得到负定的协方差矩阵，从而导致UKF滤波器无法工作。平方根UKF算法用协方差平方根代替协方差参加递推运算，可以保证滤波算法的数值稳定性。

鉴于系统(6)满足如下非线性系统状态方程和测量方程

其中f(·)和h(·)分别是系统状态的输入和噪声的连续可微函数向量，过程噪声{ωk}与测量噪声{vk}为相互独立的高斯过程噪声，其协方差阵分别为Qk，Rk。

平方根UKF算法如下［16］。

1)初始化。

2)选取2n+1个采样点。

其中L=n为状态个数，λ通常取0或n－3。

3)时间更新。

4)测量更新。

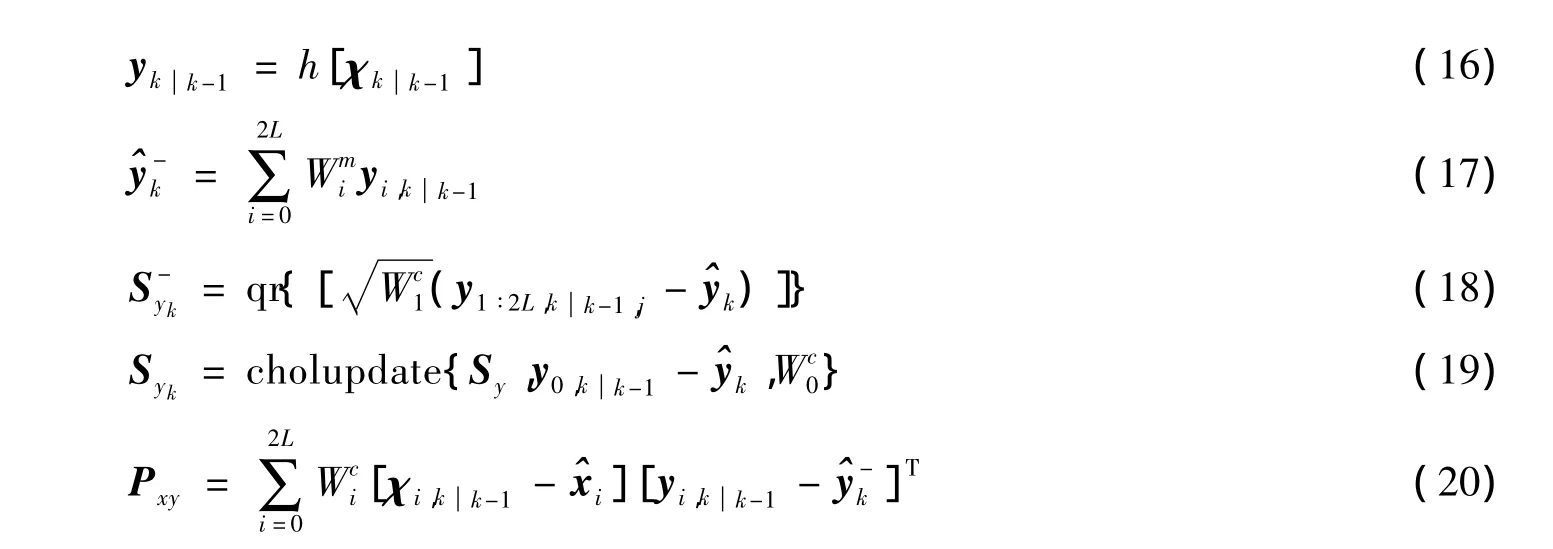
滤波器消除测量误差的过程实质上是通过比较协方差矩阵的理论值与真实值实现的，当测量系统存在故障时，得到的错误测量值会使滤波器产生错误的估计输出。为确保滤波器的鲁棒性，增加了鲁棒性因子矩阵Ak，以调节协方差的真实值与估计值［17］，分别如下

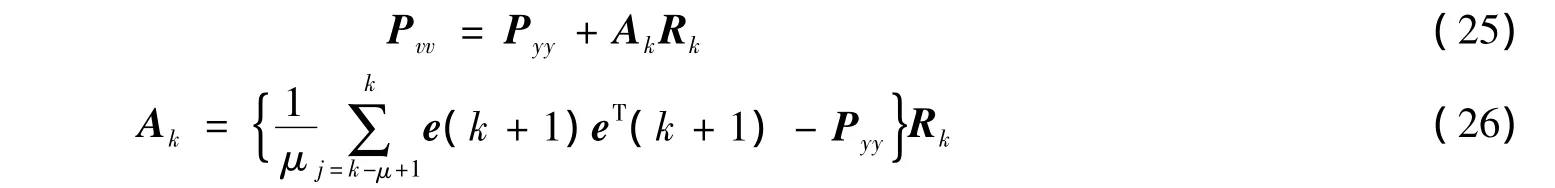
其中 ai=max{1，Ak(i，i)}，i=1，2，…，n。

则滤波器的卡尔曼增益变为

只有当测量系统得到的测量值不准确时，鲁棒算法才会对滤波器参数产生影响。系统正常运作时，Ak=I(I为适当维数的单位阵)，滤波器等同于UKF。而当测量发生故障时，协方差矩阵中Ak值增大，从而增大协方差矩阵P并减小卡尔曼滤波增益K。错误测量值会被视为具有较小的权值，使滤波器输出的估计值产生较小的变化［18］。即消除了错误测量值的影响，从而提高系统鲁棒性。

2.2 带参数估计的滤波模型

针对系统(6)，状态向量xk与不确定参数有关，令δ=［ΔRsΔLqΔLd］T，则状态变量都是δ的函数，所以系统(6)可重新表示为

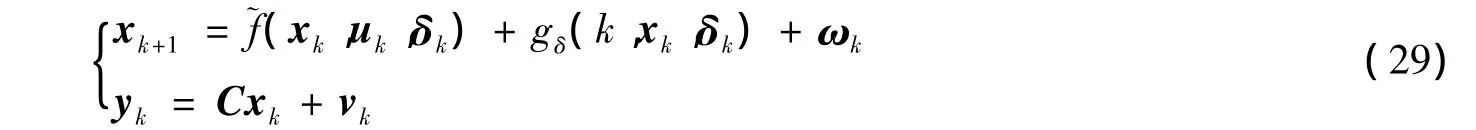
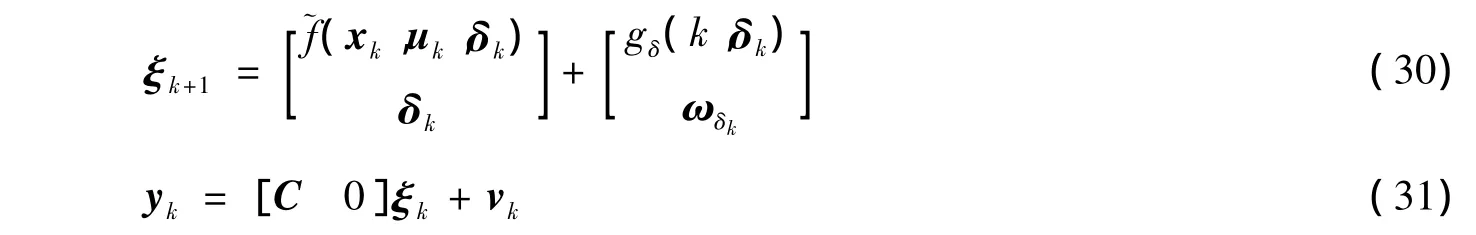
通过带参数估计的滤波方法，将模型转化为由发电机机电状态和定子参数组成的增广系统方程的形式。对该增广系统采用鲁棒平方根UKF方法，使定子参数也参与到发电机状态的迭代过程中，可同时辨识发电机的机电状态和定子不确定参数动态。上一时刻的估计参数参与到下一时刻的状态估计，以增加系统维数为代价提高了系统对不确定参数的鲁棒性。

3 仿真实验

无速度传感器DD-PMSG估计系统的结构如图1所示，其中MPPT(Maximum Power Point Tracking)为最大风能捕获模块，SVPWM(Space Vector Pulse Width Modulation)为空间矢量脉宽调制。实验中电机参数如表1所示，滤波器参数选定为

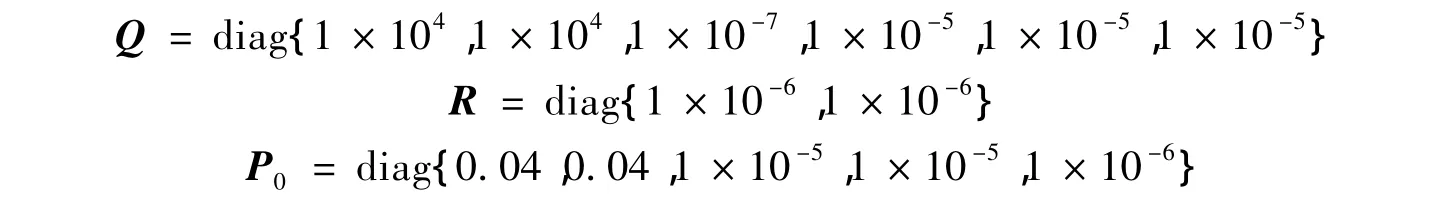
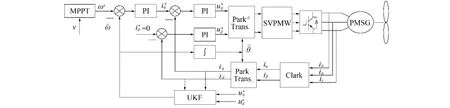
图1 控制框图Fig.1 Control scheme

表1 电动机参数Tab.1 The motor parameters

笔者通过4个仿真实验比较传统平方根UKF和鲁棒UKF方法的性能。

实验1 系统工作在正常情况下，测量噪声为高斯噪声。两种估计方法转速误差的仿真结果如图2所示。可见，在系统正常运转时，鲁棒UKF方法等同于UKF方法，无明显差别。两种方法转速误差的不同主要是由测量噪声随机性所引起的。

实验2 测量时存在高斯噪声，假设在2 s时系统测量值有误:给id测量值叠加一个当前值10%的脉冲信号，转速误差的仿真结果如图3所示。结果表明，在测量值产生突变后，传统UKF方法对非高斯噪声已经不适用，而笔者方法则可通过减小卡尔曼滤波增益消除测量故障的影响。

实验3 在实际系统中，电感参数通常具有较强的不确定性。在无测量噪声的情况下，使算法运行过程中，电感实际值与标称值相比有1 mH变化，用来验证系统对参数不确定性的鲁棒性，其结果如图4所示。

由于ΔLd以及ΔLq与Δd和Δq的倒数关系，电感的微小变化对这两项的影响会造成较大的模型参数误差。从图3中可以看出，由于电感参数偏离实际值，UKF的估计误差不断增大，估计值不断偏离实际值。而带参数估计的RUKF方法，由于定子不确定参数参与到迭代过程中，所以滤波器能准确估计出转速。图3仿真结果显示出RUKF方法对电感不确定具有较强的鲁棒性。

实验4 在具有高斯测量噪声的情况下，假设电感实际值减小1 mH，并在2 s时给id测量值叠加一个当前值10%的脉冲信号，检验滤波器在综合环境下的性能。两种方法的转速估计误差如图5所示。

由于电感参数不确定的影响，传统UKF方法在开始估计时逐渐偏离真实值，在2 s时测量值产生突变后，传统UKF方法无法收敛到正确的估计值。而RUKF方法虽然在参数不确定和测量值不准确的情况下产生偏差，但仍能较准确估计出转速，鲁棒性能明显优于传统UKF方法。

图2 高斯噪声对转速估计影响Fig.2 Impact of Gaussian noise

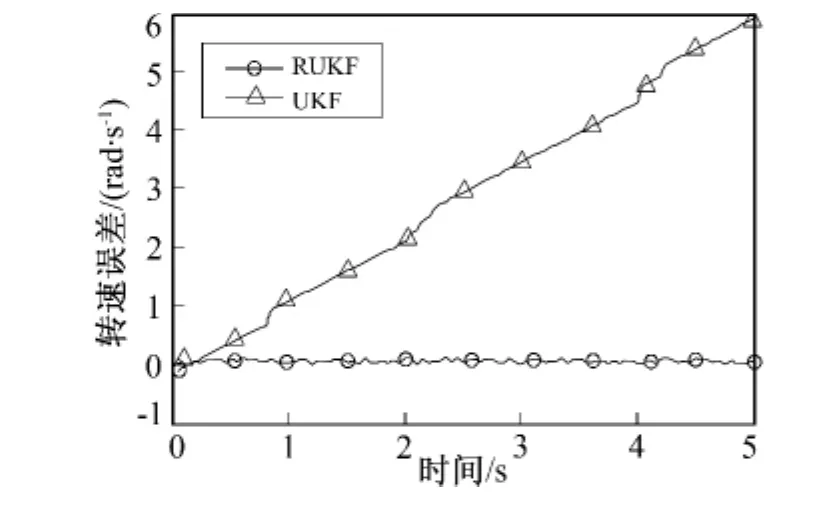
图4 对电感参数变化的鲁棒性Fig.4 Robustness to the variation of Inductance parameter

图3 脉冲信号对转速估计影响Fig.3 Impact of the pulse signal

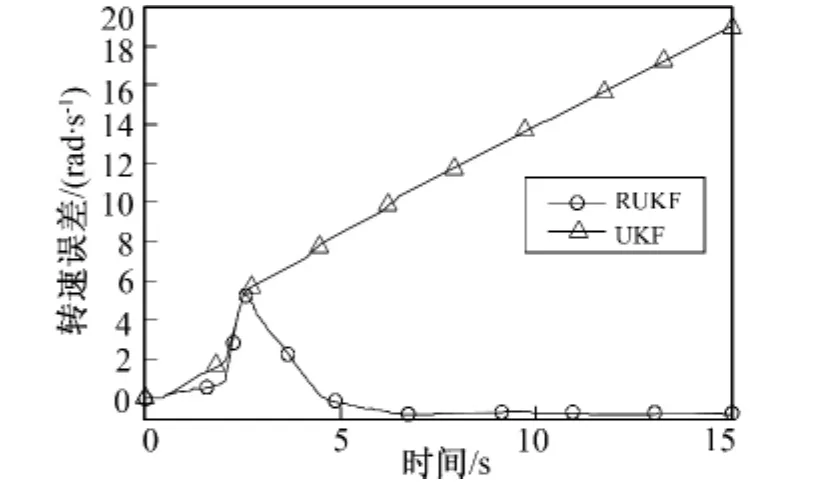
图5 滤波器转速估计综合性能Fig 5 Comprehensive performance of speed estimation

4 结语

在平方根无迹Kalman滤波的基础上，笔者将鲁棒平方根UKF方法运用到直驱永磁同步电机的转速估计中，并将不确定参数引入增广向量，通过估计参数和估计状态之间的相互更新，提高滤波器对非高斯噪声及参数不确定性的鲁棒性。仿真结果表明，该方法对具有参数不确定性与测量噪声的系统，在鲁棒性能上较传统平方根UKF方法有明显提升。另外，UKF方法除了可用于永磁同步电机状态估计，也可对电机参数进行估计［20］，带参数估计的RUKF的设计思想同样适用于其他具有此类非线性动态特征的系统，具有一定的理论价值和应用前景。

［1］ACCETTA A，CIRRINCIONE M，PUCCI M，et al.Sensorless Control of PMSM Fractional Horsepower Drives by Signal Injection and Neural Adaptive-Band Filtering［J］.IEEE Transactions on Industrial Electronics，2012，59(3):1355-1366.

［2］齐冀龙，田彦涛，龚依民，等.无传感器PMSM直接计算与自适应算法［J］.吉林大学学报:信息科学版，2009，27(1):23-30.

QI Jilong，TIAN Yantao，GONG Yimin，et al.Algorithms of Sensorless PMSM Control System Based on Direct Computation and Model Reference Adaptive System［J］.Journal of Jilin University:Information Science Edition，2009，27(1):23-30.

［3］BOLOGNANI S，CALLIGARO S，PETRELLA R，et al.Sensorless Control of IPM Motors in the Low-Speed Range and at Standstill by HF Injection and DFT Processing［J］.IEEE Transactions on Industry Applications，2011，47(1):96-104.

［4］王高林，杨荣峰，李刚，等.基于高频信号注入的IPMSM无位置传感器控制策略［J］.电工技术学报，2012，27(11):62-68.

WANG Gaolin，YANG Rongfeng，LI Gang，et al.Position Sensorless Control Strategy of IPMSM Based on High Frequency Signal Injection［J］.Transactions of China Electrotechnical Society，2012，27(11):62-68.

［5］徐鹏，肖建，杨奕，等.永磁同步电机双率残差增广最小二乘参数辨识［J］.电机与控制学报，2014，18(4):45-51.

XU Peng，XIAO Jian，YANG Yi，et al.Residual Based Extended Least Squares Identification Method of Permanent Magnet Synchronous Motor Dual-Rate Sampling Data System ［J］.Electric Machines and Control，2014，18(4):45-51.

［6］李旭春，张朋鸟，赵非，等.改进EKF的异步电机无速度传感器矢量控制［J］.电机与控制学报，2013，17(9):24-29.

LI Xuchun，ZHANG Pengniao，ZHAO Fei，et al.Improving Speed Sensorless Extended Kalman Filter for Vector Control of Induction Motor［J］.Electric Machines and Control，2013，17(9):24-29.

［7］尹忠刚，张瑞峰，钟彦儒，等.基于抗差扩展卡尔曼滤波器的永磁同步电机转速估计策略［J］.控制理论与应用，2012，29(7):921-927.

YIN Zhonggang，ZHANG Ruifeng，ZHONG Yanru，et al.Speed Estimation for Permanent Magnet Synchronous Motor Based on Robust Extended Kalman Filter［J］.Journal of Control Theory and Applications，2012，29(7):921-927.

［8］XIONG K，WEI C L，LIU L D.Robust Unscented Kalman Filtering for Nonlinear Uncertain Systems［J］.Asian Journal of Control，2010，12(3):426-433.

［9］LI Wenling，JIA Yingmin.H-Infinity Filtering for a Class of Nonlinear Discrete-Time Systems Based on Unscented Transform［J］.Signal Processing，2010，90(12):3301-3307.

［10］余佩琼，王涌，杨伟民，等.UKF在永磁同步电机无位置传感器控制中的应用［J］.机械工程学报，2007，43(11):149-153.

YU Peiqiong，WANG Yong，YANG Weimin，et al.Applications of Unscented Kalman Filter on Position Sensorless Control of Permanent Magnet Liner Synchronous Motor［J］.Chinese Journal of Mechanical Engineering，2007，43(11):149-153.

［11］MOON C，NAM K H，JUNG M K，et al.Sensorless Speed Control of Permanent Magnet Synchronous Motor Using Unscented Kalman Filter［C］∥SICE Annual Conference(SICE).Akita:IEEE，2012:2018-2023.

［12］曲智勇，姚郁，韩俊伟.基于改进型平方根UKF算法的永磁同步电机状态估计［J］.电机与控制学报，2009，13(3):452-457.

QU Zhiyong，YAO Yu，HAN Junwei.State Estimanon of Permanent Magnet Synchronous Motor Using Modified Square Root UKF Algorithm ［J］.Electric Machines and Control，2009，13(3):452-457.

［13］JANISZEWSKI D.Load Torque Estimation in Sensorless Pmsm Drive Using Unscented Kalmana Filter［C］∥Industrial Electronics(ISIE)，2011 IEEE International Symposium on.Gdansk:IEEE，2011:643-648.

［14］许波，朱幌秋，姬伟，等.改进型平方根无迹卡尔曼滤波及其在无轴承永磁同步电机无速度传感器运行中的应用［J］.控制理论与应用，2012，29(1):53-58.

XU Bo，ZHU Huangqiu，JI Wei，et al.Modified Square-Root Unscented Kalman Filter and Its Application to Speed Sensorless Control of Bearingless Permanent Magnet Synchronous Motor［J］.Journal of Control Theory and Applications，2012，29(1):53-58.

［15］BARUT M，BOGOSYAN S，GOKASAN M.Experimental Evaluation of Braided EKF for Sensorless Control of Induction Motors［J］.IEEE Transactions on Industrial Electronics，2008，55(2):620-632.

［16］卫志农，孙国强，庞博.无迹卡尔曼滤波及其平方根形式在电力系统动态状态估计中的应用［J］.中国电机工程学报，2011，31(16):74-80.

WEI Zhinong，SUN Guoqiang，PANG Bo.Application of UKF and SRUKF to Power System Dynamic State Estimation ［J］.Proceedings of the CSEE，2011，31(16):74-80.

［17］HALIL ERSIN SOKEN，CHINGIZ HAJIYEVB，SHIN-ICHIRO SALCAI.Robust Kalman Filtering for Small Satellite Attitude Estimation in The Presence of Measurement Faults［J］.European Journal of Control，2014，20(2):64-72.

［18］HALIL ERSIN SOKEN，CHINGIZ HAJIYEVB.Pico Satellite Attitude Estimation via Robust Unscented Kalman Filter in the Presence of Measurement Faults［J］.ISA Transactions，2010，49(3):249-256.

［19］祖晖，沈绍博，李涛.基于扩展H∞滤波方法的无位置传感器DD-PMSG的转子位置和速度鲁棒估计［C］∥中国制导、导航与控制学术会议.烟台:IEEE，2014:1325-1330.

ZU Hui，SHNE Shaobo，LI Tao.Speed and Rotor Position Estimation for Sensorless DD-PMSM Based on Extended H∞Filtering［C］∥IEEE Conference on CGNCC.Yantai，China:IEEE，2014:1325-1330.

［20］VEPA R.Nonlinear，Optimal Control of a Wind Turbine Generator［J］.IEEE Transactions on Energy Conversion，2011，26(2):468-478.