煤矿井下救援定位系统研究

郭继坤，马鹏飞，赵肖东

(黑龙江科技大学电气与控制工程学院，哈尔滨150022)

0 引言

目前，煤矿井下监控、人员定位和通信系统采用有源通信方式。这种通信方式存在的问题是当井下发生爆炸或透水等事故时，通信系统会遭到破坏。即使不被破坏，也将所有传输线路的电源切断，以防止线路产生电火花引起新的灾难。从而给救援工作带来很大的困难。

针对以上问题，笔者设计了基于双Mach-Zehnder干涉仪结构的矿井下救援定位系统，其位于井下部分的设施全部无源，无需供电。考虑灾情发生时，光纤被毁、折断的可能性较大，因此将光缆埋在煤矿井下巷道下面，以确保系统更加安全、可靠。当发生矿难井下通信系统中断时，被困人员可挖开巷道，直接触及附近光缆产生振动信号，通过对此振动信号进行处理、分析，获取井下人员的位置信息［1-3］。为了提高定位精度，笔者同时提出了一种基于小波阈值降噪的互相关时延估计算法，并对该算法进行了仿真验证。

1 系统结构及原理

系统结构如图1所示。布设在井下光缆中的3条单模光纤构成了双Mach-Zehnder干涉仪的分布式光纤振动传感器，用于获取人员敲击的振动信号，其中两条单模光纤用于构成传感器的两个传感臂，第3条单模光纤用于信号的传输。

图1 系统结构Fig.1 System architecture

系统定位原理如图2所示。光源发出的光经耦合器C1后被分为两束，井下传感光缆检测到被困人员敲击的振动信号后，沿方向1传播的光波经耦合器C3分光后在耦合器C4处发生干涉，干涉信号经信号传输光纤F3达到耦合器C5，探测器D2检测到此干涉信号y1(t)。同理，探测器D1可检测到沿方向2传播的光波在耦合器C3处所发生干涉的干涉信号y2(t)。通过测定这两路干涉信号到达探测器D2和探测器D1的时间差即可实现定位。定位公式为［2］

图2 系统定位原理图Fig.2 Schematics of system positioning

其中c为光在真空中传播速度，n为单模光纤折射率，Δ τ为信号y1(t)和信号y2(t)分别到达探测器D2和探测器D1的时间差。由式(1)可知，n、c为已知量，只需测得接收信号y1(t)与y2(t)之间的时间差Δ τ，即可获得求救人员位置x。目前，互相关算法以其运算量小、容易实现等优点成为Δ τ求取的最常用算法［4］。

2 直接互相关时延估计算法

直接互相关时延估计算法先求信号y1(t)与y2(t)的互相关函数

设n1(t)与n2(t)为噪声，则两个探测器的实际输出信号可表示为［2］

令 s(t)=I1{1+cos［φ0+(1－K)Δ φ(t－τ1)］}，则式(3)、式(4)可简化为

其中m=I2/I1。将式(5)和式(6)代入式(2)有

其中Rn1n2(τ)、Rsn2(τ)和Rsn1(τ－Δ τ)分别为噪声与噪声、噪声与振动信号之间的互相关函数。直接互相关求时延的方法:假设 Rn1n2(τ)、Rsn2(τ)和 Rsn1(τ－Δ τ)都为零，则有

由式(8)可知，互相关函数最大值处的τ即为所求的时延Δ τ。然而，实际情况中的噪声与噪声、噪声与振动信号之间不一定完全不相关，即式(7)中的Rn1n2(τ)、Rsn2(τ)和Rsn1(τ－Δ τ)不一定全部为零，使Rxy(τ)的峰值所对应的时间点偏离 Δ τ，导致算法的时延估计性能下降。信号的信噪比越低，Rn1n2(τ)、Rsn2(τ)和 Rsn1(τ－Δ τ)的影响越大，导致最终系统的定位误差越大［1］。因此，提高系统定位精度的关键在于提高信号的信噪比。传统提高信号信噪比的降噪方法为:先对信号进行傅里叶变换，然后采用低通滤波器进行滤波，这种方法不适合于信号和噪声频带相互重叠的情况［5］。如用此方法，需设计一个带通滤波器，对高频与低频的噪声进行去除，然而，当采样率较高时，该设计不仅难以实现而且容易引入误差，使系统定位精度下降［6］。

3 小波降噪互相关时延估计算法

3.1 小波阈值降噪

笔者提出利用小波阈值降噪提高信号的信噪比，其主要的理论依据为:在小波域内，由于信号与噪声的能量分布不同，而且对信号进行小波变换后，其小波的变换系数比噪声的系数大，所以，只要找到一个数作为阈值，当小波的变换系数小于该阈值时，则去除小波系数;当小波的变换系数大于该阈值时，则保留小波系数，以此达到去噪的目的［7］。

假设s(t)为原始信号，n(t)为高斯白噪声，服从N(0，σ2)，则原始信号叠加白噪声后的信号可表示为

对f(t)进行离散小波变换，有

其中 wf(j，k)、ws(j，k)、wn(j，k)分别表示信号 f(t)、s(t)和噪声 n(t)信号在第 j层上的小波系数，J 为小波变换的最大分解层数;N为信号的长度。

小波变换是一个线性变换过程，对信号f(t)进行离散小波变换后的小波系数wf(j，k)由两部分组成:一部分为 ws(j，k)，另一部分为 wn(j，k)［7］，记 wf(j，k)、ws(j，k)、wn(j，k)分别为 wj，k、uj，k、vj，k。首先选取阈值 λ 对 wj，k进行阈值处理，得到阈值处理后的小波系数，使与 uj，k尽量接近，然后对估计的小波系数进行小波重构，得到去噪后信号^s(t)。经过多次的对比计算，笔者最终选择的小波基为sym6，分解层数为5层，阈值通过文献［8］所提出的改进阈值确定方法确定，表示为

3.2 小波阈值降噪互相关时延估计

基于小波阈值降噪的互相关时延估计算法基本思路:先对探测器所接收到的两路信号进行小波阈值降噪，提高信号的信噪比，然后对降噪后的两路接收信号利用互相关算法求取时延［9］。算法具体流程如图3所示。

图3 小波阈值降噪互相关时延估计算法流程Fig.3 Wavelet threshold noise cross-correlation delay estimation algorithm flow

4 仿真分析

笔者通过Matlab对上述两种算法进行了仿真比较，仿真所用源信号表达式为

式(1)中，取n=1.5，c=3.0×108m/s。两路信号的实际时延为0.025 ms。分别对两路仿真源信号叠加信噪比为－5 dB的白噪声，叠加白噪声后的两路接收仿真信号如图4所示。图5为直接对两路接收信号进行互相关运算后的波形图;图6为先对两路接收信号进行小波阈值去噪，然后进行互相关运算的波形图;图7为图5波峰的局部放大;图8为图6波峰的局部放大;图9为两种算法的定位性能比较，结果为仿真实验独立重复100次的平均值。

图5 直接互相关法Fig.5 Direct cross-correlation method

图6 小波阈值互相关法Fig.6 Wavelet threshold correlation method

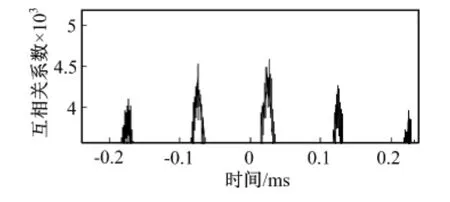
图7 直接互相关法波峰局部放大Fig.7 Direct cross-correlation peaks partial enlarged

图8 小波阈值互相关法波峰局部放大Fig.8 Wavelet thresholding cross-correlation speaks partial enlarged

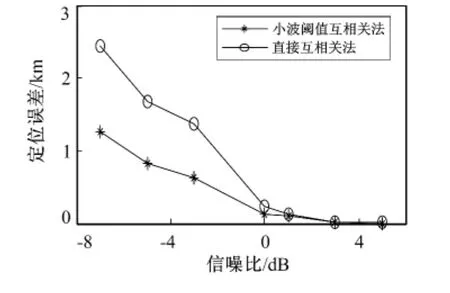
图9 两种算法定位性能比较Fig.9 Positioning performance comparison of two algorithm

由图4可知，由于受到噪声的干扰，两路接收信号无明显的相关性，此时信号的信噪比较低。对此时的两路信号进行直接互相关运算，得到图5所示的互相关波形，其波峰的局部放大如图7所示。由图7可知，互相关波形的波峰不仅产生了明显的伪双相关峰而且波峰值的锐度很差，造成最终的时延估计误差较大，定位精度较低。而图8表明，小波阈值去噪互相关法的互相关波形波峰锐度相对较高，伪双相关峰相对不明显。图9表明，随着信号信噪比的增加，系统的定位精度越来越高，采用小波阈值去噪互相关算法的定位精度高于采用直接互相关算法。

5 结 语

笔者基于双Mach-Zehnder干涉仪结构设计了煤矿井下救援定位系统，解决了矿难发生时无源通信的问题。该系统定位方法容易实现，具有防燃防爆、抗电磁干扰、远程监控等突出优点，具有很大的实际应用价值。针对传统的时延估计算法在忽略噪声影响的条件下性能良好，然而噪声的引入致使传统的时延估计算法性能下降的问题，笔者提出了一种基于小波阈值去噪的互相关时延估计算法。通过仿真分析可知，该算法有效的提高了系统的定位精度，定位性能优于传统互相关时延估计算法。

［1］封皓.基于双Mach-Zehnder干涉仪结构的光纤管道安全预警系统建模及定位研究［D］.天津:天津大学精密仪器与光电子工程学院，2011.

FENG Hao.Study on the Modeling and Location Process of the Distributed Fiber Oil and Gas Pipelines Pre-Warning System Based on Double Mach-Zehnder Interferometer Structure［D］.Tianjin:College of Precision Instrument and Opto-Electronics Engineering，Tianjin University，2011.

［2］潘岳，王健.双马赫-曾德尔型干涉仪定位技术研究［J］.光学仪器，2012，34(3):54-59.

PAN Yue，WANG Jian.Research of Double Mach-Zehnder Interferometer Positioning Technology ［J］.Optical Instruments，2012，34(3):54-59.

［3］张晓宁，孙丽君.一种改进的小波阈值信号去噪方法［J］.电子科技，2012，25(11):15-17.

ZHANG Xiaoning，SUN Lijun.An Improved Wavelet Threshold Signal Denoising ［J］.Electronic Technology，2012，25(11):15-17.

［4］吴军.长途油气管道破坏预警的干涉型分布式光纤传感系统定位技术研究［D］.重庆:重庆大学光电工程学院，2007.

WU Jun.Study on Locating Technology of Distributed Optic-Fiber Sensing System Based on Interfering Principle for Long-distance PipelinesSabotageActs ［D］. Chongqing:DepartmentofOpto-Electronic Engineering， Chongqing University，2007.

［5］郝文广，丁常富，梁娜.小波降噪与FFT噪比较［J］.电力科学与工程，2011，27(3):59-61.

HAO Wenguang，DING Changfu，LIANG Na.Wavelet Noise Reduction Compared with FFT Noise ［J］.Electric Power Science and Engineering，2011，27(3):59-61.

［6］王利众.切比雪夫带通滤波器的设计［J］.凯里学院学报，2010，28(3):23-24.

WANG Lizhong.Design of Chebyshev Bandpass Filter［J］.Carey College，2010，28(3):23-24.

［7］刘艳霞，董蓓蓓，刘钰，等.基于小波阈值的医学图像去噪研究［J］.电视技术，2012，36(19):183-185.

LIU Yanxia，DONG Beibei，LIU Yu，et al.Reasearch of Medical Image Denoising Based on Wavelet Threshold ［J］.TV Technology，2012，26(19):183-185.

［8］赵瑞珍，宋国乡，王红.小波系数阈值估计的改进模型［J］.西北工业大学学报，2001，19(4):625-628.

ZHAO Ruizhen，SONG Guoxiang，WANG Hong.Improved Model of Wavelet Coefficients Estimated Threshold ［J］.Northwestern Polytechnical University，2001，19(4):625-628.

［9］行鸿彦，唐娟.时延估计方法的分析［J］.声学技术，2008，27(1):111-113.

XING Hongyan，TANG Juan.Analysis of Delay Estimation Method［J］.Acoustic Technology，2008，27(1):111-113.