过失速机动变指数趋近律UAS-SMC设计

艾文磊，王玉惠，朱林泽，许昌亮

(1.南京航空航天大学自动化学院，南京210016;2.福建省军区司令部电视侦收站，福州350003)

0 引言

放宽静稳定性(RSS:Relaxed Static Stability)的战斗机在过失速机动过程中可能会进入一种危险的状态——深失速，深失速的改出通常需要设计控制律［1，2］。飞机在深失速区域具有强耦合、时变、模型不确定等特点，而且也容易受到外界环境等因素的干扰，这类非线性系统控制要求具有较高的鲁棒性。

解决非线性控制问题的方法有很多，其中滑模控制较为突出［3-9］。但系统状态到达滑模面时会在滑模面的两侧来回变化，从而形成抖振，很难工程应用。针对滑模变结构控制中的抖振问题，有学者提出了一种新的单向辅助面滑模控制(UAS-SMC:Unidirectional Auxiliary Surfaces-Sliding Mode Control)［10，11］方法。该滑模控制能有效抑制抖振，提高控制品质，但收敛速度比传统滑模慢。为提高收敛速度，文献［12］提出了指数趋近律的单向辅助面滑模控制，但指数趋近律的切换带为带状，容易在原点处形成高频抖振。文献［13］提出了一种变指数趋近律，但只是针对传统滑模的抖振问题。

针对上述问题，笔者采用基于变指数趋近律的单向辅助面滑模控制解决战斗机过失速机动中非线性问题。首先对系统进行T-S建模［14］;然后根据单向辅助面滑模控制器设计方法及系统模型，设计了基于变指数趋近律的单向辅助面滑模控制器;论证了基于变指数趋近律的单向辅助面滑模的可达性及系统的稳定性;最后，给出了不同控制律下的仿真图及对比分析，验证了所提方法的有效性。

1 问题描述

战斗机过失速机动中的深失速改出的控制律设计问题通常考虑如下短周期运动方程

令x1=α，x2=q，u=δ，由文献［15］中的气动数据可写为f(x)，可写为g(x)，式(1)可表示为

其中x=［x1，x2］为系统状态;u为系统输入且满足限幅条件u∈［－25，25］;f(x)，g(x)只在u的某些分界点已知的，即u=－25(负满偏)，则f(x)=f1(x)，g(x)=g1(x)，u=25(正满偏)，f(x)=f5(x)，g(x)=g5(x)，同理fk(x)，gk(x)(k=2，3，4)也可获得。由于通常文献会给出舵面偏转某个角度时的气动参数具体表达式，从而确定此时的飞机数学模型。而两个相邻fk(x)，gk(x)(k=1，…，5)之间数学模型则是未知的，但可通过插值得到。因此，依据飞机飞行特性，将 u的分界点确定为u={－25，－10，0，10，25}。通常对此类问题的处理会使f(x)，g(x)在分界点处发生突变，控制器的设计变得困难。基于T-S模糊控制的思想，以上述非线性系统控制量在某分界点处的非线性方程作为规则，并通过模糊隶属度函数，使系统变得更平滑，易于设计控制器。

基于以上分析，非线性模型(2)的局部模型规则k为

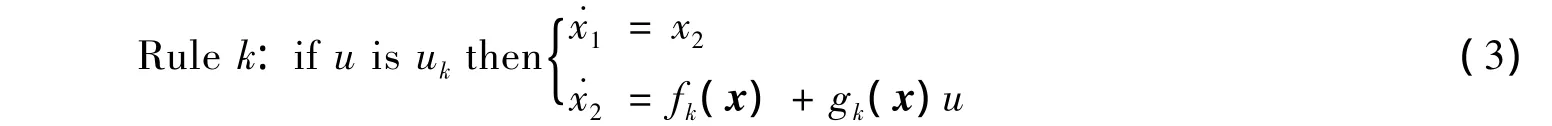
对于整个区间，系统可描述为

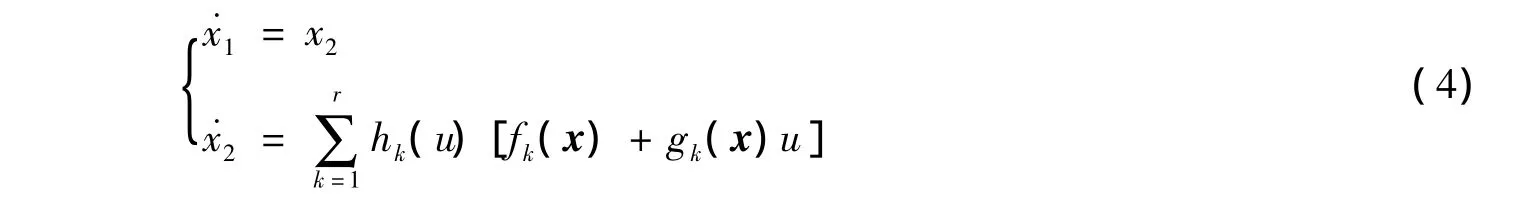
由于控制u的设计时基于模糊规则(3)，而u又是该规则的前件变量，因此在实际操作时，应先给出u的初始值，以保证系统正常运行。

2 单向辅助面滑模控制器设计

针对系统(4)，避免传统滑模的抖振缺陷，采用基于单向辅助面滑模方法设计控制器u［10］。首先给出单向辅助面的设计，具体过程如下所述。

2.1 单向辅助面设计

图1中，S1i，S2i为切换面。表达式为

2)设计单向辅助面。单向辅助面如图2所示。

图1 切换面示意图Fig.1 Switching surface

图2 单向辅助面示意图Fig.2 Unidirectional auxiliary surfaces

点 PS1i+，PS1i－，PS2i+，PS2i－组成凸四边形，线段 PS1i+PS2i－，PS1i－PS2i－，PS1i+PS2i+，PS1i－PS2i+构成单向辅助面 H0i，H1i，H2i，H3i，单向辅助面方程如下

其中 j∈{0，1，2，3};ωji1≠0;Mi＞0 是常数。

当前第i个单向辅助面

其中 ωi1，ωi2为

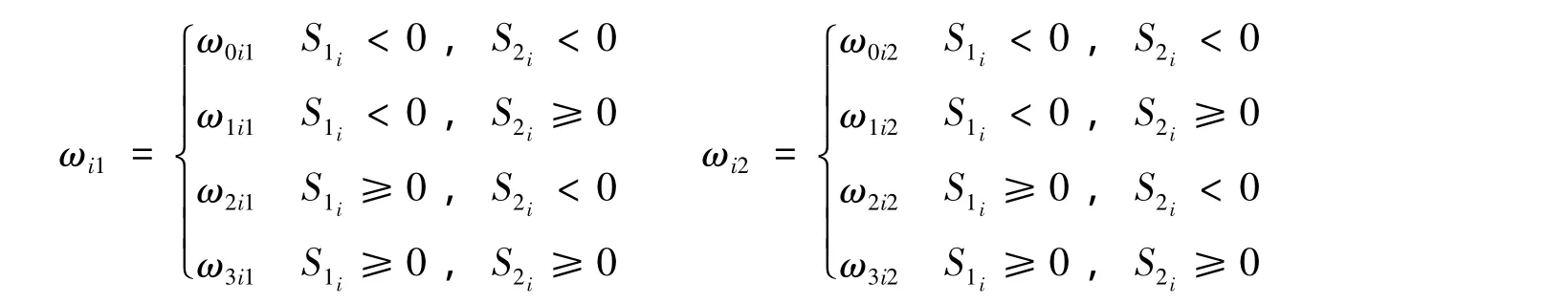
当前辅助面可记为

其中 H=［H1，…，Hn］T;ω1=diag{ω11，…，ωn1};ω2=diag{ω12，…，ωn2};M=［M1，…，Mn］T。

对于系统(4)，由于x1=∫x2，故切换面可设计为

单向辅助面为

2.2 基于变指数趋近律单向辅助面滑模控制器设计

滑模运动通常分为趋近运动和滑模运动两个过程，系统状态从任意初始位置趋向切换面，直到切换面的运动为趋近运动。滑模可达性条件仅能保证系统状态在空间任意位置到达滑模面，趋近运动的轨迹不受限制，采用趋近律的方法能改善趋近运动的动态品质。

2.2.1 趋近律的设计

单向辅助面滑模的指数趋近律［12］

其中ε，λ是可调参数，用来调整系统的收敛速度。ε＞0，λ＞0，N是趋近律。采用指数趋近律可以缩短系统的趋近时间，克服单向辅助滑模控制收敛速度慢的缺点。但系统在指数趋近律的切换带中向原点运动时，不能收敛于原点，而是在原点附近抖动，这就增加了控制器的负担。为此对指数趋近律进行如下改进

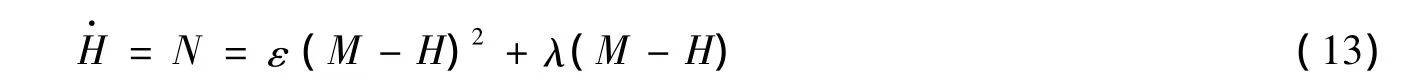
对比式(12)和式(13)发现，式(13)引入了(M－H)2。在初始阶段，由于系统状态离原点较远，(M－H)2较大，趋近速度较快;随着控制器的调节，系统将逐渐趋近原点，(M－H)2变小，使系统能平滑到达原点且在原点处的抖振也将变小。

趋近律(13)既能克服指数趋近律中滑模运动为带状的缺点，保证趋近过程的快速性，又能有效减少进入滑模面的初始系统抖动。该趋近律使状态变量不断趋向原点，抖振幅值不断减小，系统进入稳态后，稳定于原点，抖振现象消失，有效解决了常规指数趋近律单向辅助面滑模的抖振问题。

2.2.2 基于变指数趋近律的单向辅助面滑模控制器设计

对式(11)两边求导可得

式(14)和式(13)联立，可得

将系统(4)代入式(15)中，可得基于变指数趋近律的单向辅助面滑模控制器

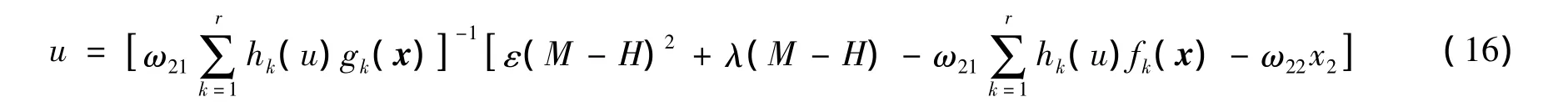
2.3 基于变指数趋近律的单向辅助面滑模的可达性和稳定性分析

2.3.1 基于变指数趋近律的单向辅助面滑模的可达性

对式(17)两边求导，由于Mi是常数，可得

式(15)代入式(18)可得

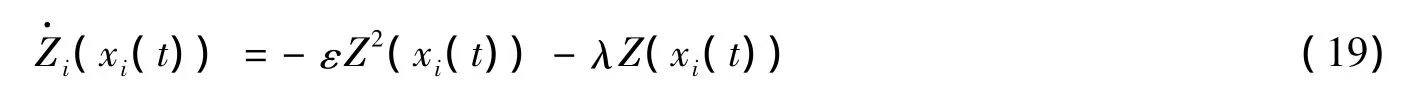
求解微分方程(19)可得

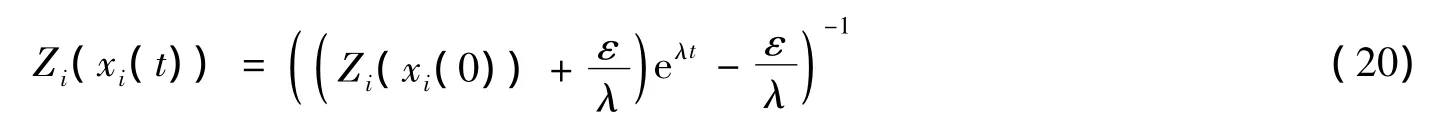
由式(20)可知，当t→∞时，Zi(xi(t))→0。

假设t=T(T足够大)时，Zi(xi(t))=0，t1为系统到达滑模面的时间。由文献［10］可知，当Zi(xi(t))=0时，系统到达原点。如果系统状态运动轨迹到达原点时首次到达滑模面，则t1=T;如果系统状态运动轨迹到达原点前已经到达滑模面并在滑模面上滑行至原点，则t1＜T。因此，系统状态可在时间T内到达滑模面，满足可达性。

2.3.2 基于变指数趋近律的单向辅助面滑模满足稳定性

由2.3.1节知，系统状态xi(t)能到达滑模面(S12和S22)，故只需要证明系统在滑模面上是稳定的。不妨选取切换面对切换面求导可得

选Lapunov函数为 V=xTx为正定二次型，V＞0，当且仅当 x=［0，0］T时，V=0。当 x≠0时，，由式(21)得

其中ξ1＞0。当x≠0时，˙V＜0。

同理可证，系统在切换面S22上也是稳定的。因此，系统状态x=［x1，x2］T是渐进稳定的。

3 仿真验证

采用非线性系统(4)验证所设计控制方法的有效性。

3.1 设计切换面

选择切换面为

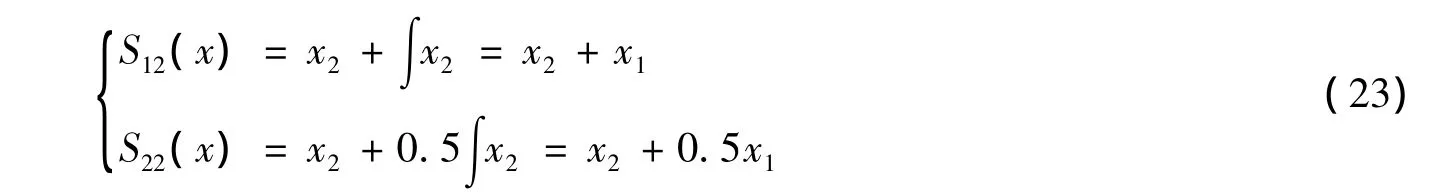
3.2 设计单向辅助面

在切换面上选取4 个点，分别为 PS11+=(－0.55，0.55);PS11－=(0.55，－0.55);PS21+=(－0.25，0.5);PS21－=(0.25 ，－0.5)。取 M=1，由以上4点可得到辅助面方程

则

3.3 设计控制器

假设初始状态为x1(0)=0，x2(0)=－0.5。基于变指数趋近律的单向辅助面滑模控制器取 ε =0.5，λ =0.5。

3.4 仿真验证

为验证所设计控制律的鲁棒性，在系统中加入干扰η=0.1sin(t)。笔者给出了相同条件下，基于指数趋近律的单向辅助面滑模控制器、基于变指数的单向辅助面滑模控制器作用下的对比仿真图如图3～图6所示。

图3 基于指数趋近律的单向辅助面滑模控制器u仿真图Fig.3 Sliding mode controller with unidirectional auxiliary surfaces based on exponent trending law

图4 基于指数趋近律的单向辅助面滑模状态仿真图Fig.4 Sliding mode state with unidirectional auxiliary surfaces surfaces based on exponent trending law

图5 基于变指数趋近律的单向辅助面滑模控制器u仿真图Fig.5 Sliding mode controller with unidirectional auxiliary surfaces based on improved exponent trending law

图6 基于变指数趋近律的单向辅助面滑模切换面仿真图Fig.6 Sliding mode state with unidirectional auxiliary surfaces based on improved exponent trending law

对比图3、图5，指数趋近律单向滑模辅助面滑模控制器具有明显的抖振现象;加入变指数趋近律后，控制器的抖振现象得到了明显的抑制。比较图4、图6可知，指数趋近律的单向辅助面滑模状态在收敛过程中都有较严重的抖振，基于变指数趋近律的单向辅助面滑模状态在收敛到原点时有轻微的抖振，系统进入稳态后，稳定于原点时，抖振现象消失。

为进一步验证变指数趋近律单向辅助面抑制抖振的效果，改变初始状态为x1(0)=0，x2(0)=－0.8，分别加入基于变指数和指数趋近律的单向辅助面滑模控制器得到系统状态x2的仿真图如图7所示，x12为基于指数趋近律单向辅助面滑模控制的系统状态x2，x22为基于变指数趋近律单向辅助面滑模控制的系统状态x2。由图7发现，变指数趋近律的单向辅助面滑模在系统状态远离原点时收敛速度比指数趋近律的单向辅助面滑模要快，当系统状态接近原点时，收敛速度变慢实现与滑模面平滑对接，基于变指数趋近律的单向辅助面滑模控制即保证了系统的收敛速度，也削弱了抖振。

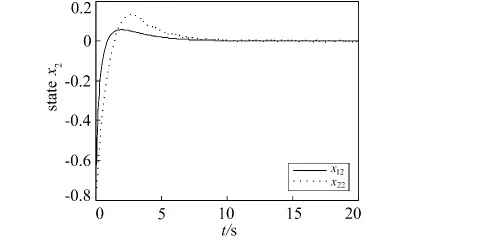
图7 基于变指数和指数趋近律的单向辅助面滑模状态x2的仿真图Fig.7 Sliding mode state x2with unidirectional auxiliary surfaces based on improved exponent trending law and exponent trending law

4 结 语

笔者从抑制指数趋近律单向辅助面滑模控制的抖振出发，提出了一种基于变指数趋近律的单向辅助面滑模控制方法，并结合战斗机非线性模型，给出了控制策略的设计方法和步骤。通过仿真分析，基于变指数滑模控制方法可以有效抑制抖振现象，系统进入稳态后，抖振现象消失，有效抑制了常规指数趋近律单向辅助面滑模控制的抖振问题。

［1］周欲晓，刘昶，尹江辉.RSS飞机深失速仿真研究［J］.飞行力学，1996，14(4):19-24.

ZHOU Yuxiao，LIU Chang，YIN Jianghui.The Simulation Study of Deep-Stall Characteristics for RSS Airplane ［J］.Flight Dynamics，1996，14(4):19-24.

［2］余勇军，尹江辉，刘昶.RSS飞机深失速走廊特性分析［J］.飞行力学，1998，16(2):1-6.

YU Yongjun，YIN Jianghui，LIU Chang.Analysis of Deep-Stall Corridor Characteristics for RSS Aircraft［J］.Flight Dynamics，1998，16(2):1-6.

［3］胡剑波，李飞，魏高乐，等.不确定系统反推滑模变结构理论及其应用［J］.系统工程与电子技术，2014，36(3):519-524.

HU Jianbo，LI Fei，WEI Gaole，et al.Theory and Applications of Backstepping Sliding Mode Variable Structure Control for Uncertain Systems［J］.System Engineering and Electronic Technology，2014，36(3):519-524.

［4］张晓宇，苏宏业.滑模变结构控制理论进展综述［J］.化工自动化及仪表，2006，33(2):1-8.

ZHANG Xiaoyu，SU Hongye.Overview of Sliding Mode Variable Structure Control［J］.Control and Instruments in Chemical Industry，2006，33(2):1-8.

［5］LAI Yinan，DAI Ye，BAI Xue，et al.Discrete Variable Structural Optimization Based on Multi-Directional Fuzzy Genetic Algorithm［J］.Chinese Journal of Mechanical Engineering，2012，25(2):255-261.

［6］KANG B P，JU J L JU.Sliding Mode Controller with Filtered Signal for Robot Manipulators Using Virtual Plant/Controller［J］.Mechatronics，1997，7(3):277-28.

［7］LEVANT A.Sliding Order and Sliding Accuracy in Sliding Mode Control［J］.International Journal of Control，1993，58(6):1247-1263.

［8］FEI Li，HUA Longxie.Sliding Mode Variable Structure Control for Visual Servoing System ［J］.International Journal of Automation and Computing，2010，7(3):317-323.

［9］高宏宇，邵克勇，李艳辉.不确定系统的上界自适应动态神经滑模控制［J］.吉林大学学报:信息科学版，2010，28(5):292-297.

GAO Hongyu，SHAO Keyong，LI Yanhui.Upper Bound Adapitive Dynamic Neural Sliding Mode Control of Uncertain in Systems［J］.Journal of Jilin University:Information Science Edition，2010，28(5):292-297.

［10］傅健，吴庆宪，姜长生，等.带状态约束的非线性系统单向辅助面滑模控制［J］.控制与决策，2011，26(9):1288-1294.

FU Jian，WU Qingxian，JIANG Changsheng，et al.Robust Sliding Mode Control with Unidirectional Auxiliary Surfaces for Nonlinear System with State Constraints［J］.Control and Decision，2011，26(9):1288-1294.

［11］傅健，吴庆宪，姜长生，等.连续非线性系统的滑模鲁棒正不变集控制［J］.自动化学报，2011，37(11):1395-1401.

FU Jian，WU Qingxian，JIANG Changsheng，et al.Robust Sliding Mode Positively Invariant Set for Nonlinear Continuous System［J］.Acta Automatica Sinica，2011，37(11):1395-1401.

［12］胡田文，吴庆宪，姜长生，等.指数趋近律单向辅助面滑模控制［J］.电光与控制，2013，20(7):36-41.

HU Tianwen， WU Qingxian，JIANG Changsheng， et al.Exponential Approach Law for Sliding Mode Control with Unidirectional Auxiliary Surfaces［J］.Electronics Optics＆ Control，2013，20(7):36-41.

［13］席雷平，陈自力，张世华.改进指数趋近律的机械臂滑模控制律设计 ［J］.计算机测量与控制，2012，20(2):380-382.

XI Leiping，CHEN Ziji，ZHANG Shihua.Design of a Sliding Mode Control Scheme Based on Improved Exponent Trending Law for Robotic Manipulators［J］.Computer Measurement＆ Control，2012，20(2):380-382.

［14］李艳辉，冯岩.基于 T-S模型的连续搅拌反应釜鲁棒 L2L∞控制［J］.吉林大学学报:信息科学版，2014，32(3):247-253.

LI Yanhui，FENG Yan.Robust L2L∞Control for Continuous Stirred Tank Reactor Based on T-S Model［J］.Journal of Jilin University:Information Science Edition，2014，32(3):247-253.

［15］NGUYEN L T，OGBURN M E，GILBERT W P，et al.Simulator Study of Stall/Post-Stall Characteristics of a Fighter Airplane with Relaxed Longitudinal Static Stability［R］.Virginia:Langley Research Center，1979.