CDKF 算法在四旋翼飞行器组合导航系统中应用

袁赣南，赵自超，贾鹤鸣，刘利强，戴运桃

(1.哈尔滨工程大学a.自动化学院;b.理学院，哈尔滨150001;2.东北林业大学机电工程学院，哈尔滨150040)

0 引言

自20世纪80年代微机电系统(MEMS:Micro Electro Mechanical System)及其相关技术迅速发展，基于MEMS技术的微惯性测量单元(MIMU:Micro Inertial Measurement Unit)越来越多地应用于导航系统的设计中。在四旋翼无人飞行器的设计中，由于质量空间等要求，MIMU器件被广泛使用。但是，四旋翼无人飞行器使用的MEMS传感器精度较低，尤其受MEMS陀螺仪逐次启动参数误差和零偏不稳定等因素的影响，系统姿态参数发散较快，难以满足基于欧拉角的线性化误差模型对小失准角的假设，这将导致滤波器在较短时间内发散。由于全球定位系统(GPS:Global Positioning System)和MIMU具有极好的互补性，所以，通常采用GPS与MIMU组成的组合导航系统解决上述问题。同时还可降低成本，提供全球精确导航能力。传统的组合导航系统能利用卡尔曼滤波算法对系统状态进行估计［1］，卡尔曼滤波算法是一种线性滤波方法，需要将系统模型线性化，只保留低阶项进行处理。然而，由于忽略了高阶项带来的影响，当失准角较大时，会带来较大的系统状态估计误差甚至导致滤波发散的现象。

在传统组合导航系统中，扩展卡尔曼滤波(EKF:Extended Calman filter)算法是应用最广也是最简单的一种高斯非线性滤波算法［2］。但由于EKF算法使用一阶泰勒展开，从而忽略了非线性函数高阶项的影响，一旦非线性度较强时，忽略的高阶项截断误差将对滤波精度产生较大影响，甚至导致滤波发散。同时，经线性化处理的系统噪声也不再满足高斯独立分布，在一定程度上增加了估计误差;而且在实际应用中，并不是所有的非线性函数均存在Jacobin矩阵，在一定程度上限制了EKF算法的应用。而中心差分卡尔曼滤波算法正好克服了EKF方法的缺点［3，4］，在滤波时不需要得到系统模型的具体解析形式，并充分考虑随机变量的噪声统计特性，与EKF算法相比较具有更小的线性化误差和更高的定位精度。中心差分卡尔曼滤波算法利用先验分布构造Sigma点，并使用线性回归变换后的Sigma点表示状态的后验分布，充分考虑了高斯随机变量的统计特性，与强行截断泰勒级数的EKF算法相比，避免了Jacobin矩阵的计算。

国内外学者对上述问题展开了大量的研究，文献［5］主要针对SINS_GPS紧组合在大失准角情况下出现的滤波发散现象，提出了一种基于中心差分卡尔曼滤波(CDKF:Central Difference Kalman Filter)的组合导航算法。文献［6］将自适应扩维UKF算法引入至SINS/GPS组合导航系统中，解决了含有白噪声的非线性系统的滤波问题。文献［7］设计并实现了基于多传感器数据融合的航向姿态参考系统，将卡尔曼滤波方法应用于实际的四旋翼无人飞行器硬件系统中。文献［8］使用四元数描述方法建立了GPS/SINS组合导航系统的非线性误差模型，并采用CDKF算法提高了整个系统精度。

上述研究为中心差分卡尔曼滤波算法提供了大量的理论支持，但该算法在实际中的应用较少，主要停留在仿真阶段。笔者针对四旋翼无人飞行器组合导航系统小失准姿态发散问题，将中心差分卡尔曼滤波算法应用于实际四旋翼无人飞行器平台中，将GPS与MIMU数据融合得到新的姿态反馈。通过实际数据分析可以看出，笔者设计的飞行器组合导航系统能有效抑制传感器噪声，克服了陀螺仪的漂移现象，克服了传统EKF算法的缺点，为飞行器提供准确的导航信息。

1 系统设计和系统模型

1.1 四旋翼无人飞行器组合导航系统

四旋翼无人飞行器的组合导航系统为飞行器控制系统提供一个准确的实时状态反馈，通过多传感器的信息融合技术，可弥补每个单独元件的缺陷，提高测量精度。针对任务需要，笔者选用MPU-6050芯片作为飞行器的姿态传感器，MPU-6050整合了3轴陀螺仪和3轴加速器，是全球首例整合性6轴运动处理组件，与其他多组件方案相比，省去了组合陀螺仪与加速器时间轴之差的问题，并减少了大量的空间。笔者设计的硬件系统如图1所示。

由于陀螺仪会随着时间的推移产生漂移现象，而且加速度计在飞行器飞行过程中容易受到震动等因素影响，单独使用姿态传感器难以获取准确的姿态反馈信息，从而影响飞行器的稳定控制。因此需要额外的位置观测量修正姿态传感器。

考虑到要获取准确的位置观测量，笔者选用了u-blox NEO-6M型号的GPS模块，瑞士u-blox是全球公认的民用最佳GPS模块厂家，许多高品质GPS产品也广泛采用此系列模块。飞行器MIMU系统硬件如图2所示，该模块质量轻、尺寸小，适合放置在四旋翼无人飞行器平台上。

图1 飞行器MIMU系统硬件Fig.1 Hardware of the quadrotor MIMU system

图2 GPS模块实物Fig.2 GPS module

1.2 系统模型

首先建立基于四元数的直接式导航系统非线性模型。选取北、东、地坐标系作为导航坐标系，其中S=［L λ h］T和V=［vNvEvD］T分别为飞行器的位置和速度。

定义载体的姿态四元数为QT=［q0qT］，q=［q1q2q3］T为向量部分，q0为标量部分。

笔者选择位置、速度、姿态四元数和陀螺漂移作为系统状态量，X=［S V Q εω］T，取位置、速度、磁场强度作为系统输出Z=［S V Bb］T，从而建立系统的非线性状态方程与量测方程。

可得到系统过程模型

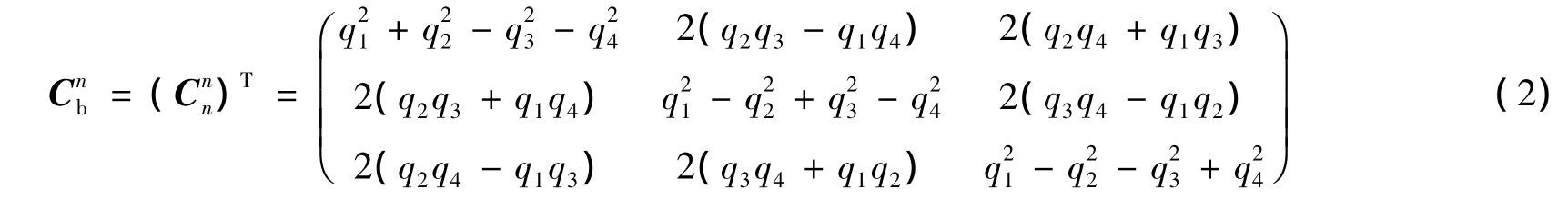
考虑到MIMU传感器精度较低和飞行器飞行速度较慢等因素，这里可以忽略地球自转和位置速率对飞行器角速率带来的影响。

可得到系统量测模型为

其中wp、wv分别表示GPS位置和速度的观测噪声，wb表示磁传感器观测噪声，笔者假设系统观测噪声为零均值高斯白噪声。Sk－N和Vk－N表示系统的位置和速度。

2 导航系统中的CDKF算法

2.1 算法原理与步骤

根据笔者所述的系统状态模型和量测模型，可将飞行器组合导航系统模型写为如下标准形式其中xk和zk分别表示k时刻系统状态和观测量，w和v分别为过程噪声和观测噪声，f(·)和h(·)分别表示非线性状态方程和观测方程。这里用x代替系统状态量X，用P表示协方差。选取系统的扩维状态为xa=［xTwTvT］T，包含了系统状态向量、系统过程和观测噪声向量。CDKF算法的具体计算步骤如下。

步骤1 系统变量初始化。系统的初始状态均值和协方差可表示为

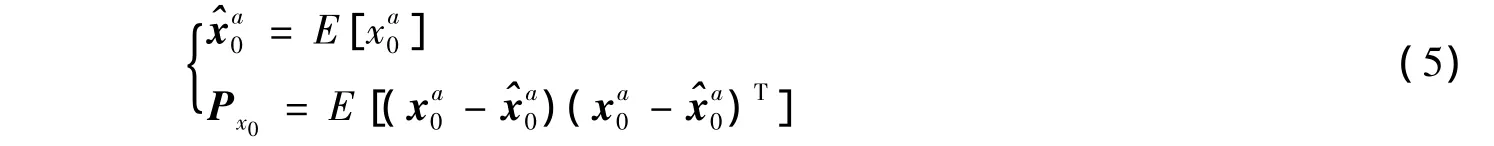
步骤2 时间更新。首先计算时间更新的Sigma点

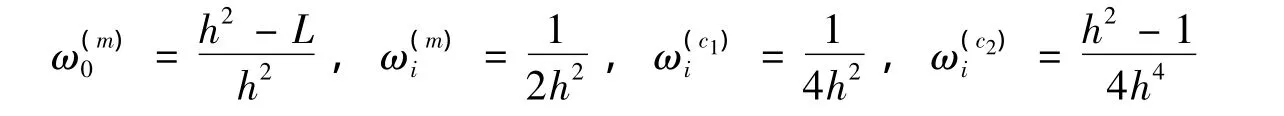
计算系统状态的时间更新，Sigma点沿非线性函数传播

步骤3 量测更新。笔者在MIMU/GPS组合模型中的观测方程使用了系统状态的位置、速度和GPS钟差等信息，由于不涉及到四元数运算，所以，仅在计算互协方差时需考虑四元数的影响。再计算Sigma点沿非线性函数h(·)的传播结果

得到随机向量沿非线性函数传播的后验均值、自协方差和互协方差分别为

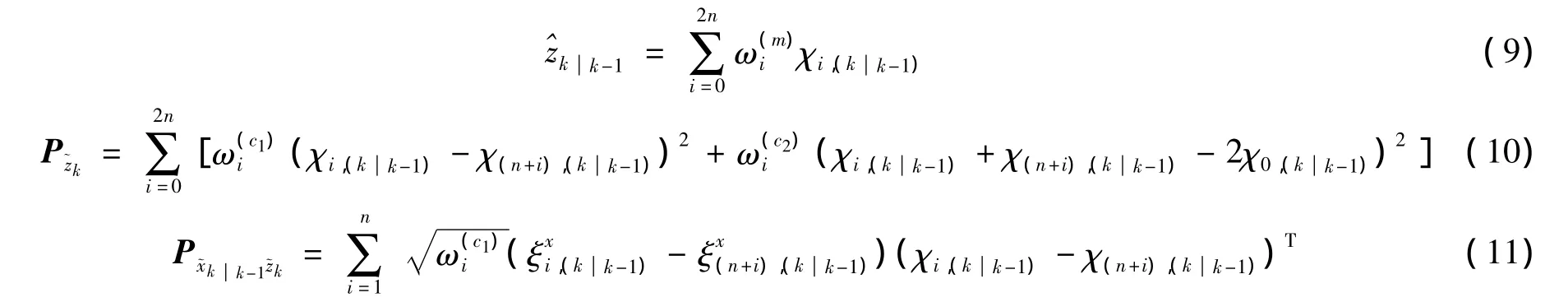
步骤4 根据量测数据，计算系统状态的后验分布

2.2 基于CDKF算法的飞行器组合导航系统

笔者在1.1节设计的四旋翼无人飞行器组合导航系统基础上，将CDKF算法移植到组合导航处理模块中。其软件流程图如图3所示。

由图3可知，组合导航系统应用中心差分卡尔曼滤波算法共分为6个步骤:

Step1 初始化;

Step2 计算Sigma点;

Step3 Sigma点权值计算;

Step4 系统状态时间更新;

Step5 系统状态量测更新;

Step6 系统状态后验分布。

其中传感器MPU-6050用于测量飞行器实时角速度与线加速度，GPS模块主要获取实时位置信息。在Step6将这些信息通过I2C总线传递到组合导航系统中，赋给式(14)中的观测变量zk。系统在执行完一次Step1后不再执行，之后循环执行Step2至Step6，完成MIMU与GPS之间的数据融合，克服MIMU中陀螺仪的漂移，最后得到系统状态估计值用于后续的飞行器控制。

3 实验分析

在设计的四旋翼无人飞行器组合导航系统上应用CDKF算法，在户外无风条件下进行实验，室外飞行实验效果如图4所示。

飞行器在空中共飞行了400 s，在机载处理器中将滤波前的MIMU解算数据与MIMU/GPS在应用CDKF算法后的解算数据分别保存，实时发送至上位机。在整个飞行控制中应用的是滤波后的导航信息。最后在Matlab软件中绘制成曲线图(见图5～图8)。

图3 组合导航系统软件流程图Fig.3 Software flow chart of the integrated navigation system

图4 四旋翼飞行器室外飞行实验Fig.4 Outdoor flight experiment of the quadrotor

图5 滤波前飞行器姿态Fig.5 The attitude of the quadrotor estimated without the CDKF algorithm

图6 滤波后飞行器姿态Fig.6 The attitude of the quadrotor estimated by the CDKF algorithm

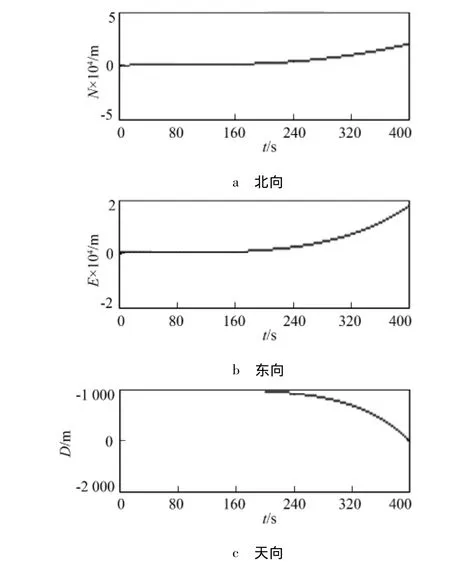
图7 滤波前飞行器位置Fig.7 The position of the quadrotor estimated without the CDKF algorithm

图8 滤波后飞行器位置Fig.8 The position of the quadrotor estimated by the CDKF algorithm

从图5和图7中可以看出，滤波前的飞行器姿态随着时间逐渐发散且趋势越来越快。飞行器的位置也呈指数发散，400 s后，飞行器的位置已经发散至几十千米，这样的结果在实际中是无法接受的。从图6中可以看出，机载组合导航系统在经过中心差分卡尔曼滤波算法处理后，其姿态数据变化不到1°，在400 s后偏差不超过2°，同时保持47°的偏航角且偏差不超过1°。从图8中可以看出，滤波后的飞行器位置没有发散现象且测量准确，整个飞行过程中，飞行器几乎悬停在一个点附近，偏差不超过2 m。

以上数据表明，笔者设计的基于中心差分卡尔曼滤波算法的四旋翼无人飞行器组合导航系统能有效抑制MIMU的漂移现象，避免了传统惯导的发散问题，且系统测量精度高，为飞行器的后续控制部分提供准确的导航数据。

4 结 语

笔者针对四旋翼无人飞行器组合导航系统中的小失准角发散问题，应用中心差分卡尔曼滤波算法，设计了一套GPS/MIMU组合导航系统。选用MPU-6050芯片作为飞行器的姿态传感器，GPS模块获取飞行器的实时位置。实际数据分析表明，该系统能有效抑制传感器噪声，克服了陀螺仪的漂移现象，克服了传统EKF算法的缺点，为飞行器提供准确的导航信息。

［1］赵琳，王小旭，丁继成，等.组合导航系统非线性滤波算法综述［J］.中国惯性技术学报，2009，17(1):46-52.

ZHAO Lin，WANG Xiaoxu，DING Jicheng，et al.Overview of Nonlinear Filter Methods Applied in Integrated Navigation System［J］.Journal of Chinese Inertial Technology，2009，17(1):46-52.

［2］PSIAKI M L.Attitude Determination Filtering via Extended Quaternion Estimation ［J］.Journal of Guidance，Control，and Dynamics，2000，23(2):206-214.

［3］ITO KAZUFUMI，XIONG Kaiqi.Gaussian Filter for Nonlinear Filtering Problem ［J］.IEEE Transactions on Automatic Control，2000，45(5):910-927.

［4］王璐.四旋翼无人飞行器控制技术研究［D］.哈尔滨:哈尔滨工程大学自动化学院，2012.

WANG Lu.Research on Control Technology of Quadrotor Unmanned Aerial Vehicle［D］.Harbin:College of Automation，Harbin Engineering University，2012.

［5］贾鹤鸣，宋文龙，牟宏伟，等.ISR-CDKF在SINS大方位失准角初始对准中的应用［J］.吉林大学学报:信息科学版，2013，31(2):196-202.

JIA Heming，SONG Wenlong，MU Hongwei，et al.Application of ISR-CDKF in Initial Alignment of Large Azimuth Misalignment in the SINS［J］.Journal of Jilin University:Information Science Edition，2013，31(2):196-202.

［6］孙尧，马涛，高延滨，等.自适应扩维UKF算法在SINS/GPS组合导航系统中的应用［J］.智能系统学报，2012，7(4):345-351.

SUN Yao，MA Tao，GAO Yanbin，et al.An Adaptive Augmented Unscented Kalman Filter with Applications in a SINS/GPS Integrated Navigation System［J］.CAAI Transactions on Intelligent System，2012，7(4):345-351.

［7］姜强，曾勇，刘强，等.四旋翼飞行器姿态航向参考系统设计与实现［J］.控制工程，2013，20(S):167-169，172.

JIANG Qiang，ZENG Yong，LIU Qiang，et al.Design and Implementation of Attitude and Head Reference System for Quadrotor Aero-Vehicle［J］.Control Engineering of China，2013，20(S):167-169，172.

［8］王海勃，陈红林，韩惠珍.CDKF在 GPS_SINS组合导航系统非线性模型中的应用［J］.现代电子技术，2011，34(11):19-22.

WANG Haibo，CHEN Honglin，HAN Huizhen.Application of CDKF Method in GPS/SINS Integrated Navigation System Nonlinear Model［J］.Modern Electronics Technique，2011，34(11):19-22.