基于遗传算法的三维模型匹配方法

叶建华， 高诚辉， 江吉彬

(1. 福州大学机械工程及自动化学院，福建 福州 350108；2. 福建工程学院机械与汽车工程学院，福建 福州 350108)

基于遗传算法的三维模型匹配方法

叶建华1,2， 高诚辉1， 江吉彬2

(1. 福州大学机械工程及自动化学院，福建 福州 350108；2. 福建工程学院机械与汽车工程学院，福建 福州 350108)

逆向测量模型与正向设计模型的自动匹配是三维检测的关键技术之一。通过空间六自由度的旋转与平移变换调整模型方位，基于K-D树和拓扑信息获取三维模型与不同方位平面的相交轮廓。利用二维相交轮廓的差异度作为两模型间的匹配判据，避免海量数据点与复杂曲面间的直接匹配计算。采用遗传算法进行两模型最佳匹配方位的求解，以空间六自由度为个体的染色体，通过群体的多点搜索，历经选择、交叉、变异操作，得到全局最佳匹配方位。通过实例验证了方法的有效性。

模型匹配；三维模型；遗传算法；归一化

随着自由曲面在汽车、船舶、航空、航天和模具等领域的广泛应用，对其制造精度的检测也变得越发重要。由于传统的自由曲面检测方法需要有足够的测量空间、确定的测量基准和专用的模板检具，难以实现高精、高效测量。而随着三维数字化扫描精度、测量效率的不断提高，三维检测技术得到快速发展与应用。三维检测技术采用三维数字化扫描设备获取零部件的三维网格测量模型，并与正向设计的数字化模型进行匹配，进而通过误差分析评估制造精度。其中三维网格测量模型与正向设计CAD模型的匹配是三维检测技术的关键。

模型匹配的目的在于建立一致的误差分析基准。由于从三维数字化扫描设备所获得海量点云数据构成的三角网格数据模型与正向设计的三维CAD模型之间的坐标系统没有任何关联，因此，在分析之前需要匹配两模型的方位，实现测量坐标系与设计坐标系的统一。目前，基于形状的自适应匹配方法[1]是模型匹配的研究重点，诸多学者开展了相关研究。常用的主元分析法(principal component analysis，PCA)[2]通过主轴进行匹配，提供了每根主轴的方向，但当模型采样不一致时，会导致主轴的不确定，主要作为初匹配方法。传统的迭代近邻点算法(iterative closest point，ICP)[3]是基于优化理论对海量数据点进行近邻匹配调整，是一种精确匹配方法，但该方法易受初始点云位置的影响，不能保证收敛。Claudet[4]提出的基于点云与 NURBS曲面的匹配方法、Pottmann和Leopoldseder[5]提出的基于点云速度场的配准方法是直接基于三维信息进行匹配，处理的数据量大，算法的收敛性及效率不易保证。由于二维图形图像处理技术的研究已较成熟，且算法简单，出现了基于视觉图像相似性实现标准化坐标系的方法[6]，通过模型的自动旋转和多视点图像的比较，将坐标系逐渐标准化，该方法是一种穷举搜索法。遗传算法(genetic algorithm, GA)是一种通过模拟自然进化过程搜索最优解的全局搜索算法，它采用群体的方式进行多点搜索，经交叉操作实现个体的遗传进化逐步产生最优个体，并利用变异操作避免陷入局部极值。鉴于上述算法的不足，结合二维图形算法的高效性和遗传算法的鲁棒性，本文提出通过三维模型不同方位的二维轮廓图进行匹配度评测，并采用遗传算法进行两数据模型最佳匹配方位的全局搜索，从而实现匹配算法的效率与鲁棒性。

1 匹配模型建立

模型匹配就是在三维空间中求解两模型的最佳一致姿势方位。设测量获得的三角网格模型为调整模型 A，正向设计的数字化模型为参考模型S，则模型匹配过程就是在参考模型S固定不动的情况下，通过旋转、平移操作将原本处在任意位置、姿态的调整模型A调整到与参考模型S相一致的位置。也就是要使以下目标函数最小：

其中ia为模型A的顶点；si为ai到参考模型S的最近点；R为调整姿态的旋转变换矩阵：

α、β、γ为模型A分别绕Z、Y、X轴旋转角度；T为调整位置的平移变换矩阵：

l、m、n为模型A沿X、Y、Z三个坐标方向的平移量。

可知，两模型的匹配，就是要找到一组α、β、γ、l、m、n值，使得ε最小。

2 匹配度评测方法

ε值的计算过程也就是两模型方位匹配度的评测过程。正向设计模型是包含自由曲面的复杂CAD模型，逆向测量模型是包含海量数据点的三角网格模型，若直接基于三维数据模型进行匹配度评测值ε的计算，则计算方法复杂、效率低下。为了简化ε值的计算复杂度、提高算法效率，本文把三维模型的匹配度ε评测，转化成二维相交轮廓图的相似度D的评测。算法的基本思路为：把正向的CAD模型S进行离散化得到三角网格数据模型S′，然后用不同方位的平面与三角网格数据模型 A、S′进行求交，得到相交的二维轮廓图，接着基于这些二维轮廓图定义定量的度量标准和匹配度评测方法。

2.1 三维CAD模型网格化

为了不同方位的平面与三角网格数据模型A、正向的CAD模型S的求交方法的统一，需要将正向设计的三维CAD模型S离散，并转化成三角网格模型S′。三维CAD模型是由NURBS曲面包裹而成，模型的网格化也就是对多张NURBS曲面的离散和离散点的三角化剖分。

NURBS曲面的参数化表达式[7]为：

式中， Qij( i =0,1,… ,n; j =0,1,… ,m)为网格控制顶点， Wij( i =0,1,… ,n; j =0,1,… ,m)为网络控制点的权值， Ni,k(u)为NURBS曲面u参数方向的B样条基函数，Nj,l(v)为NURBS曲面v参数方向的B样条基函数，k、l为B样条基函数的阶次。

由式(2)可知，对NURBS曲面的三角网格化可以转化为：先在参数域上对 u∈ [0,1]，v ∈ [0,1]的二维平面进行离散并网格化，然后从参数域映射回欧式空间实现NURBS曲面的网格化。在参数域上进行离散时，为了实现三角面片的粒度与扫描获得的一致，确定u、v方向的平均初始离散步长 Δu 、Δv为：

式中，Area为 NURBS曲面控制多边形网格的面积，a rea _ trii( i = 0,1,… ,N)为三角网格模型A中三角面片的面积。在离散过程中通过曲率半径值调整离散步长 Δu、 Δv：若 Δu＞ K ρu,Δu= K ρu；若Δv＞ K ρv,Δv= K ρv；ρu和 ρv分别为上一离散点沿u、v方向的曲率半径，K为比例系数。对离散获得的采样点，根据邻接关系进行三角化剖分，从而得到参数域上的网格剖分结果。然后通过式(2)映射回欧式空间得到每张 NURBS曲面的网格模型子集。对网格模型子集进行拼接即可得到三角网格化模型S′。

2.2 截交平面

由于用同一组包含不同方位的平面去截取不同位置、姿势的三维模型所得的相交轮廓会有差异，因此，提出利用相交轮廓的差异度来度量两模型的匹配度。采用参考模型坐标系统的三个正交面和模型包围盒缩小 1/3得到正六面体的表面延伸面作为获取三维模型轮廓图的切割平面，所得到的相交轮廓能同时反映模型的总体特征和局部细节特征。其中参考模型坐标系统的原点设置在模型包围盒的中心。在最佳一致位置的求解过程，模型 A的位置与姿势需要不断地调整。由于模型 A包含的数据量大，相应的调整过程计算量也大，而平面的方位调整却很简单，因此本文采用切割平面的逆向变换来实现求解过程模型 A的不变换。即把由α、β、γ、l、m、n确定的调整模型A相对原点的旋转、平移变换A· R· T转化成由-α 、-β、-γ、-l、-m、-n值确定的上述9个切割平面的逆变换Planes· T ′·R ′，即调整模型A的切割平面为： Plani′ = Planei· T ′·R ′,(i =1,… ,9)。

2.3 三维网格模型与平面求交

二维轮廓图是通过三角网格模型S′、A与二维平面求交获得的。三角网格模型S′作为参考模型只需在初始时与上述 9个平面进行求交计算，而调整模型A在匹配过程中需要与不同方位的9个切割平面进行频繁地求交计算，求交算法效率直接决定着整个匹配方法的效率。为了保证效率，本文提出采用 K-D树检索每个相交轮廓的第一条边，进而利用拓扑关系搜索出其余相交边的方法。以调整模型A与切割平面 Plani′为例进行求交算法的说明：

(1) 建立调整模型 A的 K-D树。树节点为 q的K-D树具有时间复杂度为O( log2q)[8]的搜索速度。K-D树的每个节点在三维空间上表现为空间六面体，包含着属于这一节点的三角面片序列，同层节点通过平面识别器进行分割，并记录着指向下一层的左子树指针和右子树指针。根据调整模型 A所包含的三角面片规模确定最大层数和每个六面体节点中包含的三角面片个数。K-D树的根节点就是包含网格模型 A的所有三角面片的包围盒，树的建构过程为：判别三角面片是在识别器平面哪一侧，根据判别结果归类到左、右子树三角面片序列中，如果三角面片与识别器平面相交则同时记录到左、右子树三角面片序列中；逐层递归分解，从而建构起一颗完整的K-D树。

(2) 利用K-D树检索每个轮廓的第一条边。逐层判断切割平面 Plani′与节点平面识别器的关系，如果不相交则判断在哪一侧；如果相交则求出交线，后续则用交线分割后的半平面去与平面识别器做判断；通过逐层判断获得切割平面 Plani′跨过的空间六面体所对应的叶节点。从叶节点中得到这一节点所包含的三角面片序列，并与切割平面Plani′求交，从而获得与 Plani′相交的第一条边。往往调整模型 A与切割平面 Plani′存在多个相交环，求得相交环后，还要重复去判断是否存在未求交过的三角形与切割平面 Plani′存在相交，从而获得下一个环的第一条边。

(3) 建立网格的拓扑信息。拓扑信息也就是拓扑元素的类型、个数以及相互之间关系的表达。通过拓扑信息可以快速地获得与拓扑元素相邻的几何元素。在网格模型的拓扑信息中建构以下拓扑关系：顶点相关的一阶领域边；边所包含的两顶点；边所对应的左、右三角面片；三角面片所包含的顶点与边。

(4) 利用拓扑信息搜索出其余相交边。以第一条边为搜索起点，利用拓扑关系获得边所对应的三角面片，进而获得三角面片所对应的其他边和顶点，并与切割平面iPlan′求交获得下一相交边；如果交点落在顶点上，则通过顶点获得其一阶领域边与切割平面iPlan′求交获得下一相交边。不断重复上述过程，直到又找到搜索起点边或向两个方向都找到边界边为止。求出与切割平面iPlan′相交的所有交点ikCa，即可得到一个完整的相交截面轮廓iCa。为了下个环第一条边的计算效率，求过交的边和所在的三角面片做已计算标记。

(5) 重复步骤(2)和(4)求出所有相交轮廓。

2.4 一致性判据

两模型位置与姿势的匹配程度通过截面轮廓图的相似度进行定量分析，而截面轮廓图相似度的评测一般由距离、边长、面积、角度等来度量。为了兼顾效率和鲁棒性，本文在截面轮廓点Huasdorff距离[9]的基础上，加入边长差来度量两个模型间的相似度：

其中， Csij、 Caik为参考模型S′、调整模型A与第i个截交面的交点， Csi、 Cai为参考模型S′、调整模型A与第i个切割面的相交多边形轮廓；DH为两个截交面轮廓点集中任意两点 Huasdorff距离的度量； LC为两个截面轮廓 Csi、 Cai的边长差的度量。R、T的变换变量值由α、β、γ、l、m、n确定。对 Caik和 Cai进行坐标变换的目的是把调整模型A与第i个切割面的截交点和截交轮廓变换到统一的坐标系统下进行相似度计算。

3 基于遗传算法的匹配

遗传算法[10]具有很强的鲁棒性，将其应用到两模型匹配上的基本流程为：对α、β、γ、l、m、n六个参量进行编码，进而产生初始群体；把两个模型间的相似度值D作为个体适应度的判断依据，历经选择算子、交叉算子、变异算子的遗传操作实现群体的进化，从而实现两模型的最优匹配。

3.1 编码

六个调整参量中，旋转调整量α、β、γ的最大取值区间为[- π,π]，平移调整量l、m、n的取值由两匹配模型的最小包围盒大小决定。六个参量α、β、γ、l、m、n在取值范围内任意值的组合为一个体。调整量的具体取值因模型而异，取值区间越小越容易收敛。基于调整参量的取值特点，采用归一化的浮点数编码方法进行编码，并随机产生M个初始个体。设某一个体的六个调整参量值为x1, x2,x3, x4,x5,x6，则个体的表现型描述为：X =[x1, x2,x3, x4,x5,x6]；对应的基因型为：T =[t1, t2, t3, t4, t5, t6]，其中bi、 ai是 xi的上下限。

3.2 适应度函数

两模型匹配的目的在于目标函数值D最小，且D值恒为正，因此目标函数 D( X)可以直接对应到搜索空间作为适应度函数： E( T ) = D( X)。而为了维护早期群体的多样性和避免早熟以及后期阶段个体间的无序竞争，对适应度尺度进行变换：E ′= exp(- δ E)，其中δ为尺度系数。

3.3 遗传算子设计

(1) 选择算子：根据群体中的个体适应度进行优胜劣汰。采用无回放式余数随机选择的方法[11]选择遗传到下一代的个体，以保证适应度值较大的一些个体能得到繁殖。首先，根据个体的适应度值占群体总适应度值的比例，计算该个体在下一代群体中的生存期望数目 ENi：

然后，用 ENi的整数部分确定该个体遗传到下一代的数目，从而确定出个个体遗传到下一代。剩余的个个体通过新的适应度值按选中概率与新适应度值的大小成正比的方法通过赌盘进行随机确定。

(2) 交叉算子：是GA产生新个体的主要方法，对遗传下来的个体以随机的方式两两组成交叉组，通过线性组合的方式进行交叉操作。设第g代的两个随机配对的个体则交叉操作后产生的新个体为：

其中σ为[0,1]上产生的随机数。产生的新个体要进行有效性判断，避免越界。交叉概率太大容易引起搜索过程的随机化，太小则容易引起早熟，本文取 Pc= 0.86。

(3) 变异算子：是产生新个体能力的辅助方法，目的在于改善局部搜索能力和避免早熟。采用均匀变异方法增加群体的多样性，依次指定个体染色体中的基因作为变异点，以变异概率 Pm确定该点是否进行基因变异，对要变异的基因进行随机变异。设个体 Tc在 tk处变异，随机变异的新基因值 tk′ = τ，τ为[0,1]上的随机数。取变异概率Pm= 0.068。

4 应用实例

利用Visual C++语言，在OpenGL技术的支持下开发了原型系统，验证了本文方法的可行性。图1是涡轮叶片的匹配实例。图1(a)为正向设计软件 Pro/ENGINEER creo 2.0建立的涡轮叶片三维CAD模型；图1(b)为离散化后的三角网格模型；图1(c)为离散化后的三角网格模型与9个切割面的相交轮廓图；图1(d)是从三维数字化扫描设备所获得的三角网格数据模型，包含198 436个三角形面片；图1(e)是目标函数的平均值和最小值经过120代进化的变化曲线，从图可看出GA的收敛趋势；图1(f)是匹配的结果；图1(g)是两模型的匹配偏差云图。根据匹配结果可知本文算法能进行有效的匹配。

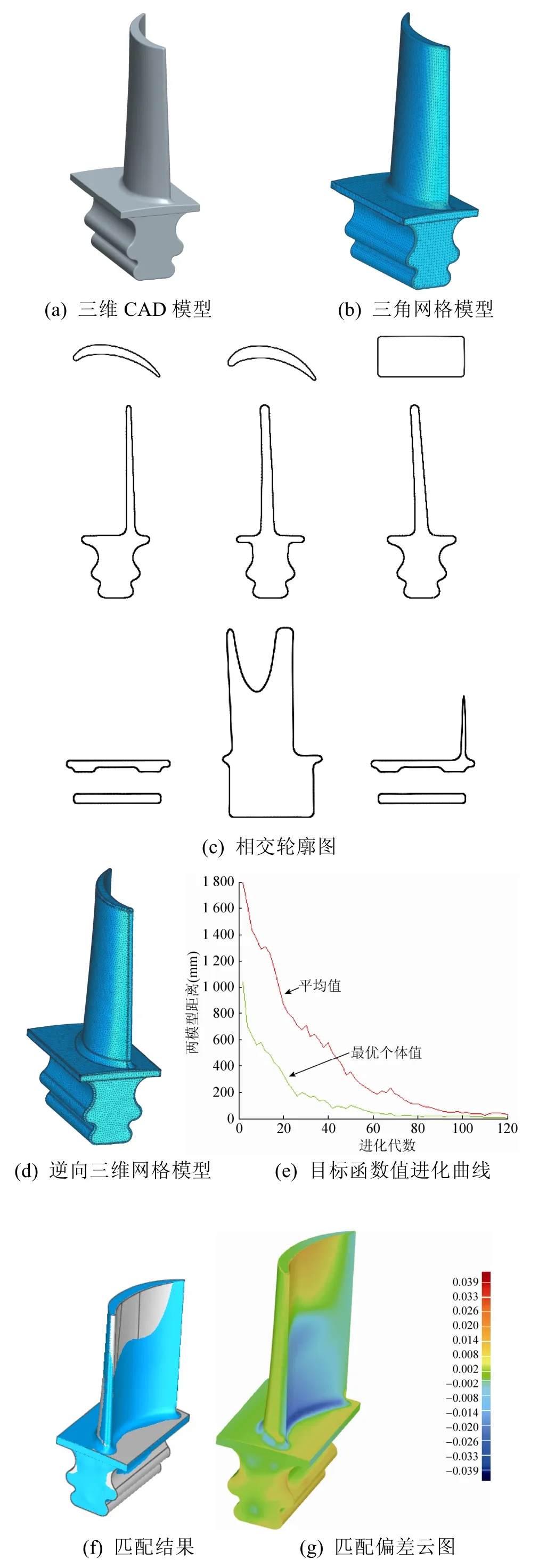
图1 涡轮叶片的匹配实例

图2是凸轮的匹配实例。图2(a)为正向设计软件SolidWorks 2013建立的凸轮三维CAD模型；图 2(b)是从三维数字化扫描设备所获得的三角网格数据模型，包含104 783个三角形面片；图2(c)是采用本文算法经过GA 120代进化后的两模型匹配偏差分析图；图 2(d)是在 Geomagic Studio2012中采用最佳拟合方式进行匹配后的误差分析图，可知两个模型有明显的错位。可知本文算法的匹配具有较好的鲁棒性。

图2 凸轮的匹配实例

5 结 论

本文构建了三维模型六个自由度匹配调整的数学模型。采用二维轮廓图间的Huasdorff距离与边长差的加权和作为模型匹配程度的判据，把实测数据的三角网格模型与三维CAD模型的匹配，转换成二维轮廓图形匹配度的度量，避免了海量数据点与复杂曲面的直接计算。在三维CAD模型三角化离散的基础上，基于K-D树和拓扑关系求三维模型与平面的交截轮廓图，避免了三维CAD模型与平面的直接求交，并有效提高了算法效率。以二维轮廓图间的差异最小为目标，用GA搜索两模型最佳匹配时的位置、姿势六参量，通过实例验证了该算法具有良好的鲁棒性和匹配精度。

[1]高 艺, 王 斌, 胡楷模, 等. 基于典型面匹配的机械零件检索方法[J]. 计算机辅助设计与图形学学报, 2011, 23(4)： 640-648.

[2]唐 勇, 沈 哲, 吕梦雅, 等. 改进的三维模型检索PCA预处理算法[J]. 系统仿真学报, 2008, 20(11)：2832-2835.

[3]Besl P J, Mckay N D. A method for registration of 3-D shapes [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence (S0162-8828), 1992, 14(2)： 239-255.

[4]Claudet A A. Analysis of three dimensional measurement data and CAD models [C]//PHD Dissertation of Georgia Institute of Technology, 2001： 45-56.

[5]Pottmann H, Leopoldseder S. A concept for parametric surface fitting which avoids the parameterization problem [J]. Computer Aided Geometric Design (S0167-8396), 2003, 20： 343-362.

[6]Tangelder J W H, Veltkamp R C. A survey of content based 3D shape retrieval methods [J]. Multimedia Tools and Applications, 2008, 39(3)： 441-471.

[7]施法中. 计算机辅助几何设计与非均匀有理B样条[M].北京： 高等教育出版社, 2001： 435-440.

[8]陈志杨, 叶建华, 沈 瑛, 等. 交叠网格的检测与合并[J]. 中国机械工程, 2008, 19(17)： 2064-2068.

[9]徐士彪, 车武军, 张晓鹏. 基于形状特征的三维模型检索技术综述[J]. 中国体视学与图像分析, 2010, 15(4)：439-450.

[10]董加强. 基于遗传算法的航天测控网资源分配模型与仿真[J]. 计算机应用, 2013, 33(7)： 2074-2077.

[11]杨 平, 郑金华. 遗传选择算子的比较与研究[J]. 计算机工程与应用, 2007, 43(15)： 59-62.

A 3D Models Matching Algorithm Based on Genetic Algorithm

Ye Jianhua1,2, Gao Chenghui1, Jiang Jibin2
(1. School of Mechanical Engineering and Automation, Fuzhou University, Fuzhou Fujian 350108, China; 2. School of Mechanical & Automotive Engineering, Fujian University of Technology, Fuzhou Fujian 350108, China)

Marching mesh model which get by measurement sensor to CAD model is one of key technology in geometrical parameter measurement. It is necessary to research the consistent match orientation and position for two models. In this paper, a 3D models matching algorithm was proposed based on genetic algorithm. The translation and rotation operations in three dimensional spaces to adjust the position and orientation are used, and 2D outline features was used to match the two models. Genetic algorithm is applied to searching the consistent match orientation and position for two models. The prototype system was developed and the results were reported. Based on practice, this method is robust and efficient.

model matching; 3D models; genetic algorithms; unitary coordinate

TP 391

A

2095-302X(2015)01-0022-06

2014-04-17；定稿日期：2014-08-05

国家自然科学基金资助项目(51305079)；福建省自然科学基金资助项目(2013J01168)；福建省教育厅A类科技资助项目(JA13216)；福建省省属高校科研资助项目(JK2012031)

叶建华(1980-)，男，福建宁德人，讲师，在读博士。主要研究方向为制造过程自动化及信息化。E-mail：yeuser@fjut.edu.cn

高诚辉(1953-)，男，福建福清人，教授，博士生导师。主要研究方向为摩擦学、表面工程、数字化设计。E-mail：gch@fzu.edu.cn