NURBS曲面自由型特征处理方法研究
李爱民, 牛秦玉, 寇发荣, 田海波
(西安科技大学机械学院,陕西 西安 710054)
NURBS曲面自由型特征处理方法研究
李爱民, 牛秦玉, 寇发荣, 田海波
(西安科技大学机械学院,陕西 西安 710054)
NURBS曲面自由型特征因不具有确定的参数、准确的边界,使其表示、编辑及操作十分困难。基于一种新的小波多分辨率分析技术将NURBS曲面从单一尺度几何表示的空域变换为频域的表示形式,借助于滤波器组将模型的整体结构和局部细节变换为其全局和局部多分辨率自由型特征,实现了对NURBS曲面的自由型特征的编辑、操作和控制。该方法不仅能提高NURBS曲面几何建模的效率,而且可以克服传统NURBS曲面建模的繁琐和费时。
NURBS曲面;自由型特征;B样条小波;多分辨率分析
NURBS曲面在计算机辅助设计、计算机图形学以及三维CAD/CAM技术中发挥着重要的核心作用,尤其在飞机、船舶、汽车等对曲面质量要求较高的产品设计中。在当前的大型商业化CAD/CAM系统中,比如CATIA、UG、Pro/E等,广泛采用了 NURBS张量积曲面来表示复杂的外形表面。
在几何建模过程中,特征技术不仅满足了高层次几何抽象的需要,而且有效提高了几何建模的效率。根据特征的不同构成特性,特征可划分为规则几何形状特征和自由型特征。规则几何形状特征因具有准确的几何定义,通过不同的参数设置可以简单地实现其特征的创建、编辑等功能,而对于自由型特征而言因其不具有确定的几何参数、而且其边界也是模糊的,则很难实现。由于受到NURBS曲面自由型特征固有特性的限制,在几何建模系统中尚不能够有效实现对自由型特征的处理。小波多分辨率几何建模技术将传统单一尺度几何空间的 NURBS曲面数学表示形式转换到多尺度空域和频域空间的多尺度频谱表示形式,从而实现了对 NURBS曲面自由型特征的处理。
均匀和准均匀 B样条曲面的多分辨率几何建模技术在国内外已进行了较为深入的研究,相关的理论和算法也比较成熟。但是,均匀和准均匀B样条曲面的多分辨率技术无法直接应用于NURBS曲面。当前,对非均匀 B样条曲面的多分辨率几何建模的研究还相对较少。主要是由Lyche等[1]、刘建等[2]、Li等[3]、Bertram[4]以及Pan和Yao[5]分别基于不同的非均匀B样条小波对非均匀B样条曲面进行了多分辨率几何建模研究。但这些小波形式都存在一些缺陷,如运算量较大或者仍然没有避免对 B样条节点向量的限制及其最小紧支撑特性无法得到一致性保证。在文献[6]中,作者提出了一种新的半正交非均匀 B样条小波,并建立了完整的理论和算法,此种小波不但应用方便,而且计算效率较高。本文基于此种小波多分辨率分析技术来研究NURBS曲面的几何建模,并有效实现了对其曲面整体与局部自由型特征的编辑、控制和处理。
1 二维半正交非均匀B样条小波
在 BS[a, b]空 间 嵌 套 的V0⊂ V1⊂…⊂ Vj⊂…子空间中,根据B样条节点插入理论, Vj和 Vj-1空间中基函数向量满足:Nj-1=NjPj,Pj为 (nj+ 1)× (nj-1+ 1)阶矩阵;Vj和Wj-1空间中基函数向量满足:ψj-1=NjQj,Qj为(nj+ 1)× mj-1阶矩阵。只要 Qj为列满秩矩阵,且:

那么 Wj-1空间必定是 Vj-1在 Vj空间中的半正交补空间,即 Vj=Vj-1⊕Wj-1,Vj-1空间和 Wj-1空间中的函数离散内积为零。ψj-1即为半正交非均匀 B样条小波, Wj-1就是 Vj-1的半正交小波补空间。
Vj-1和 Wj-1空间中基函数 Nj-1和ψj-1之间关系可以进一步表示为:
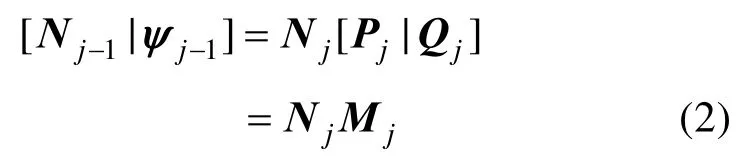
式(2)两端乘以 Mj-1可得到:

根 据 Vj=Vj-1⊕Wj-1, Vj中 任 意 函 数fj=Njdj则 可 以 分 解 为 两 部 分 :fj= fj-1+ gj-1=Nj-1dj-1+ψj-1wj-1, fj-1称为分解得到的 fj全局光顺部分, gj-1称为 fj的细节特征部分。
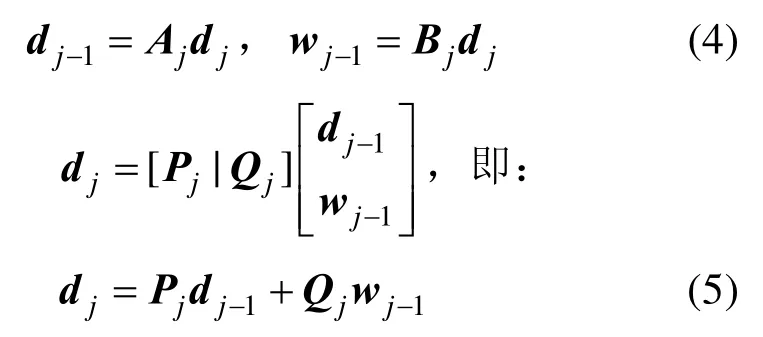
矩阵 Pj和 Qj称为小波重构矩阵,矩阵 Aj和 Bj称为小波分解矩阵。
在二维参数空间中,必须建立相应的二维小波基。二维小波基函数的标准构造包含了全部的一维基函数张量积。设在 L2[ a, b]空间中有嵌套空间[7-8]:…,及相应的细分尺度函数为 Nk1(u)和定义j尺度下的二维尺度空间为:
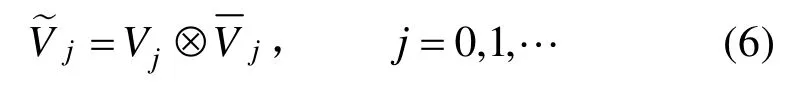
其中符号⊗表示空间相乘。
令 Wj和j分别为 Vj和j在 Vj+1和j+1空间中的半正交补空间,即:
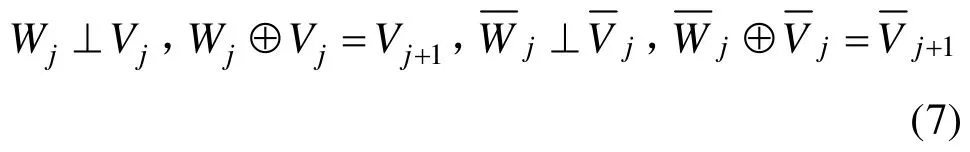
则:

2 NURBS曲面的多分辨率表示
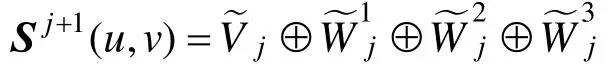
由NURBS曲面的齐次坐标表示可知,二维张量积NURBS曲面具有下面所述的矩阵表示形式:
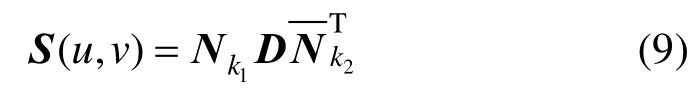
其中D为控制顶点矩阵,构成了NURBS曲面的控制多边形网格。 Nk1和分别为参数u和v的非均匀 B样条基函数向量。根据曲面的矩阵表示和二维张量积标准小波变换形式,˜1jV+空间上NURBS曲面的多分辨率数学表示具有下面的形式:
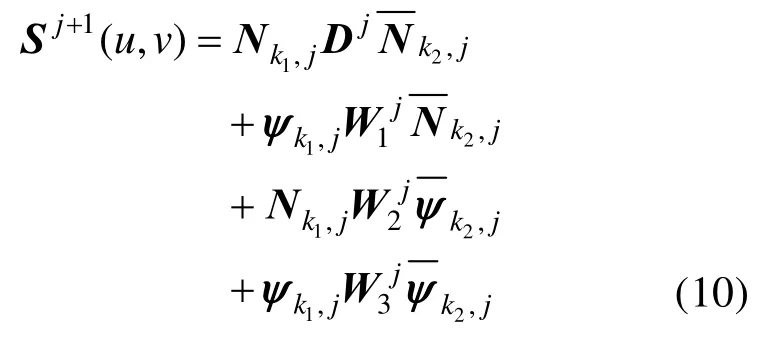
也可以表示为:

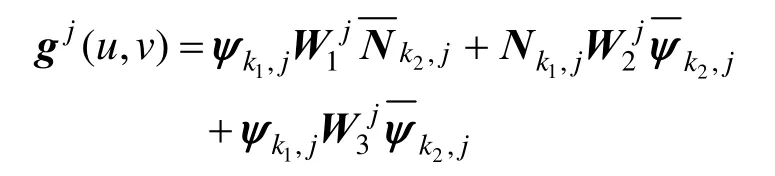
图1给出了多分辨率分解矩阵层次结构关系,反映了在二维张量积标准小波变换形式下NURBS曲面的控制顶点矩阵的多分辨率分解关系。
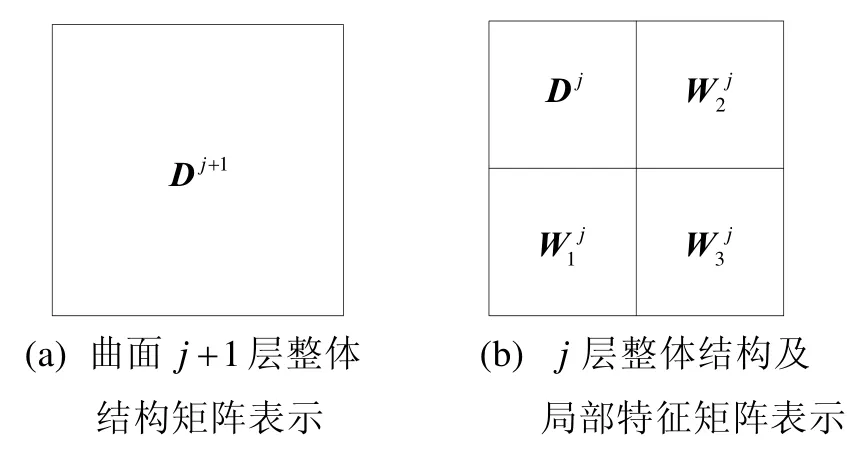
图1 多分辨率NURBS曲面控制顶点矩阵的层次关系
3 曲面自由型特征处理
数据的分析、可视化和处理作为科学工程中的核心内容。数据的形式千差万别,可能是一维参数的函数,也可能是二维参数下的函数,相对于这二者还有比较简单的点序列形式。多分辨率方法的基本思想就是利用一族系数来表示函数,每个系数提供了关于函数的位置和频率的相关信息。函数的小波多分辨率表示包含了结构的全局特征和不同分辨率层下的细节特征。
通过上节内容的分析可知,小波多分辨率技术使NURBS曲面以B样条基函数为基础的数学表示形式被变换到多尺度下的整体结构和局部细节的自由型特征表示形式。对NURBS曲面的编辑和处理就转变为对其曲面自由型特征的编辑和处理。对 NURBS曲面多尺度下的自由型特征的处理主要包含两个方面:其一是指对自由型特征自身的编辑,比如:自由型特征的修改、放大、缩小等等;其二是指自由型特征在不同曲面之间的复制和粘贴。本文主要针对第二个方面进行分析讨论。NURBS曲面自由型特征的复制和粘贴包含两种类型,即曲面之间及曲面自身的特征复制和粘贴。
3.1 曲面之间自由型特征的处理
在不同的 NURBS曲面之间进行特征的多分辨率处理包含如下3个过程:
(1) 曲面特征的复制,即局部特征的提取。令SJ(u, v)为原曲线, DJ为其控制顶点矩阵。如图2所示,通过多分辨率分解,曲面的所有特征信息皆包含在各分辨率层的小波加权系数矩阵中。
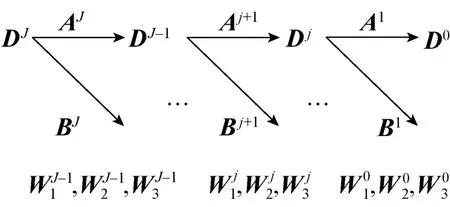
图2 NURBS曲面的特征提取
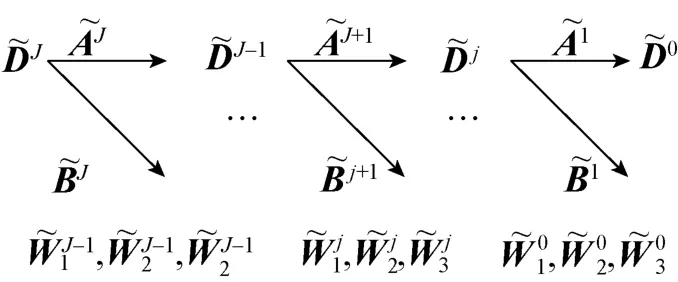
图3 目标曲面的多分辨率分解
(3) 特征的粘贴,是使原曲面与目标曲面的细节特征合并,通过多分辨率重构实现特征在目标曲面上的粘贴,如图4所示。

图4 曲面细节特征的粘贴
经过粘贴后,目标曲面中新的细节特征包含在小波加权系数矩阵之中,随后即可以通过NURBS曲面多分辨率局部特征重构完成曲面细节特征的粘贴。
图5为不同NURBS曲面之间细节特征进行复制和粘贴的实例。从图中可以看出,采用多分辨率分析技术能够有效地实现在 NURBS曲面之间自由型特征的复制和粘贴。

图5 曲面细节特征的复制与粘贴
3.2 曲面自身之间特征的处理
NURBS曲面的细节特征不仅可以在不同的曲面间实现多分辨率的复制和粘贴,也可以在同一曲面上进行。实现过程,包含4个步骤:
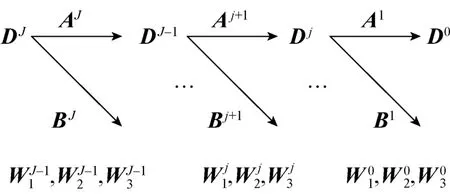
图6 细节特征的提取
(2) 特征重构。将最低分辨率层 D0赋予即将的各个元素都置为零,即令:

图7 曲面特征重构
将步骤(1)得到的各分辨率层中代表整体结构的尺度函数控制顶点矩阵与进行重构,得到,如图8所示。
图8 曲面整体结构重构
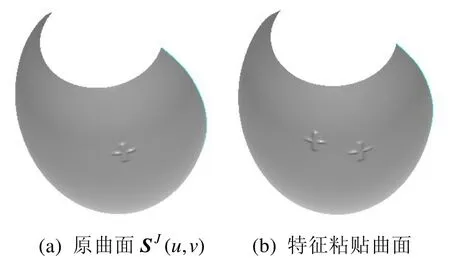
图9 曲面自身特征的复制和粘贴
从 NURBS曲面的自由型特征的处理可以看出,基于多分辨率技术自由型特征的复制和粘贴可以考虑创建一个包含不同自由型特征的NURBS曲面特征库。这些特征可以互换地应用于不同的曲面之中。通过各种不同形式进行特征的获取,比如通过函数所创建的曲面,以及在逆向设计中测量得到的曲面等都可以成为获取特征的来源。而且特征的来源并不仅限于连续的曲面形式,可以扩展到离散点云形式的曲面,或者其他的一些表示形式。
4 结 论
以参数化B样条为基础创建的NURBS曲面在其传统的编辑和处理过程中不但繁琐而且费时,对 NURBS曲面的自由型特征则不能进行有效地处理。小波多分辨率分析技术将单一尺度几何空间 NURBS曲线数学表示形式转化为多尺度空间下的频域表示形式,有效提取了NURBS曲面的整体结构和局部细节信息,并分别将其转换为NURBS曲面的整体与局部自由型特征。文中的实例表明,多尺度自由型特征的获取可实现对其特征的编辑、操作和处理,也有效实现曲面之间以及曲面自身之间特征的编辑和处理。基于自由型特征对 NURBS曲面进行几何建模不仅可以提高其设计的效率、加速产品的概念设计、创新设计等,而且对有效利用企业的信息和知识也具有重要的价值。
[1]Lyche T, Mørken K, Quak E. Theory and algorithms for non-uniform spline wavelets [M]. Multivaritate Approximation and Applications, Cambridge: Cambridge University Press, 2001: 152-187.
[2]刘 建, 关右江, 秦开怀. 任意NUBS曲线的小波分析和造型技术[J]. 中国图象图形学报, 2002, 7(9): 894-900.
[3]Li Denggao, Qin Kaihuai, Sun Hanqiu. Curve modeling with constrained B-spline wavelets [J]. Computer Aided Geometric Design, 2005, 22(1): 45-56.
[4]Bertram M. Single-knot wavelets for non-uniform B-spline [J]. Computer Aided Geometric Design, 2005, 22(9): 849-864.
[5]Pan Rijing, Yao Zhiqiang. Biorthogonal nonuniform B-spline wavelets based on a discrete norm [J]. Computer Aided Geometric Design, 2009, 26(4): 480-496.
[6]李爱民, 方宗德. NURBS曲线曲面的多分辨率几何建模[J]. 计算机辅助设计与图形学学报, 2010, 22(8): 1339-1343.
[7]时 宝, 王兴平, 盖明久. 泛函分析引论及其应用[M].北京: 国防工业出版社, 2006: 185-216.
[8]彭玉华. 小波变换与工程应用[M]. 北京: 科学出版社, 1999: 36-62.
Research on Processing Methods for Free-Form Features of NURBS Surfaces
Li Aimin, Niu Qinyu, Kou Farong, Tian Haibo
(School of Mechanical Engineering, Xi'an University of Science and Technology, Xi'an Shaanxi 710054, China)
Because of imparametrization and no determinate boundary of a NURBS surface with free-form features, representing, editing or operating them is still troublesome. The multi-resolution representation of a NURBS surfaces is realized by a new kind of wavelet multi-resolution analysis technology, and representation of the NURBS surfaces is transformed from single-scale geometric space to multi-scale frequent space. Through wavelet filter banks, the total configurations and local details of models are transformed to total and local multi-resolution free-form features. This makes it easy for editing, operating, and controlling a NURBS surface. This approach not only raises efficiency of the NURBS surface geometric modeling, but also overcomes miscellaneousness and troublesomeness in the conventional modeling.
NURBS surface; free-form feature; B-spline wavelet; multi-resolution analysis
TP 317
A
2095-302X(2015)01-0017-05
2014-03-27;定稿日期:2014-07-02
陕西省教育厅自然科学基金资助项目(11jk0859)
李爱民(1972–),男,河南洛阳人,讲师,博士研究生。主要研究方向为计算机辅助几何设计、计算机图形学、CAD/CAM/CAE等。E-mail:li_aimin@sina.com

