哈萨克族传统建筑文化中的几何元素

木尔扎别克·阿不力卡斯， 吴和敏

(1. 新疆教育学院数学学院，新疆 乌鲁木齐 830043；

2. 新疆教育学院现代教育技术中心，新疆 乌鲁木齐 830043)

哈萨克族传统建筑文化中的几何元素

木尔扎别克·阿不力卡斯1， 吴和敏2

(1. 新疆教育学院数学学院，新疆 乌鲁木齐 830043；

2. 新疆教育学院现代教育技术中心，新疆 乌鲁木齐 830043)

哈萨克族传统建筑文化是少数民族文化的重要组成部分。哈萨克族传统建筑中蕴含的数学思想体现了哈萨克民族的数学智慧。分析归纳了哈萨克族传统建筑中的几何元素、所对应的各种几何图形及其内在联系。对农牧区本土中小学数学课程特有资源的开发和利用有现实意义。

哈萨克族建筑；传统建筑文化；几何元素；本土课程资源

数学课程基础教育的新理念是，学生应能够体会数学与自然及人类社会的密切联系，增进对数学的理解和建立学好数学的信心。数学课程应体现文化、美学、艺术、实用价值，其教学活动必须建立在学生的认知发展水平和已有的知识经验基础之上[1]。目前中小学使用的是国家统编数学教材，对少数民族地区中小学数学教学不太适宜。在现行数学教材中出现的现代化城市建筑，如，上海东方明珠塔的球形、现代化厂房结构、大桥结构与形状为范例讲解相关几何知识；我国西部边远地区少数民族学生对这些建筑非常陌生，教学效果不好。为了让我国农牧区的学生在已有的知识经验基础之上来学习几何，并用日常生活中的知识理解所学的几何知识，增进他们对几何(数学)的兴趣，增强他们学好几何的信心，研究者在哈萨克族传统建筑的结构研究过程中，手绘画图和拍摄了大量哈萨克族传统建筑图片并搜集了相关资料。哈萨克族传统建筑中蕴藏许许多多的几何知识，若把这些知识引用到中小学数学教学中是非常有意义的，这对于新疆、内蒙古等农牧区的学生从日常生活中感受到数学的存在，体验“空间与图形”对当今社会生活的重要作用，有利于培养学生从几何(数学)的角度观察问题、解决问题能力。

1 问题的提出

新疆哈萨克族数学文化是我国数学文化的重要组成部分。新疆哈萨克族的传统建筑，哈萨克族的刺绣、花毡、服饰、家居用品、劳动工具、马鞍用具中蕴含着丰富的数学思想，体现了哈萨克族的数学智慧。目前统编教材缺乏农牧区地域文化特色，与学生实际生活环境严重脱节，诸如课堂教学方式、数学教材的选择太少，教材中的术语、定义(概念)、定理(性质)、公式等的举例与少数民族学生的生活几乎没有联系[2]，这样的教材无法满足少数民族地区多元文化教育的需求[3]。学校的数学课程应充分地尊重学生的生活特征，而且要以某种方式在数学课程中反映和利用这些文化特征，使所有学生都能够从身边的可见的事例理解数学概念和知识，提高他们的数学水平及素质。对于中国这样一个少数民族众多的国家，不同民族的风土人情、文化氛围和教育传统有着很大的差异性。因此，基于民族数学文化的教育观点，农牧区的数学教育要在融合于主流文化的基础上，扎根于本民族文化的土壤。要做到这一点，最为基础的研究就是在充分考虑农牧区学生数学思维、空间思维、认知特点、数学文化背景的基础上，努力实现农牧区中小学本土数学课程特有资源的开发。农牧区的学生对周围的建筑纹饰图案是比较熟悉的，在基础教育的数学课堂上，注重本土数学课程特有资源的开发和利用，结合数学知识、几何图形的欣赏、认识和图形的变换讲授相关数学知识，使数学贴近学生的生活，激发学习数学的兴趣和积极性、提高农牧区学生的数学学习自信心、从进而提高农牧区学生学习数学(几何)的效果。

民族数学文化的意义不仅在于它是民族文化的重要组成部分，最主要的还在于它对中小学数学教育教学的现实作用和价值。我国少数民族的日常生活中隐藏着丰富的数学知识，各种空间几何图形、平面几何图形，即相似形、全等形、轴对称与中心对称、平移、旋转、反射等，结合少数民族数学文化与民族学生实际开展因材施教，促进数学课程内容的改革，开发本土教材，具有现实意义。事实上，每个民族都有自己独特的文化体系，农牧区学校教育的内容要与之紧密结合，才能激发学生的学习兴趣，才能保证民族传统文化的传承。梳理少数民族日常生活中诸多方面所涉及的几何元素，可以看到其文化中蕴藏着有利于少数民族学生进行几何(数学)学习的“直观、生动、有趣”易于理解的民族数学文化资源。这些丰富的自然与人文资源，为本土课程的开发提供了广阔的前景[4]。

2 研究方法

2.1 哈萨克族传统建筑几何元素资料的调查与整理

从几何的视角对哈萨克族传统建筑结构进行探索性研究，通过野外调查、访谈、文献检索等方式搜集与其传统建筑结构几何元素相关的资料。野外调查主要针对现存的哈萨克族传统建筑，拍摄了一些宝贵的建筑实物图片。研究者在多年中，先后赴伊犁、阿勒泰、塔城等地对哈萨克族传统建筑进行了调查与整理。访谈对象包括：哈萨克族建造人员、哈萨克族建筑文化的传承人；收集他们保存的珍贵历史图片、文字资料；记录他们对历史建筑的口头叙述。文献检索自1991年至今已出版的各种版本的民族文献资料，特别将哈萨克族毡房结构的研究经验和方法[5-6]结合在一起进行整理，形成比较完整的哈萨克民族建筑几何元素资料集。

2.2 根据中小学数学教材几何部分内容从哈萨克民族建筑几何元素资料集中选取适合的内容

通过中小学数学教材几何部分的结构内容分析与研究，根据哈萨克民族建筑几何元素资料集，选取相关内容用于少数民族地区中小学几何教学，以求找到有效的教学策略，构建相应教学模式，并在实践的教学中检验、改进。

3 哈萨克族传统建筑中的空间图形

3.1 传统建筑与对应的空间图形

3.1.1 毡房建筑立体图

哈萨克族毡房模型都分别与三维空间中的立体图对应，如图1所示。其中图1(a)是哈萨克族传统大毡房(克谊孜宇——Kiyiz uy)，由不同的4个立体图(从下往上分别为圆柱、球带、圆台、球冠)组成，参见图2；图1(b)是中毡房(霍斯——Hos)，由不同的两个立体图(圆台、球冠)组成；图1(c)是小毡房(乌兰海——Uranhay)，而图1(d)是临时毡房——人字型小窝棚(依塔尔哈——Iytarha)，他们分别与圆锥、三棱柱对应，参见文献[7]。

图1 哈萨克族毡房建筑

图 1(a)是哈萨克族传统大毡房，它的框架(骨架)从下往上栅栏、撑杆(撑椽)、穹庐(顶圈架)三部分组成，图1(b)是中毡房，它的框架从下往上撑杆、穹庐两部分组成，而图1(c)是小毡房，它的框架由若干个撑杆组成，这些不同哈萨克族毡房的地面投影均为圆(圆盘形或若干个同心圆)。图1(d)是临时毡房，它的框架两张或四张栅栏组成，其地面投影是长方形或正方形。该内容在高中数学 2(必修，人教版2008年10月)第一章第1节1.2空间几何体的三视图和直观图的教学中；初中数学九年级上册(人教版2014年6月)第二十四章第3节24.3多边形和圆的教学中；初中数学七年级上册(人教版2014年6月)第四章几何图形初步的教学中和高中数学第三册(选修Ⅱ，2003年 6月)第二章，极限的教学中都可以参考。

哈萨克族大、中、小毡房的地面投影都是圆形(圆盘形)，而临时毡房图1(d)的地面投影是长方形或正方形。大毡房的组装(搭建)比较复杂，围墙由四张或六张木栅栏组成(多用六张木栅栏)，其空间形状为圆柱，六张木栅栏即为圆柱的侧面。在图2(a)中阴影部分的左棱为轴，在三维空间中旋转360°后构成的曲面顺序称为(从下往上)圆柱、球带、圆台、球冠。其中球带是球面在两个平行截面之间的部分；球冠是球面被一个平面截得的一部分。从旋转体的角度去看，大毡房也是空间直角坐标系 xyzo- 中oz轴为对称轴的一种旋转体，叫做“哈萨克毡房形旋转体”。该内容在初中数学七年级上册(人教版2003年12月)第三章第1节3.1.1立体图形的教学中；初中数学九年级上册(人教版2007年5月)第二十四章第1节24.1.1圆的教学和第 4节24.4.2圆锥的侧面积和全面积的教学中；高中数学2(必修，人教版2008年10月)第一章空间几何体的教学中都可以参考。

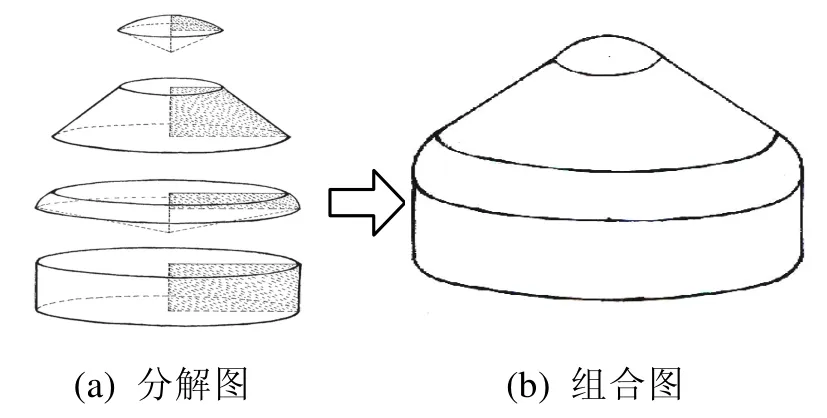
图2 哈萨克族大毡房几何模型

3.1.2 木房建筑立体图

图 3(a)~(c)是哈萨克族传统木房(屋顶似“人”形的木房)，这些木房的下半部分是长方体或正方体，上半部分是三棱柱，这些木房的地面投影为长方形或正方形。图3(c)是保留了传统建筑风格的现代建筑，其由长方体、交叉的三棱柱等几何体组成。

图3 哈萨克族木房建筑

该内容在小学数学一年级上册(人教版 2014年6月)目录4认识图形(一)和小学数学一年级下册(人教版2013年11月)目录1认识图形(二)的教学中都可参考。

3.1.3 土房建筑立体图

图4(a)是伊山赛提清真寺，它由三部分组成，即长方体、圆柱体和上面的球冠，其地面投影为长方形，长方形里面包含圆形。图4(b)是1773年在伊宁市建成的拜吐拉清真寺，它是四层建筑，最上一层是正六棱柱，它的地面投影为长方形，长方形内包含正方形、正方形内包含正六边形，本寺亭由12根柱子支撑，其空间形状为长方体、正四棱柱和正六棱柱的组合；在第二、三层中的四根柱子即为四棱柱的侧棱；在第四层中的六根柱子即为正六棱柱的侧棱。图4(c)是伊宁县其巴尔吐别克清真寺，它由上下两部分组成，即下半部分是长方体、上半部分是楔形，它的地面投影为长方形，长方形内包含两个等腰三角形和两个等腰梯形，其空间形状为长方体和楔形的组合体。它是保留了哈萨克族传统建筑风格的现代建筑。该内容在高中数学第二册(下B，人教版2001年10月第2版)第九章直线、平面、简单几何体的教学中可参考。

图4 哈萨克族土房建筑

3.2 传统建筑中的“点”、“线”、“面”

在中小学《数学》教科书中的几何图形都由“点”、“线”、“面”组成，同样传统建筑中也是如此。比如，哈萨克族传统建筑“毡房”中的木栅栏(围墙)是由“点”、“线”(曲线)组成，圆屋顶是由直线和曲线(撑杆)组成，而穹庐(天窗)是由圆、弧(拱弧)组成；哈萨克族传统木房建筑和土房建筑也由“点”、“线”、“面”形成。如，在建筑中每两个棱或三个棱的交叉处表示一个“点”(或者三个平面的公共交点)、每两面的交叉处表示“直线”。墙面或平面的构成：三个点、相交的两条直线、平行的两条直线、一点和一条直线都构成一个平面。该内容在初中数学七年级上册(人教版2003年12月)第三章第1节3.1.2点、线、面、体的教学中可参考。

3.3 传统建筑中的“曲面”

3.3.1 传统毡房中的曲面

在图1(a)中哈萨克族大毡房的大小是根据木栅栏(房墙)的多少来定，大毡房整套木栅栏的多为偶数，奇数少见。一般的大毡房多用4~6张(块)木栅栏。每张栅栏宽约2.5~3.5 m，高约1.5~1.7 m；如果人口多，经济条件好，可使用 8~10张栅栏，这种大毡房高大而宽敞，被称为宫殿(窝尔达——Orda)。在历史上也有过 12~18张栅栏的大毡房，这种大毡房称为白宫殿、洁白的毡房(阿克窝尔达——Ah orda)；“根据资料，历史上也用过庞大的30张栅栏的大毡房”[8]，这种大毡房称之为金宫殿(阿勒腾窝尔达——Alten orda)。当木栅栏中每一个网格面积无穷小时，该栅栏表示曲面。

大毡房的高度随其大小变化，常用大毡房的高度一般在4~5 m，占地面积20~30 m2，四周是圆柱形的木栅栏(围墙)，顶部由圆屋顶和弓形两个曲面组成。常用哈萨克族大毡房的内壁一般 4~12段交叉的活动木栅栏(可列格——Kerege)做围墙；毡房的圆屋顶由撑杆(乌俄克——Weh)和顶圈架(强俄拉克——Xangerah)构成，其中房顶是顶圈架(天窗)；撑杆上段直，下段60~70 cm处弯曲，木栅上拴接数十至百十根撑杆(撑杆多少，视毡房大小而定)，一般为 60~180根，再将撑杆的另一端插入木制顶圈架的各孔中。哈萨克族大毡房的传统房架从上至下由顶圈架、木撑杆、木栅栏和门(哈语称耶斯克——Esik)等四部分组成，顶圈架位于哈萨克族大、中毡房顶中央。搭建方法：把撑杆的一端插入顶圈架的孔中，其数量与栅栏上端交叉处的叉口数量相等，然后用羊毛绳捆绑，与顶圈架构成一个整体。具有6张木栅栏的哈萨克族传统大毡房盖料一共有7张，即这种房架的外壁盖以 4张毡壁(图尔勒克——Twerleh)，圆屋顶部盖以 2张包毡(吾孜克——Uzik)，房顶部盖以 1张顶毡(屯勒克——Tunglik)。这样构成一个大毡房的整体曲面。该内容在高中数学第三册(选修Ⅱ，人教版2003年6月)第二章极限的教学中可参考。

3.3.2 传统建筑美学依据

哈萨克牧民现居住毡房，经过测量，它的直径=5 m，高度=3.1 m，毡房高度与直径比例约为0.62，其比值是保留前三位数字的近似值为0.618。此比例被称为黄金分割，这个比值称为黄金分割比(中外比)。因为所以黄金分割数是无理数，哈萨克族大毡房构建比例符合黄金分割比，因此看起来显得非常美观庄严。

3.4 空间中的对称

空间轴对称：因为哈萨克族传统建筑的主体形状有圆柱、圆锥、三棱柱、长方体、正方体，所以它们无论属于哪一类建筑都是空间轴对称的。如果将建筑地面投影中心假设为三维空间坐标系o xyz- 的原点，那么oz轴为空间对称轴。 该内容在初中数学八年级上册(人教版2014年6月)第十三章轴对称图形的教学中可参考。

4 哈萨克族传统建筑的对称轴截面图

4.1 平面上的对称

4.1.1 毡房建筑的对称轴截面图和其他平面图

从图2可知，哈萨克族大、中、小毡房在三维空间坐标系o xyz- 中是轴对称房屋。图5(a)是哈萨克族大毡房模型，以oz为对称轴的截面示意图，它的左半部分和右半部分相等，其中包括两个等面积的矩形、三个曲边梯形、一个等腰梯形、等面积的两个直角梯形和弓形等图形，它说明哈萨克族大毡房是空间轴对称房屋。图5(b)是大毡房两扇木门平面示意图，它也是轴对称。图5(c)为哈萨克族大毡房几何模型对称轴截面(平面)示意图，它包括长方形(矩形)、曲边梯形、等腰梯形、弓形等几何图形。当垂直于对称轴的平面相截毡房模型时，出现无限多个不同圆或相似圆。图5(d)是哈萨克族大毡房的木栅栏，在图中伸展木栅栏的格子(网眼)类似于平面上的菱形或平行四边形。该内容在小学数学四年级上册(人教版2011年6月新疆)目录 4平行四边形和梯形的教学中；初中数学八年级上册(人教版2014年6月)第十三章轴对称图形的教学中都可参考。

4.1.2 土房建筑的对称轴截面图

图4是哈萨克族土房建筑，系轴对称房屋。图6是哈萨克族土房建筑以oz为对称轴截面示意图，其左、右部分相等，说明哈萨克族土房建筑是空间轴对称房屋。图6(a)包括长方形、弓形或半圆形、正方形等几何图形；图6 (b)包括长方形(矩形)、正方形、三角形等几何图形；图 6(c)包括长方形、梯形、三角形等几何图形。当垂直于对称轴的平面相截该建筑模型时，出现无限多个不同长方形、正方形、圆、半圆、正六边形等平面几何图形。该内容在小学数学三年级上册(人教版2014年6月)目录7长方形和正方形的教学中；初中数学八年级上册(人教版2014年6月)第十三章轴对称的教学中都可参考。

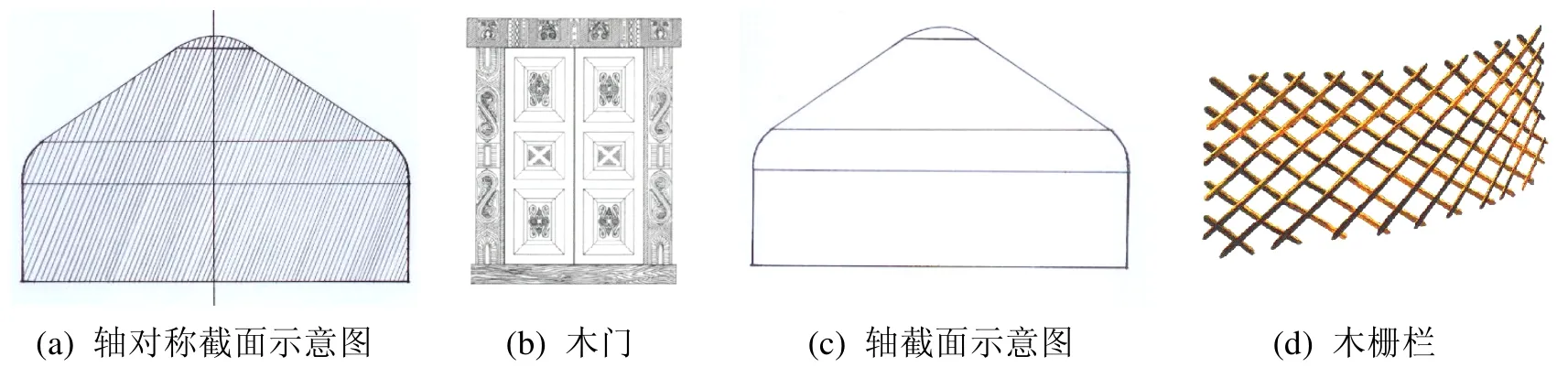
图5 哈萨克族毡房的对称轴截面图和其他图

图6 土房建筑的对称轴截面图

4.1.3 中心对称

哈萨克族传统建筑中的门、窗、地面投影、墙面的平面，当垂直于对称轴的平面相截于该建筑模型时得到的平面图都是中心对称图。该内容在初中数学九年级上册(人教版2014年6月)第二十三章，23.2中心对称的教学中可参考。

4.2 几何变换

平面图形的构造方式也有初等几何的相似变换。初等几何的全等变换，包括轴反射变换、平移变换、旋转变换，平移变换又有共点平移、共线平移、等距离平移。图5(a)和图6(a)~(c)中的几何图形的构成方式是初等几何全等变换中的轴反射变换。图5(b)中的几何图形的构成方式是初等几何变换中的平移变换；而图5(d)是大毡房木栅栏示意图，它是由菱形共点平移或共线平移或等距离平移等变换得到的。其他木房和土房传统建筑对称轴截面图的构成方式是类似的，在这些平面图形中，图形的轴反射、旋转、平移等变换构成了哈萨克族传统建筑形状的整体美与对称美。

5 结 束 语

古代建筑师们在他们漫长的生活经验中反复体验掌握并学到了做各种建筑技术和方法，最早游牧部落做毡房木架的工匠人，定居部落做土房的工匠都凭自己的想象，这说明古代的工匠们能够脱离具体形的实体，已有了不少抽象的几何图形概念，由此才能熟练地做出不同的含有几何图形的建筑来。

哈萨克民族在长期的生活劳动实践中，尤其是在传统建筑的建造中无形地积累沉淀了丰富的数学科学元素，从几何学的角度去审视、解读其传统建筑的建造发现，其中属于空间的有：长方体、正方体、圆柱、圆锥、正棱锥、圆台、球带、球冠、半球体、球台、三棱柱、正棱柱、正六棱柱、楔形和球体；属于平面的有：正方形、长方形、圆形、菱形、梯形、三角形、弓形、平行四边形、半圆形、扇形、椭圆形、圆环、部分圆环和新月形等几何图形。这些图形说明了哈萨克族赖以生存的居所，不仅实用、美观、结实，其中最主要的是传统建筑的建造符合了数学和物理学的科学规律。

本研究为开发国家数学课程和本土数学文化课程资源提供了有益的思路和宝贵资料。任何一个民族都有自身的数学文化，这是数学教育的出发点，也是落脚点，是学生认识数学思维特点的依据，是学校数学教学必不可少的背景材料。少数民族数学文化的意义不仅在于它是民族文化的重要组成部分，最主要的还在于它的现实作用和教育价值。少数民族数学文化在现实的应用和学生的智力开发中具有重要的价值和作用，诸如激发学生学习的自信心、有利于结合少数民族学生实际因材施教、促进少数民族学生整体的和谐发展和个性完善(完美)，强化民族自豪感、自信心及归属意识等[9]。通过充分挖掘少数民族数学文化课程资源，努力开发和研制出多元数学课程资源是提升少数民族地区数学教育质量的重要途径之一。从而体现少数民族建筑、刺绣、花毡、服饰等文物中的数学文化的教育价值，有待于数学教育研究者开展进一步的研究。

[1]全日制义务教育《数学课程标准》(实验稿)[M]. 北京: 北京师范大学出版社, 2003: 1-2.

[2]刘 超, 张 茜, 陆书环. 基于民族数学的少数民族数学教育探析[J]. 数学教育学报, 2012, 21(5): 20-21.

[3]阿力木·阿不力克木. 多元文化整合数学教育理论[J].数学教育学报, 2010, 19(5): 30-33.

[4]申玉红, 杨启祥, 周长军. 少数民族数学文化与中小学数学课程开发[J]. 西南农业大学学报: 社会科学版, 2012, 10(6): 242-244.

[5]木尔扎别克·阿不力卡斯. 哈萨克毡房的几何结构[J].中国民族杂志(哈文), 2012, (5): 11-12.

[6]木尔扎别克·阿不力卡斯. 哈萨克毡房及其几何体结构[J]. 伊犁师范学院学报: 社会科学版, 2008, (2): 22-25.

[7]木尔扎别克·阿不力卡斯.《哈萨克毡房结构及特征》(哈文)[M]. 乌鲁木齐: 新疆青少年出版社, 2014: 254-255.

[8]波拉提·科尔拜耶夫.《哈萨克族建筑艺术》(哈文)[M].奎屯: 伊犁人民出版社, 2006: 40-44.

[9]申玉红, 杨启祥, 周长军. 云南德宏傣族服饰中的数学文化[J]. 数学教育学报, 2013, 22(1): 66-68.

Geometric Elements in Kazakh Traditional Architectural Culture

Muerzhabieke·Abulikasi1, Wu Hemin2
(1. School of Mathematics, Xinjiang Education Institute, Urumqi Xinjiang 830043, China; 2. The Modern Educational Technology Center, Xinjiang Education Institute, Urumqi Xinjiang 830043, China)

Kazakh traditional architectural culture plays an important role in ethnic minority culture. Kazakh traditional architecture embodies wisdom in mathematics. The geometric elements in architectural culture and the corresponding geometry figures as well as their inner correlations have been explored and analyzed in this paper. The obtained results are of great realistic significance in developing mathematics curriculum resources for primary and middle schools in the area where ethnic minority people gather.

Kazakh construction; traditional architectural culture; geometric elements; local curriculum resources

G 750

A

2095-302X(2015)01-0001-06

2014-07-03；定稿日期：2014-08-05

国家自然科学基金资助项目(11361061)

木尔扎别克·阿不力卡斯(1956–)，男，新疆伊犁人，副教授，本科。主要研究方向为数学教育、少数民族文化数字化研究。E-mail：sxmuzha@xjei.cn