三维模型有向三角面片链码压缩方法

刘尚武，魏 巍,3，段晓东，刘勇奎

三维模型有向三角面片链码压缩方法

刘尚武1,2，魏 巍1,2,3，段晓东1,2，刘勇奎1

(1. 大连民族大学计算机科学与工程学院，辽宁 大连 116600； 2.大连民族大学大连市民族文化数字技术重点实验室，辽宁 大连 116600； 3. 大连海事大学信息科学技术学院，辽宁 大连 116026)

首先提出一种适用于三角面片链码算法的改进MC规格化方法，使用单位为2的体素作为改进MC算法中的单位体素，并使用其中的27个顶点重新构建等值面，最终获取高质量的规格化三角网格模型。在新的规格化模型上提出一种新的面片遍历方式，在三角面片链码算法的基础上，采用优先遍历右连接面片原则，控制面片的遍历方向，该方法能够减少面片遍历次数，并且延长面片链码的平均长度。实验结果表明，采用新的规格化方法和新的遍历方法，压缩效果与原三角面片链码相比，具有明显的提升。

面片链码；三维模型；体素；规格化

如今，三维模型被广泛地应用于各行业中。随着计算机硬件的发展，尤其是图形计算及显示能力的提高，图形工作者为了追求高质量的三维模型，不断提高三维模型的精度，从而增加了模型的数据量。例如：使用激光扫描仪得到的高精度稠密点云模型；为了追求高逼真纹理贴图而构建的稠密网格模型；以及通过多幅图像拼接融合构建的大场景三维模型等。其中最为基本的是模型的顶点数量以及面片数量的增加。高精度的三维模型在视觉上具有很好的表示效果，但在非图形处理的普通计算机中，仍受到处理器性能、存储空间以及传输速度等限制。

为了减少三维模型的存储空间，研究人员在三维模型数据压缩技术上做了大量的研究。其中一个研究方向是用链码技术对三维模型数据进行压缩。比如经典的FREEMAN[1]链码。其首次提出用链码表示三维数字曲线，在三维空间中，把链码结构在体素上量化，每个体素圴有26个方向，以此构建三维模型的体素节点，该方法也被称为F26链码。之后，链码技术被广泛地应用于三维模型的表示。BRIBIESCA[2]提出用基于正交方向的二进制链码技术来表示三维曲线。在正交的2个线段上，仅用0和1两个二进制编码来表示下一个正交线段方向，以此类推用二进制编码序列表示三维曲线。SÁNCHEZ-CRUZ等[3]提出一种三维相对链码，由参考向量、支持向量和变化方向向量组成，该方法在26个连通分量的三维体素中搜索相对变化，得到有向最简路径。

链码技术不仅在三维曲线的表示上有着较好的效果，在三维模型表面的表示中同样表现优异。ROSSIGNAC[4]提出的Edgebreaker算法是较早的拓扑压缩算法之一，该算法使用了链码压缩的思想。其原理是在遍历模型网格过程中，始终维持一个有向边界，用于区分已遍历面片和未遍历面片，用5个标识符记录当前遍历面片与边界的关系，得到面片的遍历顺序，最终使用Huffman编码得到压缩效果。文献[5-7]是对Edgebreaker算法的改进，在提高压缩效率的同时，保留了链码技术的思想。LEMUS等[8]提出一种表示三维模型表面的链码方法，并定义了9个方向的变化，对每个方向赋予一个码值，可用一条链码表示全封闭三维模型。该方法可用于表示任何全封闭模型的体素化表面。魏巍等[9]提出了三角面片链码算法，其在基于体素规格化面片的基础上，定义了13种连接边，用连接边和面片第三点的位置来表示三角面片，并对此编码。由于链码本身的平移不变形和旋转不变性，在表示三维模型时不会破环其原有拓扑结构，并能够完整地还原三维曲线或三维模型。以上研究成果均体现了其优点。

本文提出一种用于三角面片链码算法的三维模型重构方法。同时在参考文献[9]三角面片链码算法的基础上，提出一种新的三角网格遍历方法，有向三角面片链码。在模型规格化算法(marching cubes，MC)[10]的基础上进行改进，通过改变体素单位长度，以及重新定义MC算法中的等值面，获得可用于三角面片链码算法的规格化模型。在数据压缩时，通过控制三角面片的遍历方向，增加三角面片链的平均长度，从而减少面片链的数量，对三角面片链进行编码，实现三维模型的数据压缩。该方法能有效地减少整个三维模型的码值数。通过对多个三维模型进行测试，该方法在三角面片链码算法的基础上进一步提高了三维模型压缩效率，表现效果较好。

1 三维模型规格化表示

1.1 MC规格化算法

三维模型表面多用三角网格来表示。其仅包含点、边、面3种基本信息，因此具有良好的拓扑结构。在三维模型不同精度的区域，均可使用大小不同的三角网格表示。如在较为平坦的模型表面，可使用相对较大的三角面片表示，而对于变化复杂的模型表面，可使用多个小三角面片表示。这样的表示方式能够很好地保留模型的原始模样，但由于三角面片大小不一，毫无规律可循，难以进行数据压缩。因此，对于三维网格模型，需要将其进行基于体素的规格化切分。

目前，已有很多对三维网格模型规格化进行研究，并提出了多种规格化算法[11-13]。其中，MC算法是基于体素的三维模型表面规格化较为经典算法之一，其主要思想是在单位体素中寻找一个等值面将模型和外界进行分隔，并用这样的等值面重新表示三维模型表面。图1为参考文献[14]中作者Lorensen给出的15种基本等值面。

在MC算法中，等值面是由单位体素中棱长上选择的点构成，并非由体素顶点构成，此外，面片顶点的选择是由该条棱长上2个端点的权重决定的，因此其位置是不固定的。由此获得的三角面片，没有统一的标准，不适用于三角面片链码算法。

1.2 改进的MC算法

MC算法中体素的单位为1，为了获得由体素顶点构成的三角面片，将8个单位为1的体素合并成一个单位为2的体素，同时保留8个体素中的所有顶点，如图2所示。在这样一个单位为2的体素中，共有27个顶点，将顶点编号为1，3，7，9，19，21，25，27的顶点作为状态点，即这8个点有2种状态：在模型内部和模型外部，剩下的19个顶点为等值面的构造点。

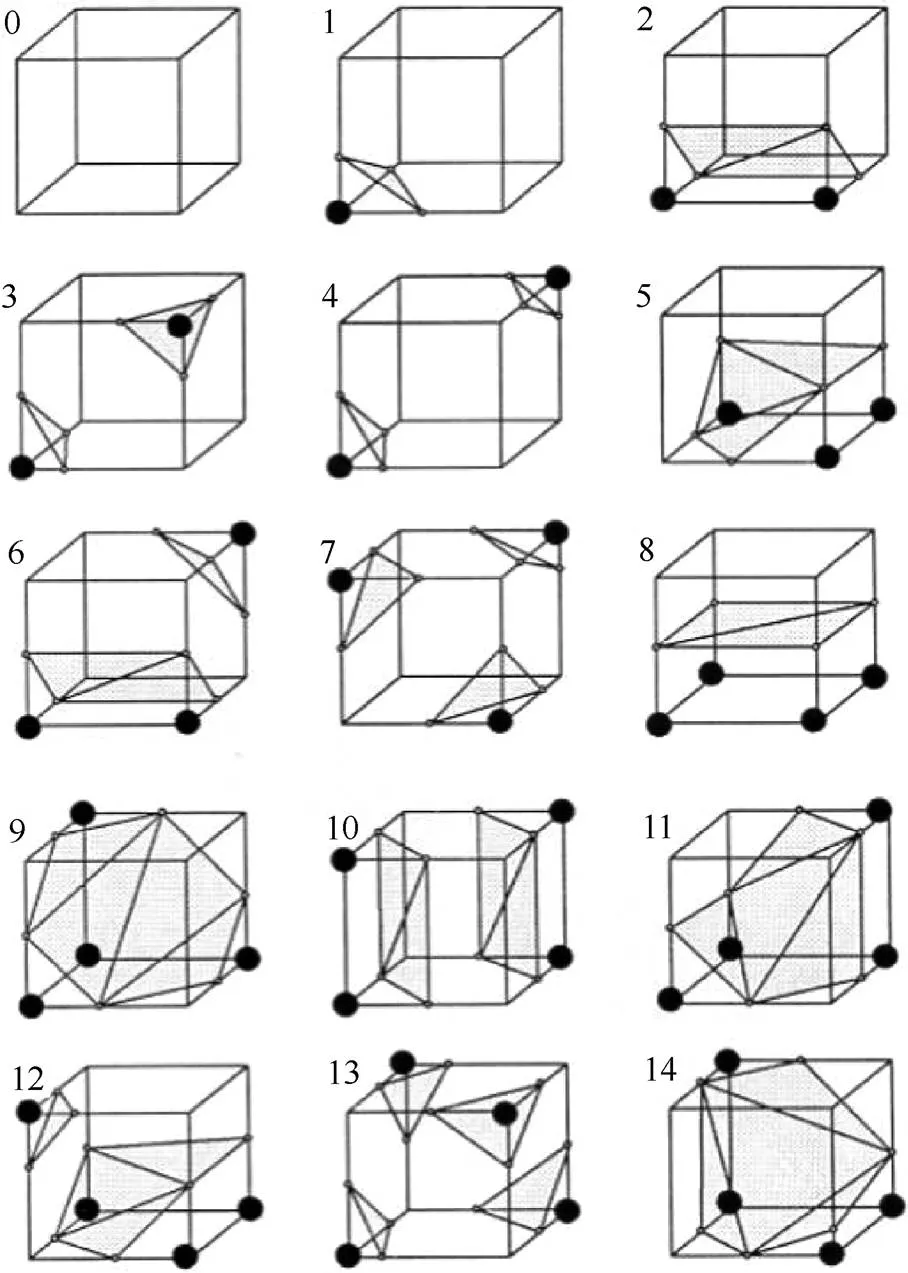
图1 文献[14]中15种基本等值面

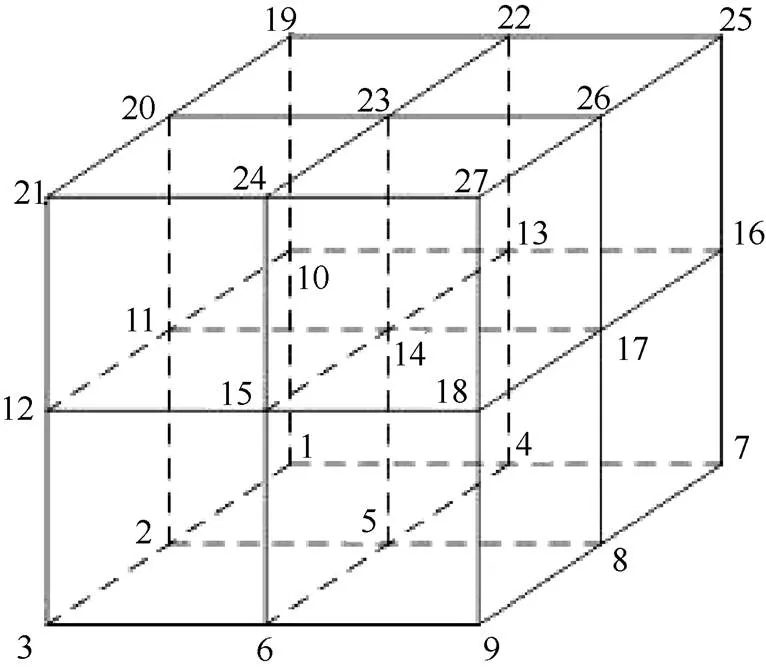
图2 由8个单位为1的体素合并的体素

在MC算法中，等值面的构造点位于体素两端同时有实点(在模型内部)和虚点(在模型外部)的棱长上，在单位为2的体素中构造等值面，同样运用这种思想。如图3所示，顶点19为实点，顶点25为虚点，因此在棱长1925上，选择22作为等值面的构造点。同样，顶点20，2，6，18和16也被选择为等值面的构造点。此外，为了保证规格化三角面片是由单位体素顶点构成，单个等值面的顶点必须在同一体素内。此时，顶点14是唯一一个被8个单位体素共用的顶点，因此复杂等值面的三角面片可以经过顶点14来构造。在图3中，新的等值面一共由8个三角面片组成，每个面片均是由单位体素的顶点构成。

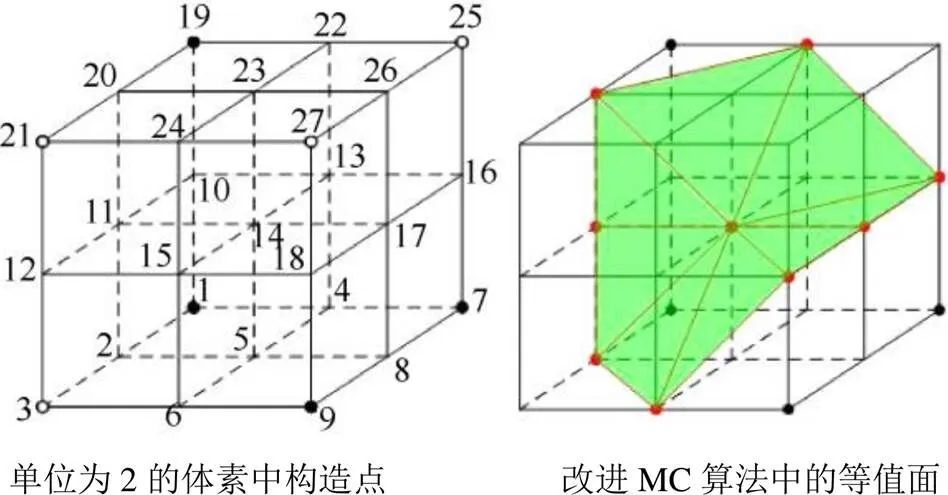
图3 单位为2的体素中构建等值面

图4给出了原始MC算法和改进MC算法在同一种情况下构造的等值面。与原始MC算法相比，改进MC算法在构造等值面点集的选择上做了变化，不仅选择了两端分别为实点和虚点的棱长上的点，同时也选择了体素面的中点，以及体素内部中点作为等值面的构造点。改进的MC算法保留了选择等值面构造点的思想，同时利用单位体素顶点，将等值面中的三角面片限制在单位体素内，每个三角面片都由单位体素的顶点构成，这样的三角面片与面片链码中的三角面片相同，因此，改进MC算法所生成的规格化模型可以使用面片链码进行压缩。同时，改进的MC算法只对原始MC算法中等值面的构造方法做了改动，并不影响原始MC算法生成高质量三维网格模型的特点，因此由改进MC算法对三维网格模型进行规格化表示，能够获得更好的规格化模型。

图4 原始MC算法与改进的MC算法构造等值面对比

在改进MC算法中，对每一种等值面类型均进行了重新定义，图5给出了改进MC算法中15种基本等值面构造方法，与MC算法相同，剩余的所有等值面类型均由这15种基本类型组合而成。

图5 改进MC算法中15种基本等值面

1.3 改进MC算法规格化效果

在算法实现过程中，使用文献[14]的优化方法进行编码，以提高程序的效率。通过对Armadillo，Bunny，Happy Buddha，Panther和Santa模型进行测试，得到的改进规格化模型如图6所示。其中，原规格化方法为文献[9]的方法。从图6中可以看出，对于三角面片链码规格化方法，改进MC算法所获得的规格化模型更为平滑，面片更为规律。在文献[9]的三角面片链码算法中，三角面片在模型表面的表现是影响压缩效果的一个重要因素。当模型表面不够平整，毫无规律，易出现几个面片构成的闭环，形成较短的面片链，进而影响模型的压缩程度。而当模型表面较为平滑时，就可减少短链出现的概率。同时，在Meshlab软件上对三维模型进行检测，使用改进MC算法获得的规格化模型均具有，没有缝隙、没有孔洞、没有相交面片和非流形边的高质量特点，可见改进MC算法在直观上具有较好的重建效果。

在三维模型中，一个极为重要的指标是模型重建误差。本文采用单向Hausdorff距离测量改进MC算法的误差值。Hausdorff距离是HUTTENLOCHER等[15]在1993年提出的图像对比算法，即测量2个点集的匹配程度。对于点集的每一个点，Hausdorff距离计算了与点集中最近点的距离，并取最大距离值作为2个点集的误差值。对于2个不同的点集，Hausdorff距离能够准确地度量其在空间上的匹配程度，是非常实用的误差计算方法。由于规格化模型与原始模型的顶点数量差异过大，因此采用单向Hausdorff距离作为判断标准。

以Bunny模型为例，表1给出了1万~10万不同面片数量级的单向Hausdorff距离。从表中可以看出，对于不同面片数量的规格化模型，其误差均在0.100 0以下。同时，文献[9]中规格化方法的平均误差为0.024 2，改进MC算法的平均误差为0.033 1。在Hausdorff距离评判标准中，临界值为0.100 0，即重建误差小于0.100 0时，重建效果可被接受。因此，改进MC算法的模型重建误差虽然比文献[9]方法要大一些，但仍然在接受范围之内，所以同样有着较好的重建效果。

图6 改进MC规格化算法与原规格化算法效果((a) Armadillo原始模型；(b) Bunny原始模型；(c) Happy原始模型；(d) Panther原始模型；(e) Santa原始模型；(1)~(3)改进MC算法3万、5万、10万面片；(4)~(6)原规格化方法3万、5万、10万面片)

此外，表1中还给出了体素单位为2的情况下使用原始MC算法得到重建模型的误差值略高于改进MC算法，但两者相差并不大。其差异来源于2种算法重建模型的顶点数量不同以及单向Hausdorff距离的计算方式。通过对比图1和图5可以看出，改进MC算法提取的等值面数量和顶点数量要多于原始MC算法。在体素单位为2的情况下，原始MC算法将体素作为一个整体进行等值面的提取，而改进MC算法是通过8个单位为1的体素合并为单位为2的体素，虽然操作体素的单位为2，但等值面的构建是在单位为1的体素中完成，因此改进MC算法重构的模型有更多的顶点。Hausdorff距离是计算2个点集之间最近点的最大距离，当重建模型的顶点数量更多时，最近点的距离也会相对减小。因此原始MC算法的误差值会略大于改进MC算法。

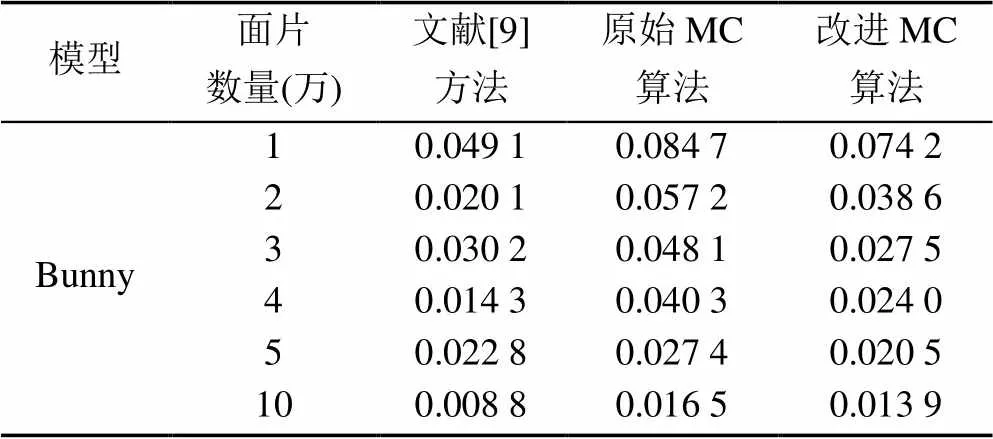
表1 改进MC算法、原始MC算法和文献[9]方法单向Hausdorff距离

通过图7可以发现，Bunny模型中的重建误差值，随着面片数量的增多逐步减小。可以预见，当模型达到一定精细程度时，由于面片数量足够多，以至于可以忽略模型重建的误差。但是，这种现象并不适用于所有模型，比如图8中Santa模型的误差数据，虽然其误差也是随着面片数量的增多而逐步减小，但效果却并不明显。

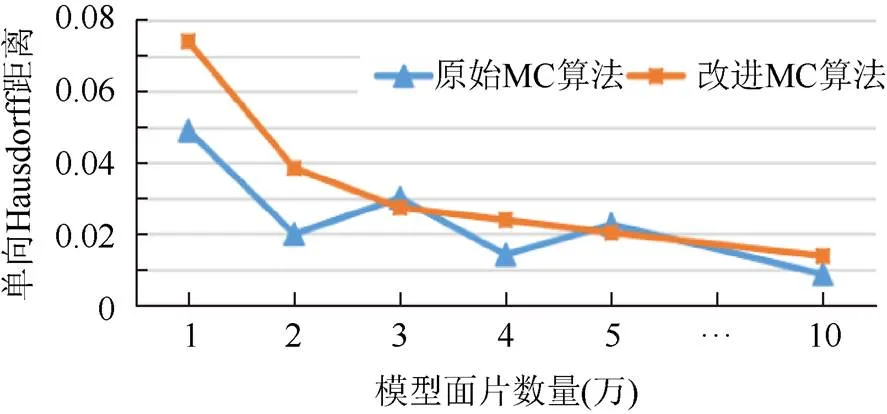
图7 Bunny模型单向Hausdorff距离趋势

图8 Santa模型单向Hausdorff距离趋势

2 有向三角面片链码表示三维模型

2.1 有向三角面片链码主要思想

在文献[9]的三角面片链码算法中，为了能够完整表示三维网格模型，采用了双向分层的遍历方法。首先在三维空间坐标系中选取一个坐标轴方向，对整个模型进行分层遍历，再选取另外一个坐标轴方向，进行分层遍历。这种遍历方式能够规则地构造面片链，并有效控制其数量，但存在部分相同的三角面片会同时被2个方向的分层遍历的问题，由此造成数据冗余，而且随着模型规模的增长，重复遍历的面片数量会随之增多，使得采用该算法压缩的文件会显著增高。因此，在新的面片链码算法中，如何减少三角面片遍历数量是算法改进的主要思路。

三角面片包含3条边和3个顶点。在三维网格模型中，1条边仅被2个三角面片共用，这个特性保证了三角面片之间连接的唯一性。假设一个三角面片与上一个面片连接的边为入边，与下一个连接的边为出边，与入边或出边连接的，必定有且仅有一个三角面片。该特点适用于规格化模型中的所有三角面片，从一个三角面片开始，确定其入边后，选取该面片另外2条边中的任意一条作为出边，便能使用面片链码算法中的定义将2个面片连接在一起。分层遍历是为了将面片遍历维持在同一层，且从遍历开始到结束都有着固定的方向，其束缚了面片遍历的选择性。因此，在新的面片遍历方法中，要舍弃双向分层遍历的思想，保证每个面片只遍历一次，消除三维网格模型数据压缩时的数据冗余。

若是在无约束的情况下，随机遍历三角面片，将会造成不可控的结果。最好的结果是所有面片在一条面片链上，最坏的结果是面片链成环状，包围着一个三角面片，被包围的一个三角面片需要单独成链。这种对面片链的长度无法预知的情况是不理想的。因此，在遍历三角面片时需要给定一个遍历方向，让面片遍历变的可控，即有向三角面片链码。如图9所示，遍历三角面片，设1是第一个面片，任意选取12作为入边，则13和23中的任意一条边可被选择为1的出边。设顶点1为面片1的第一顶点，2和3分别为第二、第三顶点，根据面片顶点的相对位置，1的右出边为23，左出边为13。在遍历1时，优先选择与23相连接的三角面片作为下一个遍历面片，即优先选择右连接面片，若与23连接的三角面片已经被遍历，则选择与13连接的三角面片，若其同样被遍历，则1为当前面片链的最后一个面片。

图9 有向三角面片链码算法

在遍历每一个三角面片时均选择优先遍历右连接面片原则，三角面片链的遍历路径为螺旋状向外延伸。图10为有向三角面片链码遍历路径。

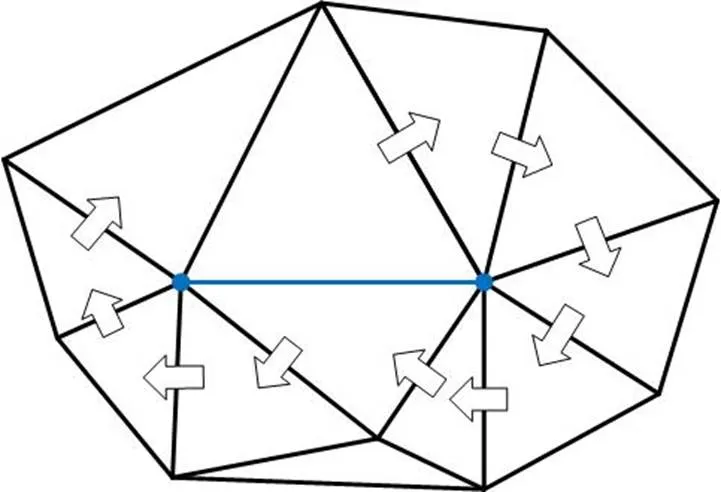
图10 有向三角面片链码遍历路径

有向三角面片链码遍历三角面片有2个优点：①按照螺旋状向外延伸的遍历路径，可以紧密的遍历三角面片，在已遍历的区域不会出现被面片链包围的面片，减少了单个面片或少数面片成链，即短链出现的概率；②与分层遍历相比，分层遍历仅能遍历属于当前层的三角面片，而有向三角面片链码在遍历时没有该限制，只要有连接的面片，便可以一直遍历下去，因此有向三角面片链码构造的面片链的平均长度要比分层遍历的平均长度更长。同时有向三角面片链码对每个三角面片只遍历一次，降低了大量的数据冗余。

2.2 有向三角面片链码算法

有向三角面片链码算法是新的面片遍历方法，因此沿用三角面片链码算法中的数据结构定义，同时也沿用了对原始三维网格模型的预处理过程，详细过程参考文献[9]。有向三角面片链码算法流程具体如下：

输入：规格化三维网格模型面片数据。

输出：有向三角面片链码算法编码。

步骤1.模型首个面片读取与编码。

步骤1.1.随机选取一个遍历标志位为0(未遍历)的三角面片1，将其遍历标志置为1，按默认顺序将该面片的3个顶点记为1_1，1_2，1_3。

步骤1.2.计算1_2到1_1的相对位置，在连接边定义表中查找或-，确定1的连接边类型1_i。若查到，则将1_1，1_2互换。

步骤1.3.计算1_3到1_1的相对位置，在1_i下三角面片定义表中查找，确定1的面片编码。

步骤2. 构建一条有向三角面片链码编码。

步骤2.1.在未遍历面片中寻找与1_21_3连接的三角面片。若找到，执行步骤2.2，否则，执行步骤2.3。

步骤2.2.将连接面片记为2，将2中与1_3相等的点记为2_1，与1_2相等的点记为2_2，第3点记为2_3，并将1数据结构中连接边标识位置0。执行步骤2.5。

步骤2.3.在所有未遍历面片中寻找与1_11_3连接的三角面片。若找到，执行步骤2.4，否则，执行步骤2.9。

步骤2.4. 记连接面片为2，将2中与1_1相等的点记为2_1，与1_3相等的点记为2_2，第3点记为2_3，并将1数据结构中连接边标识位置1。

步骤2.5.将2的遍历标志位置1。

步骤2.6.计算2_2到2_1的相对位置，在连接边定义表中查找或，确定2的连接边类型2若查到，则将2_1，2_2互换。

步骤2.7.计算2_3到2_1的相对位置，在e下三角面片定义表中查找，确定2数据结构中的面片编码。

步骤2.8.将2记为1，重复步骤2.1至步骤2.7。

步骤2.9. 将1数据结构中连接边标识位置0，完成一条有向三角面片链码编码的构建。

步骤3. 重复步骤1至步骤2，直至遍历三维模型所有面片，构建整个模型的有向三角面片链码编码。

2.3 实验与分析

根据上述算法，选取三维模型Armadillo，Bunny，Satan，Panther和Happy Buddha为例，分别统计了各模型1~5万面片的具体规格化面片数量，以及分别使用三角面片链码算法和有向面片链码算法的具体情况，包括模型压缩后的存储空间和压缩率，见表2。需要注意的是，表2中三角面片链码算法的面片个数是去除掉重复面片后的计数。此外，压缩率的计算是由规格化后与压缩后的模型文件计算得出，这是因为规格化模型的面片数量和顶点数量与原始模型不同。

从表2中可以看出，当面片数为1万时，除了Armadillo模型，其他模型的三角面片链码算法压缩效果要比有向三角面片链码算法效果好。对于5个模型，1万面片的三角面片链码算法平均压缩率为98.11%，而有向三角面片链码算法的平均压缩率为97.11%。随着面片数量的增多，有向面片链码算法的压缩率要普遍高于三角面片链码算法。对于2~5万面片的模型，三角面片链码算法的平均压缩率分别为97.07%，95.90%，94.44%和93.19%，有向面片链码算法的平均压缩率分别为97.26%，97.33%，97.38%和97.41%。可以看出，三角面片链码算法的压缩率会随着面片数量的增加而降低，而有向面片链码算法能够维持在一个较高水平的压缩效果。因此当模型的精细程度较高时，有向三角面片链码算法要比三角面片链码算法有着绝对的优势。

表2 三角面片链码算法(文献[9]算法)和有向三角面片链码算法(本文算法)压缩效果

此外，通过对比同一个模型不同面片数量的压缩率能够发现，有向三角面片链码算法的压缩率随着面片数量的增多，不仅能够维持在较高的水平，并且还能以微小的差距逐步提高。例如Bunny模型，1~5万面片的压缩率分别为97.14%，97.32%，97.42%，97.43%和97.44%，5万面片压缩率比1万面片高出0.30%。图12显示了5个模型的有向面片链码算法压缩率，从图中可以看出，5个模型的压缩率与面片数量均为正比关系。其中5万面片压缩率比1万面片分别高出0.28%，0.30%，0.25%，0.17%和0.40%。图11显示了三角面片链码算法，其压缩率与面片数量均为反比关系，且压缩率的下降幅度较大，5个模型5万面片压缩率比1万面片分别低0.53%，6.94%，5.41%，6.91%和4.81%。相比之下，对于规格化面片数量越多的模型，有向面片链码算法能够有更好的压缩效果。

图11 三角面片链码压缩率趋势

图12 有向三角面片压缩率趋势

3 结束语

本文首先提出了改进MC规格化算法，通过重新定义MC算法中的体素大小，以及重新构建等值面，获得可适用于三角面片链码算法，高质量的规格化三角网格模型。并在此基础上，提出三角面片链码算法的改进方法，有向三角面片链码算法。通过控制三角面片的遍历方向，采用优先遍历右连接面片原则，实现三维网格模型数据压缩效率的提高。通过对多个模型实验，证明本文算法具有更好的模型数据压缩效果。但如何将三维模型的如法向量、颜色、材质和纹理信息等信息加入到有向三维面片链码方法中，实现多方位的模型压缩是今后的一个研究方向；另如何提高算法运行效率，也是需要优化的问题之一。

[1] FREEMAN H. Computer processing of line-drawing images[J]. ACM Computing Surveys, 1974, 6(1): 57-97.

[2] BRIBIESCA E. 3D-curve representation by means of a binary chain code[J]. Mathematical and Computer Modelling, 2004, 40(3-4): 285-295.

[3] SÁNCHEZ-CRUZ H, LÓPEZ-VALDEZ H H, CUEVAS F J. A new relative chain code in 3D[J]. Pattern Recognition, 2014, 47(2): 769-788.

[4] ROSSIGNAC J. Edgebreaker: connectivity compression for triangle meshes[J]. IEEE Transactions on Visualization and Computer Graphics, 1999, 5(1): 47-61.

[5] ISENBURG M, SNOEYINK J. Spirale Reversi: Reverse decoding of the Edgebreaker encoding[J]. Computational Geometry, 2001, 20(1-2): 39-52.

[6] JONG B S, YANG W H, TSENG J L, et al. An efficient connectivity compression for triangular meshes[C]// Proceedings of Fourth Annual ACIS International Conference on Computer and Information Science (ICIS’05). New York: IEEE Press, 2005: 583-588.

[7] 刘迎, 刘学慧, 吴恩华. 基于模版的三角网格拓扑压缩[J]. 计算机辅助设计与图形学学报, 2007, 19(6): 703-707. LIU Y, LIU X H, WU E H. An mode-based connectivity compression for triangular meshes[J]. Journal of Computer-Aided Design & Computer Graphics, 2007, 19(6): 703-707 (in Chinese).

[8] LEMUS E, BRIBIESCA E, GARDUÑO E. Representation of enclosing surfaces from simple voxelized objects by means of a chain code[J]. Pattern Recognition, 2014, 47(4): 1721-1730.

[9] 魏巍, 刘勇奎, 段晓东, 等. 三维模型面片链码表示方法[J]. 计算机辅助设计与图形学学报, 2017, 29(3): 537-548. WEI W, LIU Y K, DUAN X D, et al. Representation method of 3D model mesh chain code[J]. Journal of Computer-Aided Design & Computer Graphics, 2017, 29(3): 537-548 (in Chinese).

[10] LORENSEN W E, CLINE H E. Marching cubes: a high resolution 3D surface construction algorithm[C]//Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM Press, 1987: 163-169.

[11] ACHANTA R, SHAJI A, SMITH K, et al. SLIC superpixels compared to state-of-the-art superpixel methods[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(11): 2274-2282.

[12] FABIJANSKA A, GOCLAWSKI J. The segmentation of 3D images using the random walking technique on a randomly created image adjacency graph[J]. IEEE Transactions on Image Processing, 2015, 24(2): 524-537.

[13] TASLI H E, CIGLA C, ALATAN A A. Convexity constrained efficient superpixel and supervoxel extraction[J]. Signal Processing: Image Communication, 2015, 33: 71-85.

[14] 侯增选, 张定华, 杨海成, 等. 体素模型表面优化提取方法及图形显示[J]. 机械科学与技术, 2005, 24(3): 361-363,367. HOU Z X, ZHANG D H, YANG H C, et al. A new optimal method for surface extraction of the voxel model and graphic display[J]. Mechanical Science and Technology, 2005, 24(3): 361-363,367 (in Chinese).

[15] HUTTENLOCHER D P, KLANDERMAN G A, RUCKLIDGE W J. Comparing images using the Hausdorff distance[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1993, 15(9): 850-863.

Compression of directed surface chain code in 3D model

LIU Shang-wu1,2, WEI Wei1,2,3, DUAN Xiao-dong1,2, LIU Yong-kui1

(1. School of Computer Science and Engineering, Dalian Minzu University, Dalian Liaoning 116600, China; 2. Dalian Key Laboratory of Digital Technology for National Culture, Dalian Minzu University, Dalian Liaoning 116600, China; 3. School of Information Science and Technology, Dalian Maritime University, Dalian Liaoning 116026, China)

Firstly, an improved MC normalization method was proposed that was applicable to 3D triangular face chain code algorithm. The per unit length in voxel was set as 2 in the improved MC algorithm, and the 27 points in a voxel was employed to rebuild a contoured surface, eventually obtaining the high-quality standardization triangular mesh model. Secondly, with the new normalization model, a new face traverse method was proposed. Based on the 3D triangular face chain code algorithm, the priority traversal right connection face principle was utilized to take control of the direction of face traverse. This method can reduce the number of traverses, and extend the average length of the face chain code. Experimental results show that the new normalization and the new traversal method, compared with the original 3D triangular face chain code, can significantly improve the compression effect.

face chain code; 3D model; voxel; normalization

TP 391

10.11996/JG.j.2095-302X.2021020237

A

2095-302X(2021)02-0237-08

2020-08-09；

9 August，2020；

2020-08-23

23 August，2020

辽宁省教育厅科研项目(LJYT201911)

Scientific Research Project of Liaoning Education Department (LJYT201911)

刘尚武(1994-)，男，河南南阳人，硕士研究生。主要研究方向为计算机图形学。E-mail：605964270@qq.com

LIU Shang-wu (1994-), male, master student. His main research interest covers computer graphics. E-mail：605964270@qq.com

魏 巍(1980–)，男，河南安阳人，副教授，博士。主要研究方向为计算机图形学。E-mail：weiwei@dlnu.edu.cn

WEI Wei (1980-), male, associate professor, Ph.D. His main research interest covers computer graphics. E-mail：weiwei@dlnu.edu.cn