MomSn(m+n≤8)团簇的结构、稳定性和 电子性质

周岳珍 ，卢 勇 ，刘大春 , ，陈秀敏 , ，李 玮 ，徐俊杰

(1. 昆明理工大学 真空冶金国家工程实验室，昆明 650093； 2. 昆明理工大学 云南省有色金属真空冶金重点实验室，昆明 650093； 3. 昆明理工大学 云南省复杂有色金属资源清洁利用国家重点实验室(培育基地)，昆明 650093)

近年来，随着基本物质结构理论研究的深入，VIB族元素团簇及其掺杂元素引起了人们的关注。钼原子具有特殊的价电子组态(4d55s1)，即d、s 壳层均处于半满填充。因此，对钼及其硫化物的显微结构和形成机理的探索引起了研究人员的广泛关注。目前，有关Mon团簇的研究，已有大量的文献报道。DELLY 等[1]采用自洽场局域自旋密度近似方法计算了Mo2基态结构的键长和离解能；ZHANG 等[2]采用GGA-PW91 方法计算了Mon(n 为2～55)团簇在一维、二维、三维的平衡几何结构；陈杭等[3]采用密度泛函理论下的广义梯度近似(GGA)方法，通过团簇的平衡几何结构、二阶能量差分、垂直电离势、能隙和磁性等性质对过渡金属团簇Mon(n 为2～10)进行系统的探讨；LEI 等[4]采用密度泛函理论下的GGA 方法，研究了Mon(n 为2～8)团簇的平衡几何结构及其对N2分子的吸附行为。

目前，对Mo-S 团簇的研究已有少量报道。WU等[5]研究了MoS6-和MoS6团簇的结构和电子性质；章永凡等[6]研究了Mo2S4团簇的电子结构和光谱性质； MURUGAN 等[7-8]研究了Mo5Sn(n 为5～15)团簇、MonSm(n 为1～6, m 为n～3n)团簇的基态结构及相关性质。然而，上述研究主要集中于某一或某一区间的原子总数范围中的Mo-S 团簇的基态结构及相关性质的计算。本文作者主要计算了包含MomSn团簇随原子总数(m+n)值由2 递增至8 的所有的28 种团簇的基态结构及相关性质。

区别于传统的辉钼矿处理的火法和湿法工艺，辉钼矿真空热分解工艺具备高金属回收率、低生产成本和无环境污染等优势，有着良好的应用前景。二硫化钼作为辉钼矿中钼元素存在的主要形式，其在真空下热分解的反应机理以及钼、硫元素在高温、真空条件下的挥发行为对于辉钼矿真空热分解制备金属钼具有重要意义。因此，以本实验的计算结果为基础，后续将进行高温、真空条件下Mom、Sn和MomSn团簇的从头算分子动力学模拟的计算工作。综合分析模拟计算结果和试验结果，从而为辉钼矿真空热分解制备金属钼的冶金新工艺提供理论指导。

1 计算方法

采用密度泛函的方法对MomSn(m+n≤8)团簇进行结构优化和电子结构计算，全部计算均在量子化学计算程序Materials Studio 6.0 下的Dmol3 软件包中进行。在结构优化过程中，力、位移和能量的收敛标准分别为0.002 Ha/Å、0.005Å 和10-5Ha。在电子结构计算中，采用带极化的双数值原子基组(DNP)，交换关联泛函为GGA[9]，关联梯度修正为PW91 自洽过程以体系的能量是否收敛为依据，自洽场收敛标准为10-6a.u.[10]。为了加速自洽场收敛，使用DIIS 方法，轨道计算中使用的Smearing 标准为0.005 Ha。

为了考察所选择的方法是否合理，计算了Mo2和S2的键长、平均结合能与振动频率，并将计算结果与前人的理论计算值和实验值相比较，如表1 所列。由表1 可知，所选择方法计算的结果基本上与前人的理论计算值相一致，部分数值优于前人的理论计算值，总体上与实验值十分接近。

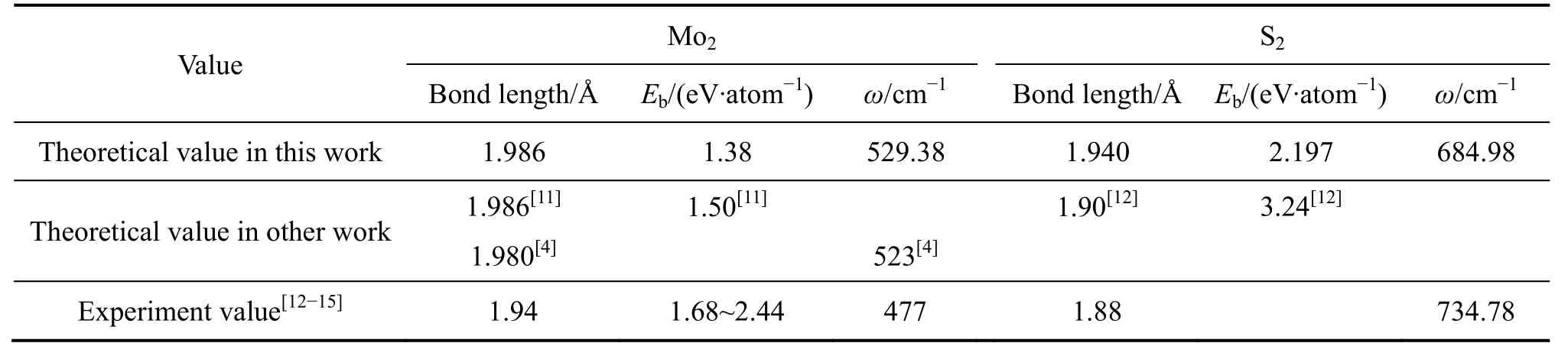
表1 Mo2 和S2 的键长、平均结合能(Eb)和振动频率(ω)的实验值和理论计算值 Table 1 Experimental values and theoretical calculated values of bond length, average binding energy and vibration frequency of Mo2 and S2

在考虑团簇的初始几何构型时，由于随着原子数目的增大，团簇几何构型种类呈现数量级的增大。因此，主要参照了前人研究中涉及到的Sn和Mom团簇的基态几何结构，同时还参照了其他单元素团簇(如Bn、Wn、Ptn、Cdn、Nin、Cun团簇等)的基态几何构 型[16-21]，确定了Mom和Sn团簇的基态几何构型，并选用这些构型作为MomSn团簇合理的起始构型。以上述起始构型为基础，参照GanAs、WnNim团簇等的基态几何构型[22-24]，进行合理的替换、添加等操作，得到MomSn团簇的候选构型。最后，对于每个几何结构，首先允许总磁矩(自旋度)在Dmol3 软件的自动设置下被优化到最优状态(Sz)，接着考虑设置近邻态(Sz±2)或更大范围的自旋态进行再次优化，这两步可以确保所获得的自旋态是团簇的最低能量态[25]。最终，对所有可能的最低能量构型进行能量和频率的计算，把能量最低且振动频率全为正值的构型确定为MomSn团簇的基态几何构型。

2 计算结果与讨论

2.1 团簇的基态几何构型

图1～3 所示分别为Sn团簇、Mom团簇和MomSn团簇的基态几何构型。

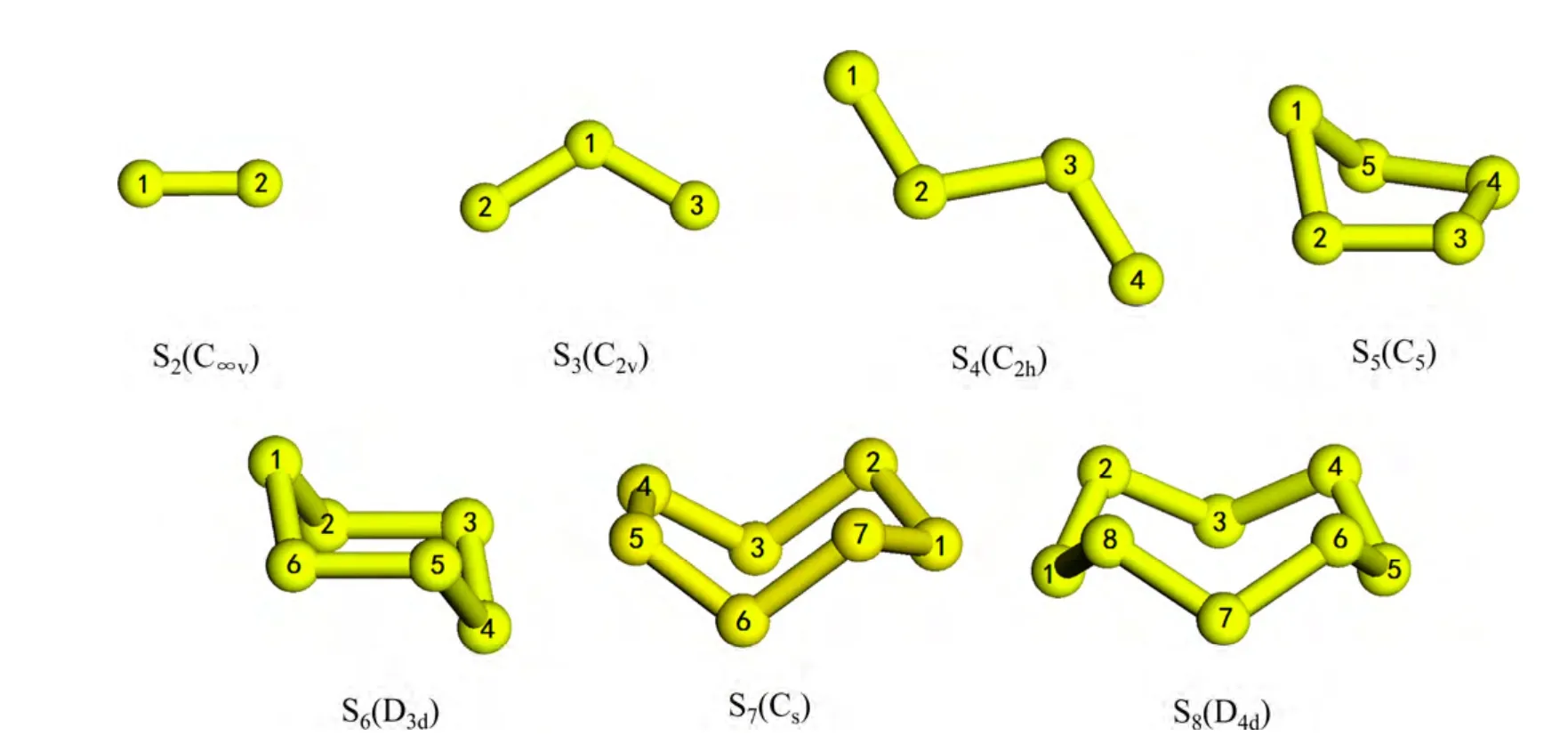
图1 Sn(2≤n≤8)团簇的基态几何构型 Fig. 1 Ground-state geometric structures of Sn(2≤n≤8) clusters

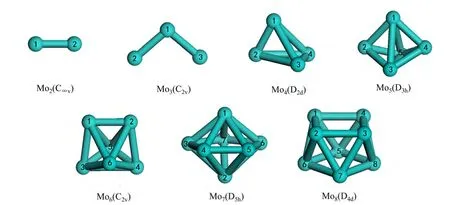
图2 Mom(2≤m≤8)团簇的基态几何构型 Fig. 2 Ground-state geometric structures of Mom(2≤m≤8) clusters

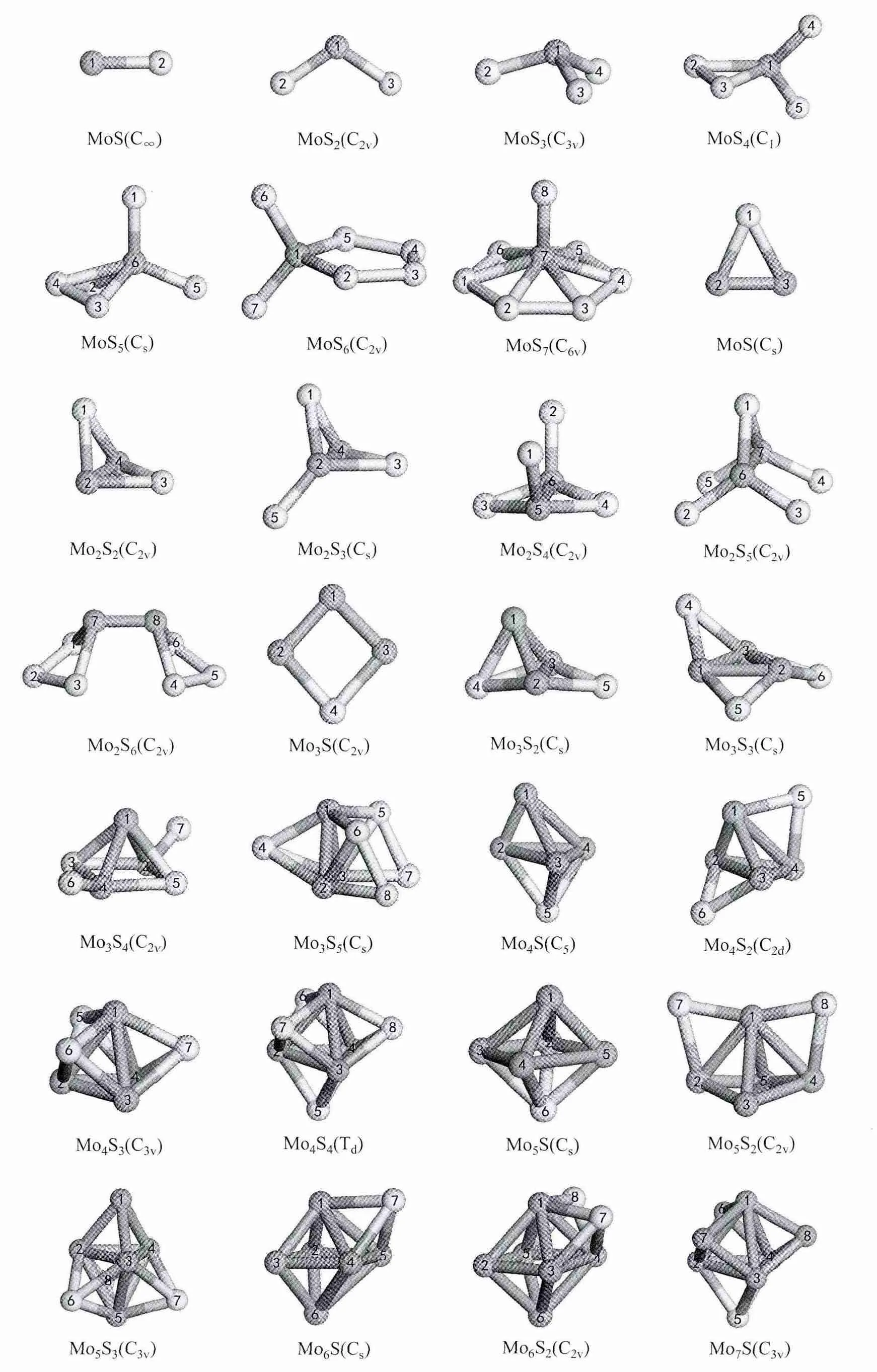
图3 MomSn(m+n≤8)团簇的基态几何构型 Fig. 3 Ground-state geometric structures of MomSn(m+n≤8) clusters

通过对比分析可知，MomSn团簇的基态几何构型与Sn团簇、Mom团簇的基态几何构型密切相关，MomSn团簇的基态几何构型往往以Sn团簇、Mom团簇的基态几何构型作为基础，通过替换或添加若干个原子从而 形成基态几何构型的。如MoS2团簇是以S3团簇为基础，用1 个钼原子替换1 号硫原子形成的；Mo4S 团簇是以Mo4团簇为基础，添加1 个硫原子而形成的。同时，部分MomSn团簇的基态几何构型并不依赖于Sn团簇、Mom团簇的基态几何构型，如Mo2S5团簇。同时，随着团簇尺寸的增大，MomSn团簇的基态结构由较为松散的平面结构向紧凑型的空间结构转变，主要以三角或四角双锥结构为基本单元，通过边戴帽或面戴帽的方式形成稳定的基态结构。

2.2 团簇的稳定性及电子性质

为了确定MomSn团簇的稳定性，计算了不同尺寸MomSn团簇的二阶能量差分 Δ2Em、平均结合能Eb(MomSn)、分裂能D(m)、最高分子占据轨道HOMO、最低分子空轨道LUMO 和能隙HLG，其计算结果如图4～6 所示。

二阶能量差分的定义如式(1)所示：

式中：E(MomSn)为MomSn团簇的总能量。

分裂能的定义如式(2)所示[26]：

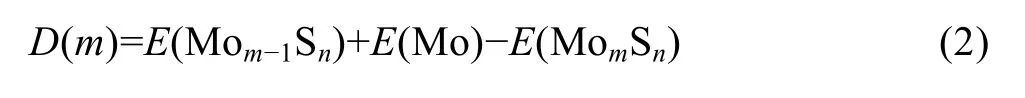
二阶能量差分与分裂能均可用于表征团簇稳定性随尺寸的变化，二阶能量差分与分裂能越大说明其对应的团簇的稳定性越高。

图4 所示为MomSn团簇的二阶能量差分和分裂能随团簇尺寸的变化。由图4 可知，当n=4 时，Mo2Sn团簇的二阶能量差分与分裂能出现峰值，说明Mo2S4团簇比邻近的Mo2S3团簇和Mo2S5团簇更稳定。因此，n=4 应该是Mo2Sn团簇的幻数。然而，对于Mo3Sn团簇的幻数，通过二阶能量差分与分裂能得出的结论是不同的，前者认为n=2，后者认为n=3。因此，n 为2、3 可能是Mo3Sn团簇的幻数，有待进一步对比分析。

平均结合能的定义如式(3)所示：

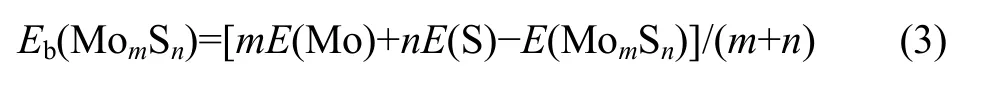
式中：E(Mo)、E(S)分别为自由Mo 原子的能量和自由S 原子的能量，用于表征原子数(m+n)对MomSn团簇几何和能态结构的影响[27]。

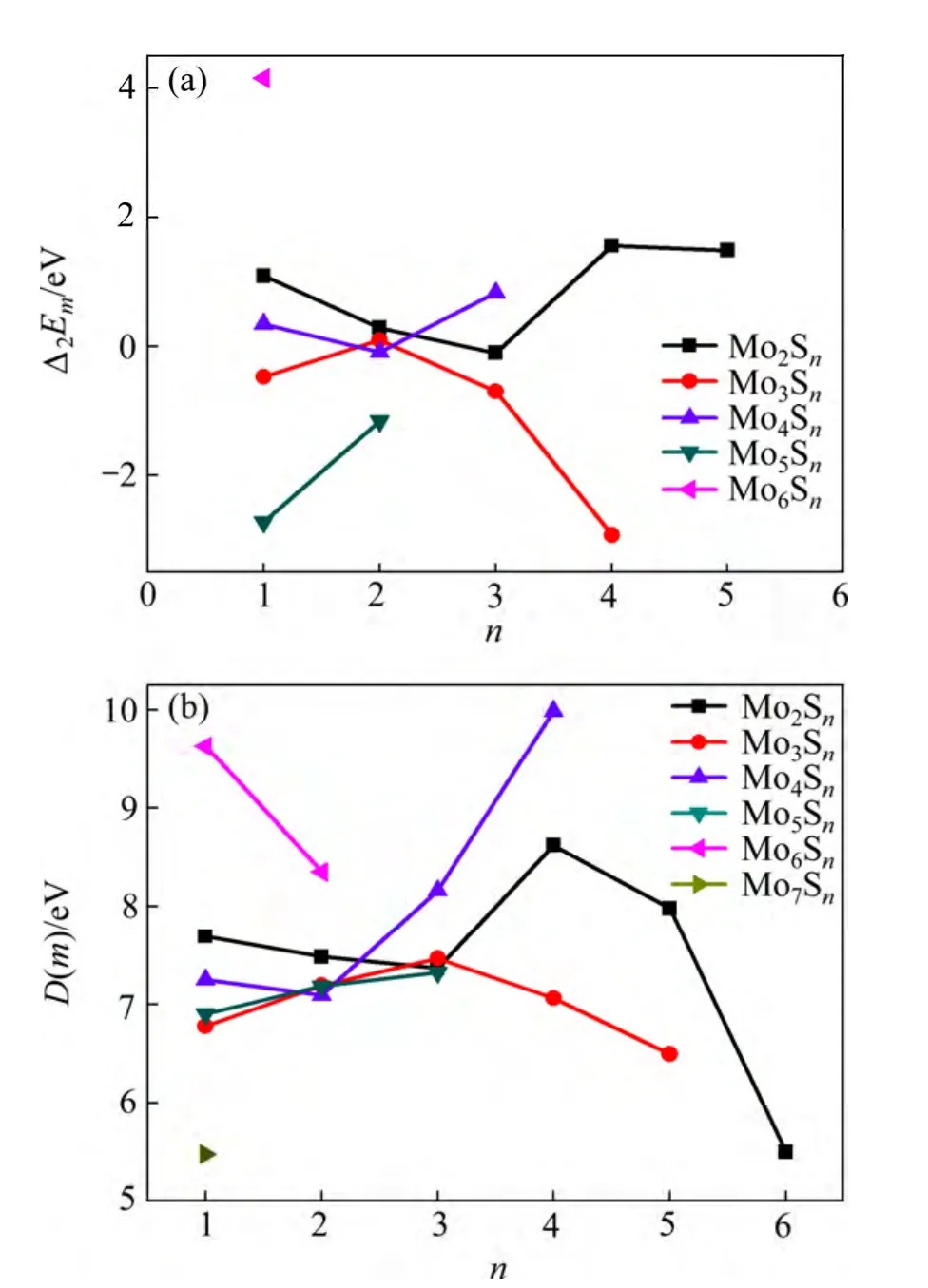
图4 MomSn(m+n≤8)团簇的二阶能量差分Δ2Em 和分裂能D(m) Fig. 4 Second-order difference energy Δ2Em (a) and fission energy D(m) (b) of MomSn(m+n≤8) clusters

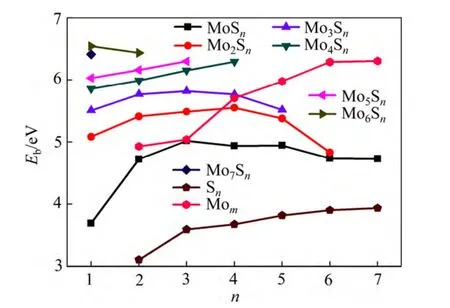
图5 MomSn(m+n≤8)团簇的平均结合能 Fig. 5 Average binding energy of MomSn(m+n≤8) clusters

图5 所示为MomSn团簇的平均结合能随团簇尺寸的变化。由图5 可知，所有MomSn团簇的平均结合能明显高于Sn团簇的平均结合能，绝大多数的MomSn团簇的平均结合能高于Mom团簇的平均结合能，说明 Mo 原子的添加有利于提高主体Sn团簇的稳定性。同理，S 原子的添加有利于提高主体Mom团簇的稳定性。当n=4 时，Mo2Sn团簇的平均结合能出现峰值，说明Mo2S4团簇比邻近的Mo2S3团簇和Mo2S5团簇更稳定，这和分析二阶能量差分、分裂能时所得到的结论是一致的。因此，n=4 是Mo2Sn团簇的幻数。另外，当n为3、5 和n 为2、3 时，MoSn团簇和Mo3Sn团簇的平均结合能出现峰值，但是峰值并不明显，因此无法作为判定MoSn团簇和Mo3Sn团簇幻数结构的依据，有待进一步对比分析。

为了进一步验证MomSn团簇的稳定性及其幻数结构，计算了MomSn团簇的HOMO、LUMO 以及HGL值，图6 所示为其值随MomSn团簇尺寸的变化。

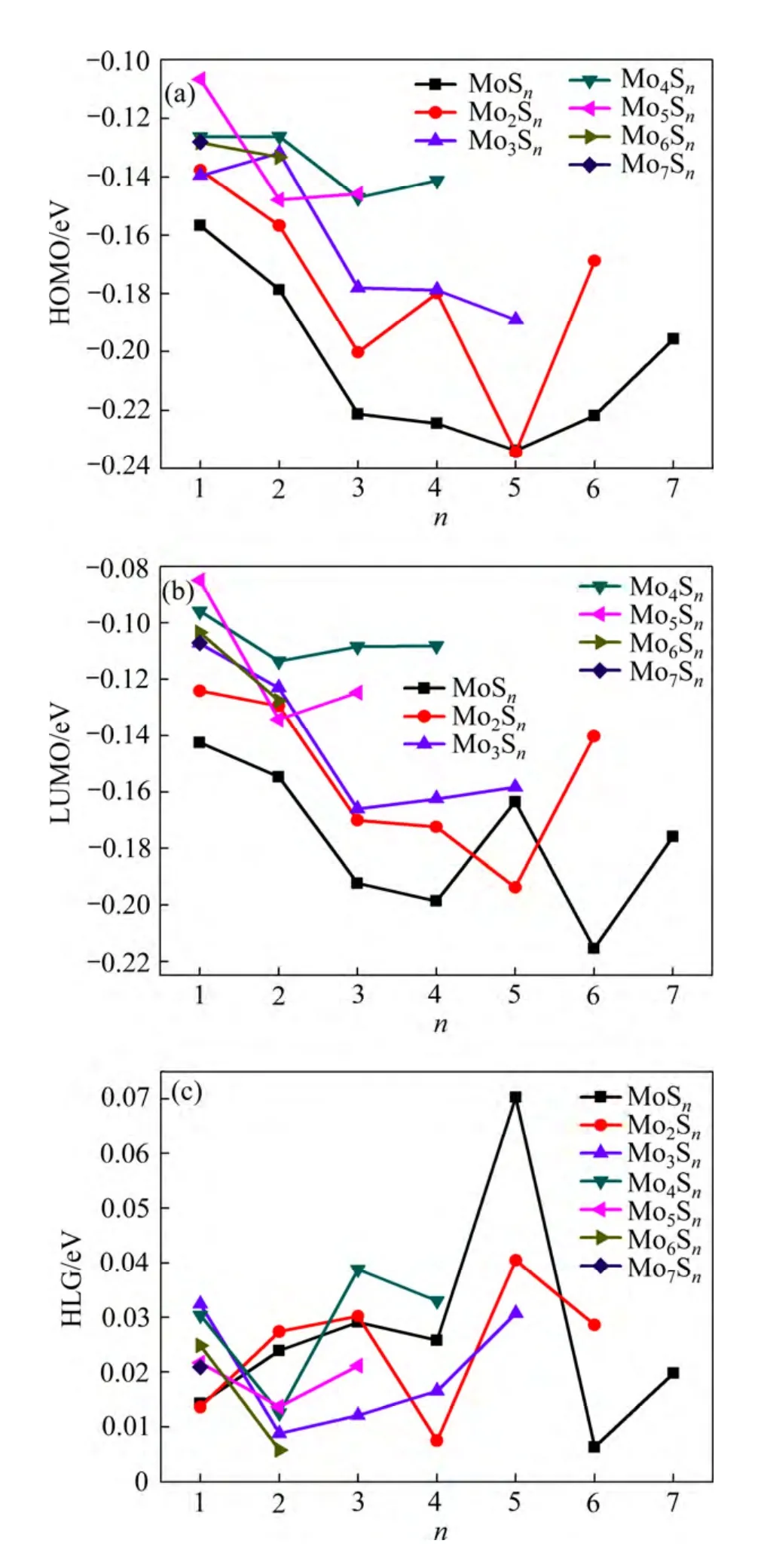
图6 MomSn(m+n≤8)团簇的HOMO、LUMO、HLG Fig. 6 HOMO(a), LUMO(b), HLG(c) of MomSn(m+n≤8) clusters

最高分子占据轨道(HOMO)的负值近似等于该物质的第一电离能，其值越大，对应的团簇分子越易失 去电子。最低分子空轨道(LUMO)的能级数值上与该物质的电子亲和势相当，其值越小，该分子越易得到电子。HOMO 和LUMO 的能隙(HLG)反映了电子从HOMO 能级跃迁到LUMO 能级的能力，在一定程度上代表了该分子参与化学反应的能力[28]，其值越大，团簇分子的化学活泼性越低，对应的团簇化学稳定性就越强。由图6 可知，当n 为5 和3 时，MoSn团簇和Mo4Sn团簇能隙的对应位置分别出现峰值，且峰值明显。即较MoSn团簇和Mo4Sn团簇中的其他团簇而言，MoS5团簇和Mo4S3团簇得失电子相对困难，化学性质更为稳定一些。

总之，通过分析不同尺寸MomSn团簇的二阶能量差分Δ2Em、平均结合能Eb(MomSn)、分裂能D(m)、最高占据轨道HOMO、最低空轨道LUMO 和能隙HLG，可得如下结论：MoSn团簇、Mo2Sn团簇、Mo3Sn团簇的幻数分别为5、4、3。

2.3 团簇的Mulliken 布局分析

为了分析MomSn团簇中的键合性质，即离子键与共价键的成分，对MomSn团簇中的S 原子和Mo 原子进行Mulliken 布局分析。由于在MomSn团簇中电荷的转移主要发生在S 和与S 成键的Mo 之间，少量地发生在Mo 与Mo 之间。因此，仅对MomSn团簇中的S和与S 成键的Mo 进行Mulliken 布局分析，表2 所列为计算结果。

由表2 可知，所有的S 原子均带负电，电荷为-0.069～-0.587 e；所有的Mo 原子均带正电，电荷为0.004～0.867 e，说明在MomSn团簇中电荷均由Mo 原子向S 原子转移，符合Mo、S 电负性的一般规律，Mo—S 键具有离子键的特性。

3 结论

1) MomSn团簇的基态几何构型与Sn团簇、Mom团簇的基态几何构型密切相关，前者往往以后者作为基础，通过替换或添加若干个原子从而形成基态几何构型的。

2) Mo 原子的添加有利于提高主体Sn团簇的稳定性；S 原子的添加有利于提高主体Mom团簇的稳定性。

3) 通过二阶能量差分、平均结合能、分裂能、最高分子占据轨道和最低分子空轨道间的能隙等的详细 分析，MoSn团簇、Mo2Sn团簇、Mo3Sn团簇的幻数(n)分别为5、4、3。

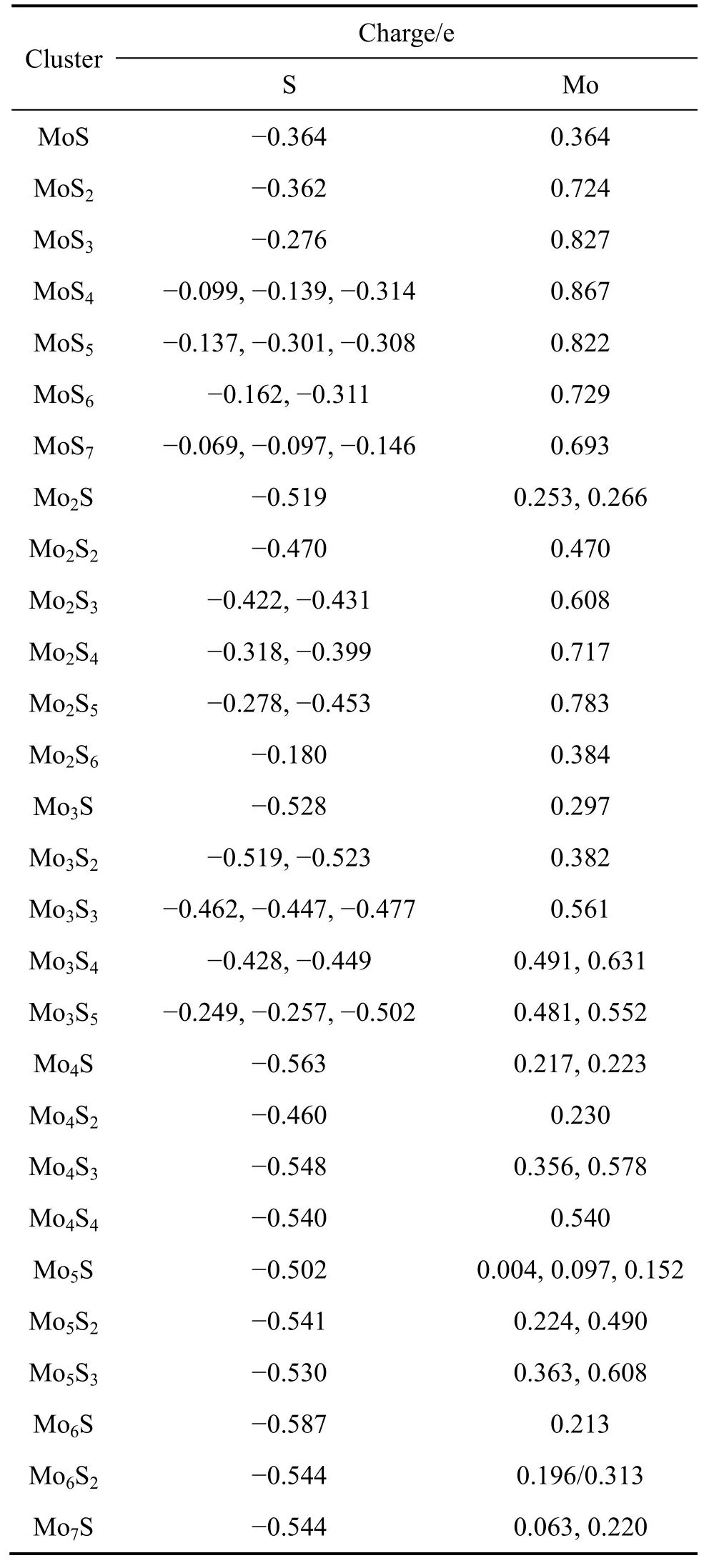
表2 S 和与S 成键的Mo 的布局分析 Table 2 Mulliken population analysis for S and Mo binding with S

4) 在MomSn团簇中，电荷均是由Mo 原子向S 原子转移的，表明Mo—S 键具有离子键的特性。

5) 计算得到的MomSn(m+n≤8)团簇的最低能量结构，将作为后续计算中的高温、真空条件下MomSn团簇动力学模拟的重要参考依据，从而为硫化钼的真空热分解实验的组分挥发问题提供理论解释。

[1] DELLEY B, FREEMAN A J, ELLIS D E. Metal-metal bonding in Cr-Cr and Mo-Mo dimers: Another success of local spin-density theory[J]. Physical Review Letters, 1983, 50(7): 488-491.

[2] ZHANG Wen-qin, RAN Xiao-rong, ZHAO Hai-tao, WANG Li-chang. The nonmetallicity of molybdenum clusters[J]. The Journal of Chemical Physics, 2004, 121(16): 7717-7724.

[3] 陈 杭, 雷雪玲, 刘立仁, 祝恒江. Mon(n=2～10)团簇结构和性质的密度泛函理论研究[J]. 原子与分子物理学报, 2009, 26(6): 1048-1056. CHEN Hang, LEI Xue-Lin, LIU Li-reng, ZHU Heng-jiang. Density functional theory study of the structures and electronic properties of Mon(n=2-10) clusters[J]. Journal of Atomic and Molecular Sciences, 2009, 26(6): 1048-1056.

[4] LEI Xue-ling. Theoretical study of small Mo clusters and molecular nitrogen adsorption on Mo clusters[J]. Chinese Physics B, 2010, 19(10): 107103.

[5] WU Ni, ZHANG Chang-fu, ZHOU Qi, HUANG Xin, ZHANG Yong-fan, Ding Kai-ning, WANG Bin. DFT study on the electronic and structural properties of MoS6-/0clusters[J]. Chinese Journal of Structural Chemistry, 2013, 32(7): 1046-1054.

[6] 章永凡, 吴立明, 李 俊, 黄尊行, 胡建明, 周立新. 簇合物Mo2X4(X=S,O)电子结构和光谱性质的Ab Initio 研究[J]. 高等学校化学学报, 1998, 19(10): 1659-1665. ZHANG Yong-fan, WU Li-ming, LI Jun, HUANG Zun-xing, HU Jian-ming, ZHOU Li-xin. Ab initio study on the electronic structures and the spectra properties of the Mo2X4(X=S,O) clusters[J]. Chemical Journal of Chinese Universities, 1998, 19(10): 1659-1665.

[7] MURUGAN P, KUMAR V, KAWAZOE Y, OTA N. Understanding the structural stability of compound Mo-S clusters at sub-nanometer level[J]. Materials Transactions, 2007, 48(4): 658-661.

[8] MURUGAN P, KUMAR V, KAWAZOE Y, OTA N. Ab initio study of structural stability of Mo-S clusters and size specific stoichiometries of magic clusters[J]. The Journal of Physical Chemistry A, 2007, 111(14): 2778-2782.

[9] PERDEW J P, WANG Y. Accurate and simple analytic representation of the electron-gas correlation energy[J]. Physical Review B, 1992, 45(33): 13244-13249.

[10] DELLY B. An all-electron numerical method for solving the local density functional for polyatomic molecules[J]. The Journal of Chemical Physics, 2000, 92(1): 508-517.

[11] 陈 杭. 钼团簇及氮化钼团簇几何结构和电子性质的密度泛函理论研究[D]. 乌鲁木齐: 新疆师范大学, 2010: 25-26. CHEN Hang. Density functional theory studies on the structures and electronic properties of Mo and Mo2N clusters[D]. Wulumuqi: Xinjiang Normal University, 2010: 25-26.

[12] BAI Yu-lin, CHENG Xiang-rong, YANG Xiang-dong, LU Peng-fei. Structures of small sulfur clusters Sn(n=2-8) from Langevin molecular dynamics methods[J]. Acta Physico- Chimica Sinica, 2003, 19(12): 1102-1107.

[13] EFREMOV Y M, SAMOILOVA A N, KOZHUKHOVSHY V B. On the electronic spectrum of the Mo2molecule observed after flash potolysis of Mo(CO)6[J]. Journal of Molecular Spectroscopy, 1978, 73(3): 430-440.

[14] HOPKINS J B, LANGRIDGE-SMITH P R R, MORSE M D, SMALLEY R E. Supersonic metal cluster beams of refractory metals: spectral investigations of ultracold Mo2[J]. The Journal of Chemical Physics, 1983, 78(4): 1627-1637.

[15] 李俊玉. 硫微团簇分子离子的结构与解析势能函数研究[D]. 新乡: 河南师范大学, 2005: 26-27. LI Jun-yu. Ab initio calculation of molecular and ionic structures and potential energy function of small sulfur clusters[D]. Xinxiang: Henan Normal University, 2005: 26-27.

[16] 王剑锋. 过渡金属Sc, Ti 掺杂硼团簇结构与稳定性的密度泛函理论研究[D]. 临汾: 山西师范大学, 2012: 20-24. WANG Jian-feng. Structure and stability of TiBn, ScBnand TimBnclusters[D]. Linfen: Shanxi Normal University, 2012: 20-24.

[17] 张秀荣, 康张李, 李 扬. WnC0,±(n=1, …, 6) 团簇结构与电子性质的理论研究[J]. 计算物理, 2011, 28(4): 598-604. ZHANG Xiu-rong, KANG Zhang-li, LI Yang. Structure and electronic properties of WnC0,±(n=1, …, 6) clusters[J]. Chinese Journal of Computational Physics, 2011, 28(4): 598-604.

[18] 吴 珊, 王怀谦, 李嘉琪, 李颖钰, 余逸男, 韩 佳. 铂金团簇结构与稳定性的密度泛函研究[J]. 华侨大学学报(自然科学版), 2015, 36(1): 35-39. WU Shan, WANG Huai-qian, LI Jia-qi, LI Ying-yu, YU Yi-nan, HAN Jia. Density functional theory study of the structures and relative stabilities of platinum clusters[J]. Journal of Huaqiao University (Natural Science), 2015, 36(1): 35-39.

[19] 智丽丽, 李艳青, 古丽娜, 张保花, 赵高峰. Cd 团簇的第一性原理研究[J]. 原子与分子物理学报, 2012, 29(1): 76-80. ZHI Li-li, LI Yan-qing, GU Li-na, ZHANG Bao-hua, ZHAO Gao-feng. Density functional study of the Cd clusters[J]. Journal of Atomic and Molecular Sciences, 2012, 29(1): 76-80.

[20] YAN Shi-ying, JIANG Hai. Structure of small Nin(n≤8) clusters[J]. Chinese Journal of Computational Physics, 2012, 29(4): 611-619.

[21] 杨宗献, 谢罗刚. Cux(x=1～4)团簇在CeO2(111)表面的吸附[J]. 物理化学学报, 2011, 27(4): 851-857. YANG Zong-xian, XIE Luo-gang. Adhesion of small Cux(x=1-4) clusters on a CeO2(111) surface[J]. Acta Physico-Chimica Sinica, 2011, 27(4): 851-857.

[22] 马德明, 乔红波, 李恩玲, 施 卫, 马优恒. 富镓 GanAs (n=1～9)团簇稳定性及缺陷特性的密度泛函理论研究[J]. 原子与分子物理学报, 2014, 31(2): 223-228. MA De-ming, QIAO Hong-bo, LI En-ling, SHI Wei, MA You-heng. Density functional theory study on stability and defect feature of Ga-rich GanAs(n=1-9) clusters[J]. Journal of Atomic and Molecular Sciences, 2014, 31(2): 223-228.

[23] 张秀荣, 李 扬, 杨 星. WnNim(n+m=8)团簇结构与电子性质的理论研究[J]. 物理学报, 2011, 60(10): 236-245. ZHANG Xiu-rong, LI Yang, YANG Xing. Theoretical study on structural and electronic properties of WnNim(n+m=8) clusters[J]. Chinese Journal of Physics, 2011, 60(10): 236-245.

[24] 董 闯, 羌建兵, 袁 亮, 王 清, 王英敏. 合金相的“团簇+连接原子”模型与成分设计[J]. 中国有色金属学报, 2011, 21(10): 2502-2510. DONG Chuang, QIANG Jian-bing, YUAN Liang, WANG Qing, WANG Ying-min. A cluster-plus-glue-atom model for composition design of complex alloys[J]. The Chinese Journal of Nonferrous Metals, 2011, 21(10): 2502-2510.

[25] 秦健萍, 梁瑞瑞, 吕 瑾, 武海顺. ComAln(m+n≤6)团簇的结构和磁性理论研究[J]. 物理学报, 2014, 63(13): 133102. QING Jian-ping, LIANG Rui-rui, LÜ Jin, WU Hai-shun. Structural, electronic and magnetic properties of ComAln(m+n≤6) clusters[J]. Chinese Journal of Physics, 2014, 63(13): 133102.

[26] 阮 文, 谢安东, 余晓光, 伍冬兰. NaBn(n=1～9)团簇的几何结构和电子性质[J]. 物理学报, 2012, 61(4): 043102. RUAN Wen, XIE An-dong, YU Xiao-guang, WU Dong-lan. Geometric structure and electronic characteristics of NaBn(n=1-9) clusters[J]. Chinese Journal of Physics, 2012, 61(4): 043102.

[27] ZHANG Xiu-rong, ZHANG Fu-xing, CHEN Chen, YUAN Ai-hua. Structure and magnetic properties of Osn(n=11-22) clusters[J]. Chinese Physics B, 2013, 22(12): 123102.

[28] 侯 茹, 郭 平, 陈永庄, 张继良, 李书婷, 任兆玉. Nb2Sin-(n=1～6)团簇的几何构型、电子性质和磁性的理论研究[J]. 原子与分子物理学报, 2014, 31(3): 385-392. HOU Ru, GUO Ping, CHEN Yong-zhuang, ZHANG Ji-liang, LI Shu-ting, REN Zhao-yu. A density functional of investigation of Nb2Sin-(n=1-6) clusters[J]. Journal of Atomic and Molecular Sciences, 2014, 31(3): 385-392.