ZX115 镁合金热压缩过程的 本构分析及有限元模拟

丁汉林，徐成志，张晓军 ，潘晓东，王天一

(1. 安徽工业大学 材料科学与工程学院，马鞍山 243002； 2. 中国人民解放军海军工程大学 化学与材料系，武汉 430033； 3. 马鞍山钢铁股份有限公司 第四钢轧总厂，马鞍山 243000)

镁及其合金具有优异的综合性能，如低密度、高比强度和刚度、阻尼减震等，已成为最具潜力的工程结构材料之一，且其综合性能亦可通过合金化和晶粒细化的方式进一步得到优化和改善[1]。目前，镁合金中最常见的添加元素是Zn 和Al 两种元素。研究指 出[2-3]，在Mg-Zn 合金中少量添加Ca 元素可起到细化晶粒和固溶强化的作用，亦可有效提高合金的耐蚀性能。目前，Mg-Zn-Ca 合金的成形方式以铸造为主，并在医用生物材料中逐步得到应用[4-5]。

通过挤压、轧制等热变形后，Ca 元素在镁合金中对弱化形变织构、提高硬度和屈服强度所产生的影响与稀土元素相类似[6-7]，这与其塑性变形行为密切相关，但具体的作用机理并不十分清楚。本文作者已对Mg-Zn-Ca 合金变形过程中的组织演变、动态再结晶机制、织构特征等方面进行了研究和分析[8-9]，但关于Mg-Zn 合金中添加Ca 后的本构方程的研究却鲜见报道。而基于对合金热变形过程中流动应力-应变曲线的分析，探明合金的塑性变形行为及形变参数与动态再结晶之间的相互关系，进而为深入理论分析和数值模拟提供必要的实验数据，也已逐渐成为研究合金塑性变形的另一种有效手段。

王忠堂等[10]在温度为250～350 ℃、应变速率为0.01～1 s-1、最大变形程度为50%条件下对AZ31 镁合金进行热模拟实验研究，并建立该合金高温变形本构关系模型，该本构关系模型的相对计算误差小于13%。CERRI 等[11]用热压缩试验，在应变速率为1.6×10-5～ 10-1s-1、变形温度为125～300 ℃条件下，对高压压铸AZ91 镁合金的热变形行为进行了研究，并计算了其本构方程中的相关常数。本文作者主要根据Mg-1.3Zn-1.7Ca 合金(质量分数，%)(ZX115)Gleeble 单轴热压缩实验所获得的应力-应变曲线，讨论变形条件与峰值应力、峰值应变、动态再结晶之间的关系，尝试建立适用于该合金高温塑性变形的本构方程。将该本构方程应用于有限元分析软件 DEFORM 3D 并对合金的热压缩过程进行数值模拟，利用后处理程序，研究工件内部的应变速率场、应变场和温度场变化等，以期为成型工艺的优化提供依据。

1 实验

实验合金为ZX115 镁合金，其熔炼与铸造工艺、实测成分及热处理条件参见文献[8]。单轴热压缩实验所需试样取自于均匀化处理后的镁合金铸锭，经线切割和机加工的方式制备成尺寸为d 10 mm×15 mm 的轴对称圆柱体。压缩实验在Gleeble-3500 型热模拟试验机上进行，压缩过程中计算机动态记录流变应力与应变量。压缩前，试样两端涂抹石墨润滑，以尽量减少试样与压缩砧头之间的摩擦。变形温度分别设为300、350、400 和450 ℃，应变速率分别设为0.001、0.01、0.1 和1.0 s-1。将圆柱试样装夹在设备中，以 5 ℃/s 速度升温到设定温度，保温60 s 后按照设定的应变速率进行压缩，在各试验条件下试样均压缩至真应变0.7 后卸载。

2 结果与分析

2.1 合金的真应力-应变曲线

图1 所示为不同应变速率下ZX115 合金高温压缩变形的真应力-应变曲线。由图1 中曲线变化趋势可以看出，ZX115 镁合金的流变应力随着应变量的增加而快速上升，达到一定的应变量时，流变应力出现一个峰值，随后随着应变量的继续增加流变应力逐渐降低，当应变量超过0.6 时流变应力下降至某一稳定值并基本保持恒定。由图1 还可看出：当应变速率一定时，ZX115 合金的流变曲线达到的峰值应力和稳态应力随着变形温度的升高而降低；当变形温度一定时，其峰值应力和稳态应力则随着应变速率的升高而升高；在较低应变速率或/和较高变形温度的条件下，流变应力-应变曲线的峰值不太明显，应力呈稳态变化。

结合组织分析[8]可以确定，这一现象主要是由于ZX115 合金热压缩过程中动态再结晶的软化作用与加工硬化作用相互竞争并达到相对平衡的结果所决定的。压缩变形的初始阶段，试样的变形量较小，可开动位错较少，且位错滑移受阻，尤其是对于密排六方结构的镁合金，其位错密度增加相当迅速，应力值随着变形量的增加而快速增大，即发生明显的加工硬化现象。当变形量达到某一临界值时，材料内发生动态再结晶，由于再结晶晶粒的不断形核与长大，由动态再结晶所引起的软化作用逐渐起到决定性作用。另一方面，随着变形量的增大，位错滑移驱动力逐渐增加，从而导致可动位错数量增加，进而使软化作用增强，因此，应力值随着变形量的增加开始缓慢降低，当加工硬化过程与动态再结晶的软化过程达到动态平衡时，应力值降低至某一稳态值。

2.2 本构方程的建立

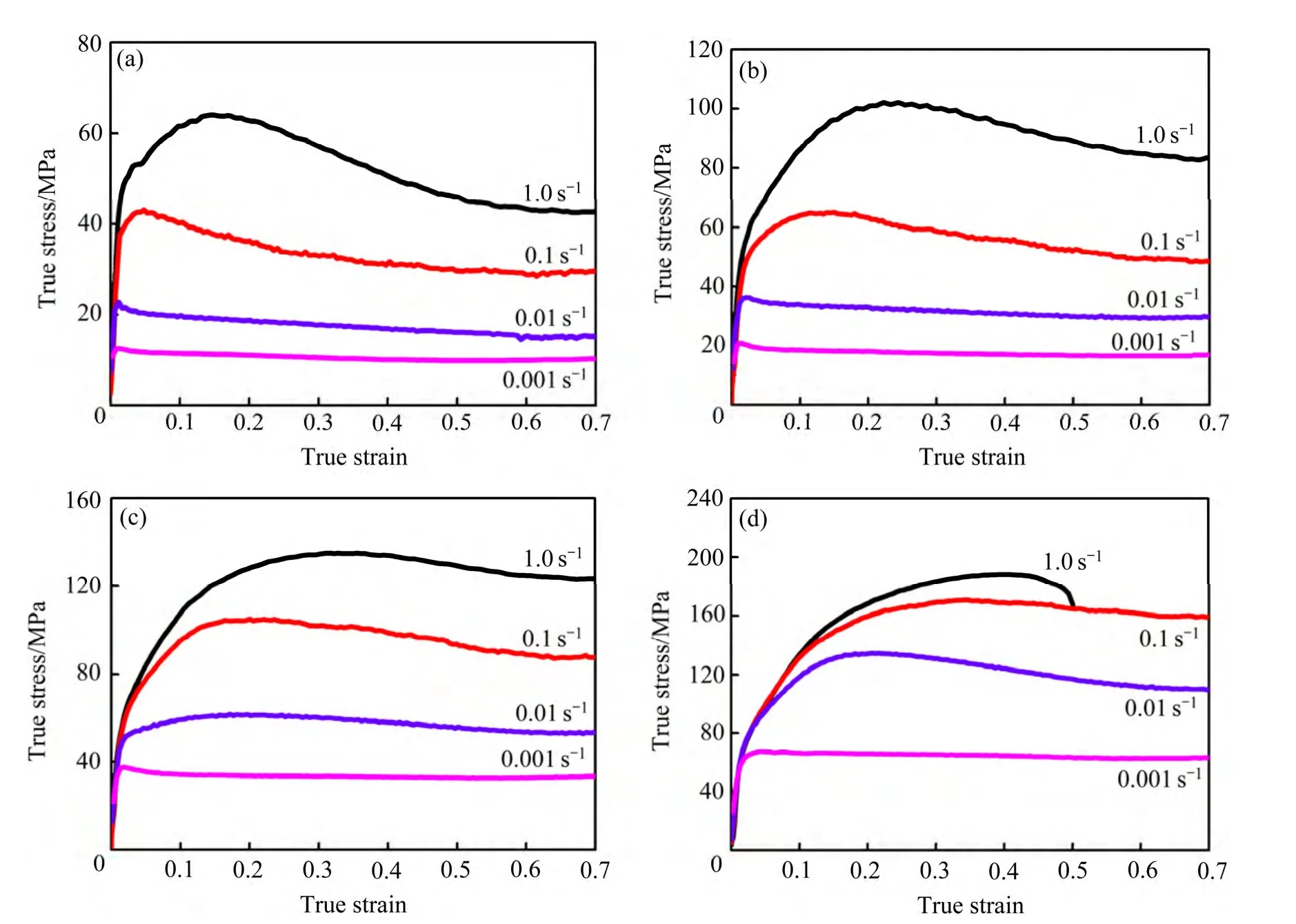
图1 不同变形条件下压缩时ZX115 镁合金的真应力-应变曲线 Fig. 1 True stress-strain curves of ZX115 magnesium alloy obtained from hot compressions under different conditions: (a) 450 ℃; (b) 400 ℃; (c) 350 ℃; (d) 300 ℃

由图1 可以明显看出，ZX115 合金热压缩时的流变应力σ 与应变速率ε˙、温度T 之间存在着密切关系。 因此，有必要研究各个因素之间的相互关系，即通过建立描述其塑性变形过程应力-应变曲线的本构方程来进一步考察合金的高温变形行为[12-13]。SELLARS等[14]提出采用双曲线正弦形式修正的Arrhenius 公式来描述高温变形时这三者之间的关系：

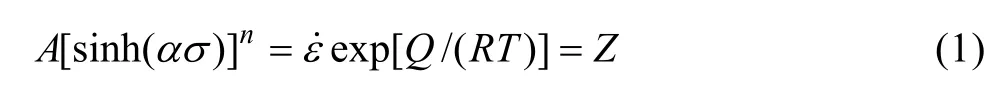
一般来说，在低应力水平情况下，式(1)更接近于指数关系：

而在高应力水平情况下，式(1)更接近于幂指数 关系：

式中：A1、A2、A、n1、n、α 和β 均为与温度无关的常数；R 为摩尔气体常数；T 为绝对温度；Q 为变形激活能；ε˙为应变速率；σ 表示流变应力。一般而言，α 、β 及n1之间满足关系式α =β/n1。

MCQUEEN 等[15]指出，在高温变形的本构方程的研究中，对于镁合金这类易发生动态再结晶的材料而言，常选用峰值应力值(σp)进行计算和分析。表1 所列为在不同变形条件下ZX115 合金真应力-应变曲线上的峰值应力。

分别根据式(2)和(3)分析不同变形条件下热压缩时峰值应力与应变速率之间的关系曲线，结果如图2所示。对图2 中数据进行线性回归可以得出，指数n1=1/0.2014=4.97(见 图 2(a))和 系 数 β=1/12.8302= 0.07794(见 图 2(b))，进 而 可 求 得 参 数 α=β/n1= 0.016 MPa-1。

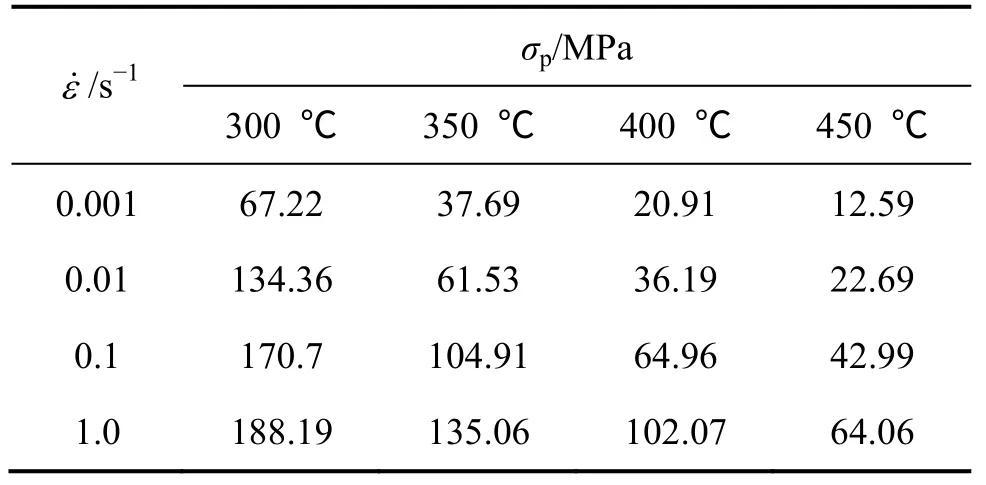
表1 不同变形条件下ZX115 镁合金的峰值应力 Table 1 Peak stress of ZX115 magnesium alloy under different deformation conditions

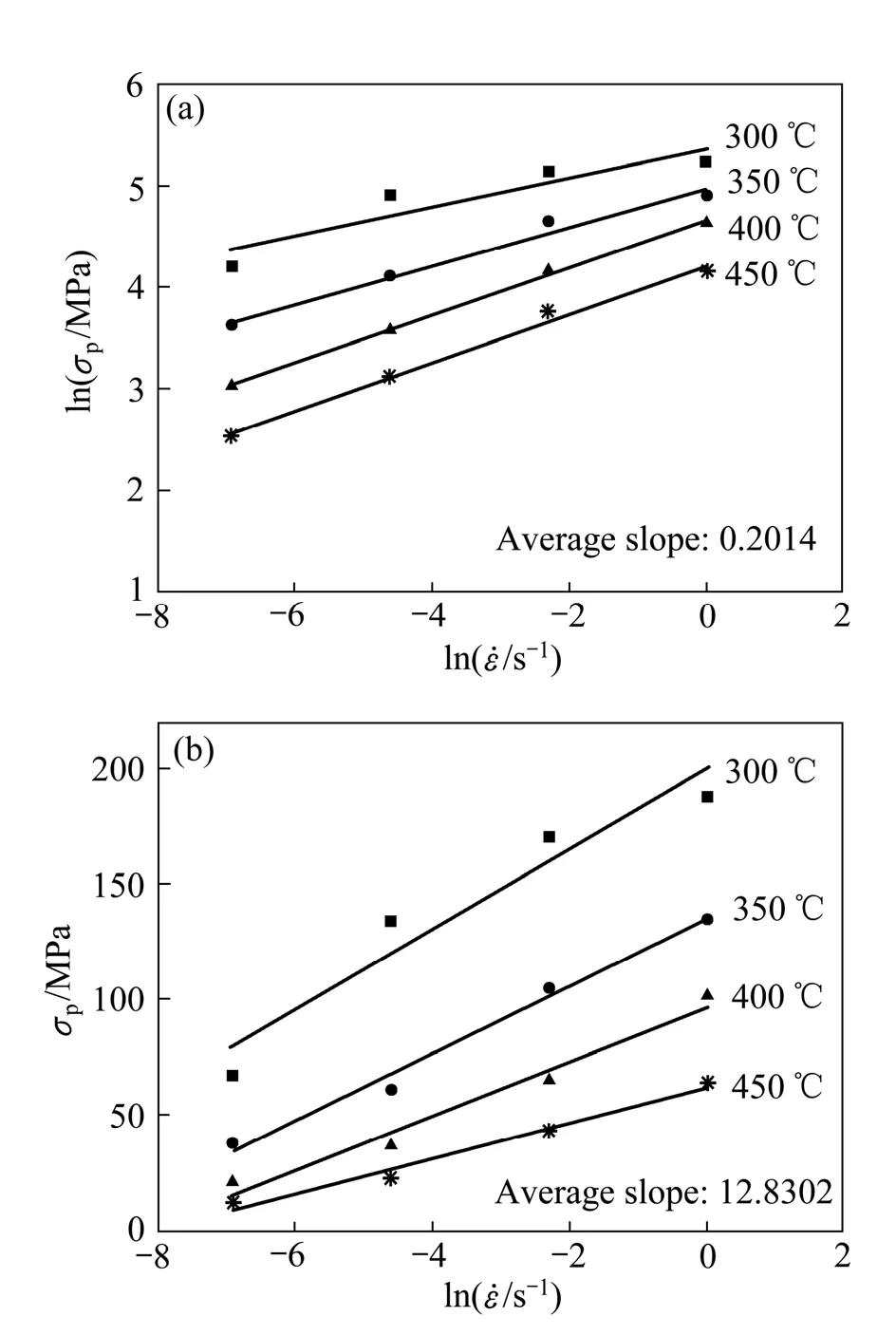
图2 ZX115 镁合金峰值应力与应变速率之间的关系 Fig. 2 Relationship between peak stress and strain rate for ZX115 magnesium alloy according to Eqns. (2) and (3): (a) Exponential relationship according to Eqn. (2); (b) Power- exponential relationship according to Eqn. (3)

对式(1)两边取自然对数可得： lnε˙ = lnA+ [-QRT)]+n ln[sinh(ασ)]。 可 以 看 出， ln ε˙与nln[sinh(ασ)]成线性关系，其斜率即为应力指数n。图3 所示为应变速率与峰值应力之间的双曲正弦关系，其中，α 值取本实验中所得的0.016 MPa-1。由拟合结果可以看出，两者之间较好地符合线性关系，拟合所得不同温度下应力指数的平均值n=3.50。

此外，根据Zener-Hollomon 参数的定义，当应变速率保持不变时，假定在很小的温度变化范围内变形激活能保持不变， 对式(1) 取对数可得lnA+[-Q/(RT)]+nln[sinh(α σ)]= ln+Q/(RT)，由此可得峰值应力与温度之间的关系：ln[sinh(ασ)]=其中，。根据实验数据绘制的ln[sinh(ασ )]- T-1之间的关系曲线如图4 所示。经数据拟合可得，B'=Q/(1000nR)=5.935，其中，n 为材料常数，将以上求得的数据代入，可得ZX115 镁合金的变形激活能Q=172712.9 J/mol≈173 kJ/mol。

图3 ZX115 镁合金应变速率与峰值应力之间的关系曲线 Fig. 3 Relationship between strain rate and peak stress of ZX115 magnesium alloy

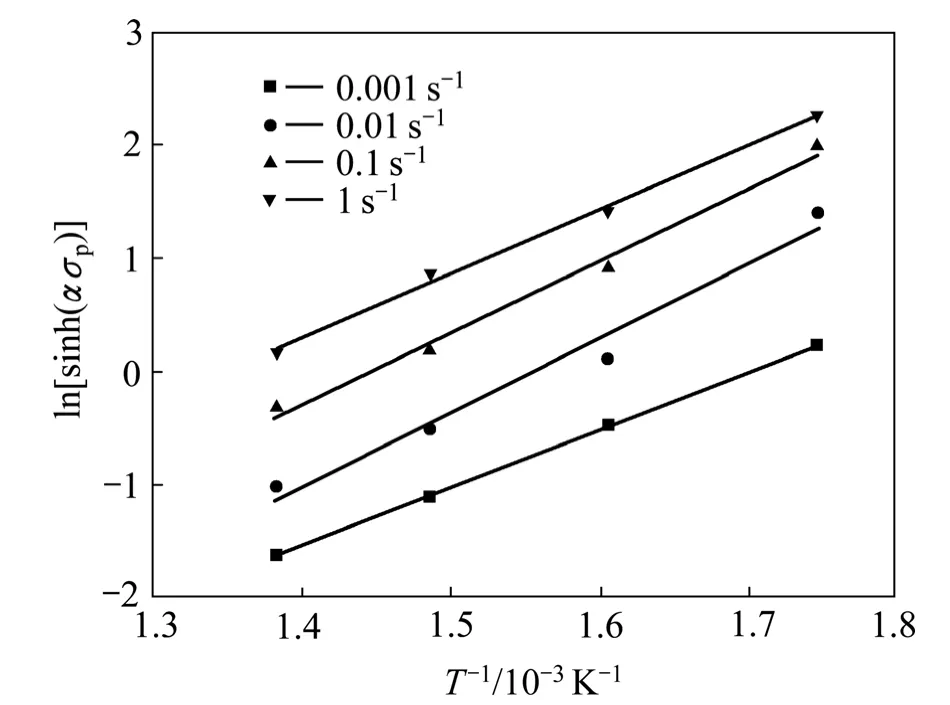
图4 ZX115 镁合金的峰值应力与变形温度之间的关系 Fig. 4 Relationship between peak stress and deformation temperature of ZX115 magnesium alloy

对式(1) 进行对数变换可得： ln Z=ln A+ nln[sinh(ασ)]，其中Z 参数(=exp[Q/(RT)])可用于计算和讨论不同变形条件(不同温度、不同应变速率)与峰值应力之间的关系，其结果如图5 所示。对图5 中的数据进行线性拟合，并设定应力指数n=3.50，可得方程 ln Z=28.6302+3.50 ln[sinh(ασ)]。由此可得： ln A=28.6302，即A=2.716×1012。

综上分析，式(1)中所有材料常数均由实验数据拟合得出，因此，用于描述ZX115 镁合金热压缩变形过程中应力-应变曲线变化的本构方程可表示为

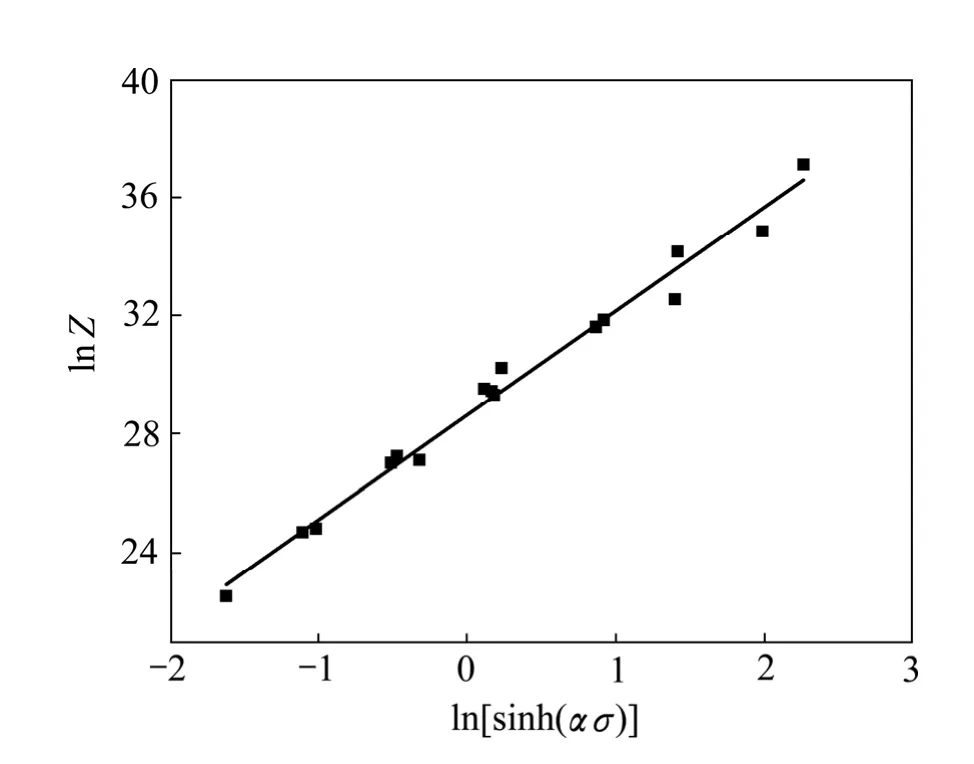
图5 ZX115 镁合金的Z 参数与流动应力之间的关系 Fig. 5 Relationship between Z parameter and flow stress of ZX115 magnesium alloy

就式(1)类型的本构方程而言，在描述铝合金塑性变形的本构方程中α 值通常选取为0.052 MPa-l[15]；RAVI-KUMAR 等[16]和ZHOU 等[17]分别在AZ31 和AZ91 镁合金的本构分析中沿用了这一取值。可能是 由于合金的初始状态(如合金成分、热处理状态、晶粒大小等)和变形工艺(加载方式、变形温度等)不同，SPIGARELLI 等[18]分析AZ31 合金在200～400 ℃之间的变形时得出α 值为0.02 MPa-1；ZHOU 等[19]在分析AZ61 合金均匀化处理后的塑性变形时计算的α 值亦为0.02 MPa-1，而LIU 等[20]通过AZ91 合金的热压缩实验分析其α 值为0.013 MPa-1。在本实验中，ZX115镁合金热压缩变形本构方程中α 值的大小为0.016 MPa-l，这一数值与上述诸多文献中的α 值十分接近。可以推断，对于镁合金而言，无论其合金成分和变形方式是否相同，其本构方程中的α 值均较为接近，因此，可取近似值用于其他镁合金塑性变形的本构分析。

据文献报道，AZ31、AZ61 和AZ91 镁合金的变形激活能分别约为140 kJ/mol[21]、160 kJ/mol[19]和 176 kJ/mol[20]。可见，Mg-Al-Zn 系镁合金的变形激活能随着合金中Al 含量的增加而增加。这是由于随着 Al 含量的增加，Mg-Al-Zn 系镁合金在变形过程中可以析出较多的第二相粒子，而这些弥散分布的粒子在合金的塑性变形过程中会阻碍位错的运动，使位错发生交滑移和攀移所需的能量升高，由此提高合金的变形激活能。在本实验中，经计算得到ZX115 镁合金热压缩过程中的变形激活能为173 kJ/mol，大于镁的自扩散激活能135 kJ/mol 及铝在镁中的扩散激活能 143 kJ/mol[22]，这意味着ZX115 镁合金的塑性变形主要是由位错攀移而不是扩散所控制的。与Mg-Al-Zn系合金相比，ZX115 镁合金中的合金元素含量远不及AZ31 合金中的高，但其变形激活能却与AZ91 合金的更为接近。其原因可能是由于ZX115 镁合金变形过程中动态析出的富Ca 相粒子的熔点高于Mg17Al12相的，从而对位错的钉扎及形变的阻碍作用更为突出，这也正是含Ca 镁合金高温蠕变性能相对较好的主要原 因[1]。

3 热压缩的DEFORM 模拟

将以上拟合的ZX115 合金热压缩过程的本构方程(式(4))导入有限元模拟软件DEFORM 3D，建立ZX115 鲜合金的材料库，可用于合金的挤压、轧制、压缩等塑性变形过程的模拟与分析。在本实验中主要模拟ZX115 镁合金的热压缩过程，分析研究试样在温度350 ℃、应变速率1 s-1下压缩至真应变0.7 时的应变、应变速率、温度和应力等分布及变化情况。模拟试样尺寸与实验试样相同(d 10 mm×15 mm)，选取圆柱体试样的1/4 进行模拟运算。

3.1 应变场分布及变化

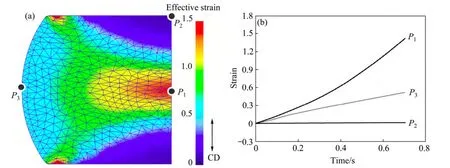
图6 试样压缩至应变量0.7 时的应变分布及应变随时间的变化曲线(350 ℃, 1 s-1) Fig. 6 Distribution of strain in simulated sample compressed to strain of 0.7(a) and change curves of strain with time(b) (350 ℃, 1 s-1)

图6(a)所示为ZX115 镁合金压缩后的应变分布， 其中垂直方向为压缩方向CD。由图6(a)可以看出，压缩后，试样内应变分布很不均匀，这是由于试样端面与压头之间的摩擦造成试样的不均匀变形引起的。其中，压缩试样中心区域应变值相对较大(如P1点，应变值为1.40)，与压缩砧头接触的圆面中心处应变值最小(如P2点，应变值仅为0.014)，而试样圆柱面由于鼓肚现象的存在，其应变状态较为复杂(如P3点，应变值为0.52)。

对上述3 个典型位置的应变值进行追踪分析，以考察其应变值随时间增加的变化情况，结果如图6(b)所示。在压缩初期，不同位置的应变值增加均比较缓慢，各处的应变相差不大；随着时间的延长，P1点处应变增长速率最快且数值最大(网格畸变严重)，P3点处应变值则呈线性增长，而P2点处应变值基本不发生变化(网格基本无畸变)，此位置试样未发生明显变形。可见，试样压缩过程中变形并不均匀。

一般认为，动态再结晶的初始形核与应变量有着密切关系。当变形量较小时，晶粒内因位错密度较小而难以发生动态再结晶，而当达到某一临界变形量时，才会发生动态再结晶形核。由模拟结果可以看出，压缩变形时P2处应变量一直很小，尚处于应力-应变曲线中的加工硬化阶段(见图1(c))，并未发生动态再结晶；随着变形时间的延长，P3处应变值达到并超过峰值应变0.32(见图1(c))，动态再结晶发生并逐步占据重要作用，导致应力-应变曲线下降；类似地，试样中心P1处在较短变形时间内即可发生动态再结晶，且随着应变的不断增加，再结晶晶粒亦可发生动态再结 晶[23]，因而，该区域的动态再结晶相对比较完全且再结晶晶粒更加细小。

3.2 应变速率、应力及温度场分布

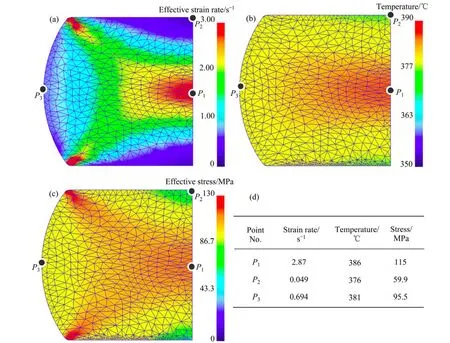
图7 热压缩至真应变0.7 时试样内应变速率、应力及温度分布的有限元模拟(350 ℃, 1 s-1) Fig. 7 FEM simulated distributions of strain rate, stress and temperature in sample compressed to true strain of 0.7 (350 ℃, 1 s-1): (a) Distribution of strain rate; (b) Distribution of stress; (c) Distribution of temperature; (d) Detail values for three typical points in compressed sample

压缩试样变形的不均匀性导致了试样内应变的不均匀分布，同时对试样内的应变速率、应力及温度场分布也产生了不同程度的影响，其结果如图7 所示。 同样选取3 个典型的区域进行分析，由图7 可以看出，应变速率、应力及温度场分布的不均匀特征与应变分布(见图6(a))相似，均表现为P1处的对应值最大，而P2处的值最小，具体的模拟数据如图7(d)所示。

值得注意的是，虽然压缩变形的应变速率设定为1 s-1，但当压缩至应变量0.7 时，试样内各处的应变速率却不尽相同(见图7(a))，P2处应变速率几乎为0，而P1处应变速率为2.87 s-1，约为初始设定值的3 倍，这与该处的应变迅速增长相对应。同样地，P1处的实际温度为386 ℃(见图7(b))，高于预热温度36 ℃，这是因为压缩变形中产生塑性变形所消耗的机械能大部分转变成热能，使试样内部温度升高。由此可以推断：试样的中心区域是在高温高速状态下进行压缩变形的，对其再结晶晶粒尺寸的预测并不能严格按照初始变形条件进行估算。也就是说，为了合理地控制再结晶晶粒尺寸，在不影响变形协调性和连续性的前提下，可适当考虑在稍低温度和稍低应变速率下进行形变。

由试样的应力分布(见图7(c))可以看出，部分红色区域的应力值大于该条件下压缩至应变量0.7 时的稳态应力值123 MPa(见图1(c))，但3 个典型区域P1～P3的应力值却均小于123 MPa。结合上述的应变速率、温度分布及图1 中的应力-应变曲线可知其原因，如P1处，其实际应变速率高于其预设值，有利于提高稳态应力值，而实际温度高于预设值则可降低稳态应力值，相比之下，温度对稳态应力值的影响大于应变速率的影响。当然，可能还会存在其他原因，有待在以后的研究中进行进一步的分析和证实。

4 结论

1) 含Ca ZX115 镁合金热压缩时的应力-应变曲线具有明显的动态再结晶特征，温度越高或应变速率越低时，流变曲线所达到的峰值应力越小，而在相同的应变速率下，峰值应变也随着变形温度的升高而明显减小。

2) ZX115 镁合金塑性变形过程中的流变应力、应变速率和变形温度之间的关系可用双曲正弦函数ε˙= A[sinh(ασ)]nexp[-Q/(RT)]表示，其中Q≈173 kJ/mol、α= 0.016 MPa-1、n=3.50。

3) ZX115 镁合金中高熔点的富Ca 相的存在对位错的钉扎及形变的阻碍作用更为明显，从而导致合金具有较高的变形激活能。

4) ZX115 镁合金的本构方程可应用于DEFORM 3D 有限元模拟，模拟结果表明：ZX115 镁合金热压缩过程具有明显的变形不均匀性，由于变形过程中局部温度和应变速率明显增加，为了合理控制变形后的再结晶晶粒尺寸，可适当降低形变温度和应变速率。

[1] HONO K, MENDIS C L, SASAKI T T, OH-ISHI K. Towards the development of heat-treatable high-strength wrought Mg alloys[J]. Scripta Materialia, 2010, 63(7): 710-715.

[2] SOMEKAWA H, MUKAI T. High strength and fracture toughness balance on the extruded Mg-Ca-Zn alloy[J]. Materials Science and Engineering A, 2007, 459(1/2): 366-370.

[3] SUN Y, ZHANG B P, WANG Y, GENG L, JIAO X H. Preparation and characterization of a new biomedical Mg-Zn-Ca alloy[J]. Materials Design, 2012, 34: 58-64.

[4] HOMAYUN B, AFSHAR A. Microstructure, mechanical properties, corrosion behavior and cytotoxicity of Mg-Zn-Al-Ca alloys as biodegradable materials[J]. Journal of Alloys and Compounds, 2014, 607: 1-10.

[5] 欧阳春, 雷 霆, 王 丽, 李年丰, 周乐山. Mg-Zn-Ca 三元镁合金生物材料的腐蚀行为[J]. 中国有色金属学报, 2010, 20(5): 891-897. OUYANG Chun, LEI Ting, WANG Li, LI Nian-feng, ZHOU Le-shan. Corrosion behaviours of ternary Mg-Zn-Ca alloy biomaterials[J]. The Chinese Journal of Nonferrous Metals, 2010, 20(5): 891-897.

[6] LARIONOVA T V, PARK W W, YOU B S. A ternary phase observed in rapidly solidified Mg-Ca-Zn alloys[J]. Scripta Materials, 2001, 45(1): 7-12.

[7] STANFORD N. The effect of calcium on the texture, microstructure and mechanical properties of extruded Mg-Mn-Ca alloys[J]. Material Science and Engineering A, 2010, 528(1): 314-322.

[8] 王天一, 丁汉林, 刘育峰, 魏 峰, 张义伟, 程广萍. Mg-1.0Zn-1.5Ca 合金热压缩过程的显微组织及动态再结晶行为研究[J]. 中国有色金属学报, 2014, 24(10): 2474-2481. WANG Tian-yi, DING Han-lin, LIU Yu-feng, WEI Feng, ZHANG Yi-wei, CHENG Guang-ping. Study on microstructure and dynamic recrystallization of Mg-1.0Zn-1.5Ca alloy during hot compression[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(10): 2474-2481.

[9] 丁汉林, 王天一, 徐成志, 李殿凯. Ca 添加及变形条件对Mg-Zn 合金组织与织构影响的研究[J]. 中国有色金属学报, 2015, 25(5): 1142-1152. DING Han-lin, WANG Tian-yi, XU Cheng-zhi, LI Dian-kai. Effects of Ca addition and deformation conditions on microstructure and texture of Mg-Zn alloy[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(5): 1142-1152.

[10] 王忠堂, 张士宏, 齐广霞, 王 芳, 李艳娟. AZ31 镁合金热变形本构方程[J]. 中国有色金属学报, 2008, 18(11): 1977-1981. WANG Zhong-tang, ZHANG Shi-hong, QI Guang-xia, WANG Fang, LI Yan-juan. Constitutive equation of thermal deformation for AZ31 magnesium alloy[J]. The Chinese Journal of Nonferrous Metals, 2008, 18(11): 1977-1981.

[11] CERRI E, LEO P, DE MARCO PP. Hot compression behavior of the AZ91 magnesium alloy produced by high pressure die casting[J]. Journal of Materials Processing Technology, 2007, 189(1): 97-106.

[12] HE Y B, PAN Q L, CHEN Q, ZHANG Z Y, LIU X Y, LI W B. Modeling of strain hardening and dynamic recrystallization of ZK60 magnesium alloy during hot deformation[J]. Transactions of Nonferrous Metals Society of China, 2012, 22(2): 246-254.

[13] 王宏伟, 易丹青, 王 斌, 蔡金伶, 钱 锋, 陈缇萦. Mg-6.3Zn-0.7Zr-0.9Y-0.3Nd 镁合金的高温塑性变形行为的热压缩模拟[J]. 中国有色金属学报, 2010, 20(3): 378-384. WANG Hong-wei, YI Dan-qing, WANG Bin, CAI Jing-ling, QIAN Feng, CHEN Ti-ying. Hot compressive deformation simulation of Mg-6.3Zn-0.7Zr-0.9Y-0.3Nd magnesium alloy at elevated temperatures[J]. The Chinese Journal of Nonferrous Metals, 2010, 20(3): 378-384.

[14] SELLARS C M, TEGART W J M. On the mechanism of hot deformation[J]. Acta Metallurgica, 1966, 14(9): 1136-1138.

[15] MCQUEEN H J, RYAN N D. Constitutive analysis in hot working[J]. Materials Science and Engineering A, 2002, 322(1): 43-63.

[16] RAVI-KUMAR N V, BLANDIN J J, DESRAYAUD C, MONTHEILLET F, SUÉRY M. Grain refinement in AZ91 magnesium alloy during thermomechanical processing[J]. Materials Science and Engineering A, 2003, 359(1/2): 150-157.

[17] ZHOU Hai-tao, WANG Qu-dong, WEI Yin-hong, DING Wen-jiang, ZHU Yan-ping, CHINO Y, MABUCHI M. Flow stress and microstructural evolution in as rolled AZ91 alloy during hot deformation[J]. Transactions of Nonferrous Metals Society of China, 2003, 13(6): 1265-1269.

[18] SPIGARELLI S, EL MEHTEDI M, CABIBBO M, EVANGELISTA E, KANEKO J, JÄGER A, GARTNEROVA V. Analysis of high-temperature deformation and microstructure of an AZ31 magnesium alloy[J]. Materials Science and Engineering A, 2007, 462(1/2): 197-201.

[19] ZHOU H T, LIU L F, WANG Q D, ZHU Y P, DING W J. Strain softening and hardening behavior in AZ61 magnesium alloy[J]. Journal of Material Science Technology, 2004, 20(6): 691-693.

[20] LIU Liu-fa, DING Han-lin. Study of the plastic flow behaviors of AZ91 magnesium alloy during thermomechanical processes[J]. Journal Alloys and Compounds, 2009, 484(1/2): 949-956.

[21] MYSHLYAEV M M, MCQUEEN H J, MWEMBELA A, KONOPLEVA E V. Twinning, dynamic recovery and recrystallization in hot worked Mg-Al-Zn alloy[J]. Materials Science and Engineering A, 2002, 337(1/2): 121-133.

[22] MOREAU G, Cornet J A, CALAIS D. Acceleration de la diffusion chimique sous irradiation dan sle systeme aluminium-magnesium[J]. Journal of Nuclear Materials, 1971, 38 (2): 197-202.

[23] DING Han-lin, LIU Liu-fa, KAMADO S, DING Wen-jiang, KOJIMA Y. Investigation of the hot compression behavior of the Mg-9Al-1Zn alloy using EBSP analysis and a cellular automata simulation[J]. Modelling and Simulation in Materials Science and Engineering, 2009, 17(2): 025009.