基于北斗卫星的缓和曲线信息列车运行综合地图匹配方法研究

李卫东，侯丽虹

(大连交通大学 电气信息学院，辽宁 大连 116028)＊

0 引言

列车定位系统是列车控制系统的核心单元，因此对列车的实时控制和定位显得尤为重要.地图匹配算法可以分为两个相对独立的步骤:一是找到列车当前正在行驶的路线;二是将列车当前的定位点匹配到轨道上［1］.

地图匹配算法按照空间区域关系可以大致分为两类:确定性算法和不确定性算法.投影法是一种确定性算法，相对简单，易于实现，但是效率较低，稳定性较差.最小二乘曲线拟合法是一种基础的匹配方法，优点是模型简单，实时效果好，但是误差较大，精度不高.

针对单一的匹配算法存在定位精度不高、可靠性差的问题，本文将确定性算法和不确定性算法相互结合，提出了基于三次B样条曲线拟合的综合地图匹配方法.该方法的优点是只利用了北斗卫星测量的经度和纬度信息，就可以拟合出列车的行驶路线，不需要使用其他的辅助测量设备，而且B样条曲线具有几何不变性、连续性、对称性和递推性等特性［2］可以方便地对拟合曲线进行局部修正.实验证明，该方法能够有效的实现地图匹配.

1 三次B样条曲线拟合的原理

铁路线路主要由直线段、圆曲线和缓和曲线组成，直线与圆曲线之间通过缓和曲线过渡，我国铁路采用的缓和曲线属于三次曲线［3］.选择三次B样条曲线进行拟合，可以同时满足不同轨道的要求，而且拟合的曲线更加平滑，拟合效果更加贴近实际情况.B样条曲线的定义是，给定n+1个平面的或空间的顶点Pi(i=0，1，…，n)，称n 次参数段:

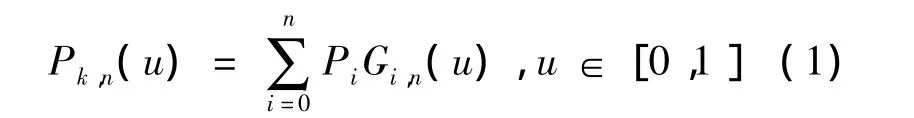
为第k段n次B样条曲线，Gi，n(u)是n次B样条曲线的基函数，其顶点Pi所组成的多边形称为B样条曲线的特征多边形.

图1 三次B样条曲线示意图

由B样条曲线的定义可知，第k段n次B样条曲线只与n+1个控制顶点Pi有关.如图1所示，6个控制顶点Pi控制的三次B样条曲线由三段B样条曲线段组成.其中，每一条曲线段由4个顶点Pi控制.B样条曲线具有局部性，在改动其中一个控制顶点时，只会对相邻的n+1段产生影响，不会对整条曲线产生影响.因此，B样条曲线的局部性质在实际应用中非常重要，可以对列车行驶路线进行局部调整提高匹配精度.

取n=3则有三次B样条曲线段Pi，3(u)，其中 (i=0，1，2，3):

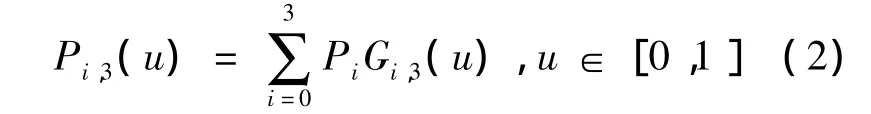
三次B样条曲线的基函数如下:

写成矩阵形式为:

其中:G为三次B样条的基函数矩阵;X，Y分别是每段三次B样条曲线控制顶点的坐标向量，(xu，yu)为三次B样条曲线上的点.随着u连续的取值，就能绘制出一段光滑的B样条曲线.当有n个控制顶点时，只需要将控制顶点移动n-3次，就可以获得完整的三次B样条曲线.

2 三次B样条曲线拟合匹配算法的实现

2.1 坐标系的转换

我国北斗定位系统采用的是CGCS2000坐标系，而在实际应用中GIS数字地图采用的主要是BJ-54坐标系［4］.因此，北斗卫星测量的结果不能直接使用，必须经过相应的坐标转换.本文采用三参数转换法，将CGCS2000坐标系统转换到BJ-54坐标系，其转换参数可以采用WGS-84坐标系统到BJ-54坐标系统的转换参数，在坐标变换的过程中不可避免的会产生一些误差，一般认为由坐标转换带来的误差不超过10 m［5］.本文将北斗卫星测得的经纬度信息转换成公里标的结果如表1所示.

表1 坐标转换结果

2.2 确定列车行驶的路线

在实际应用中，往往只知道北斗卫星定位系统经过预处理的数据点集 {Qi，(i=1，2，…，n-1)}，这些数据点是B样条曲线上的型值点，而并不是构成特征多边形的顶点，为了构造B样条曲线，就需要由这些型值点反求出特征多边形的控制顶点 {Pi，(i=0，1，…，n)}.由曲线端点的性质可知:

该方程组有n-1个方程，n+1个未知数，因此需要利用端点切矢m0和mn，补充两个边界条件才能求解.补充的两个边界条件:

写成矩阵形式有:

反求出控制顶点后，再利用上文给出的三次B样条曲线段公式(4)和已知的型值点Qi，就可以拟合出列车行驶的路线.如图2所示，可以清楚的看到，北斗卫星实时接收的实测数据点Qi和拟合曲线基本重合.

图2 列车行驶轨迹三次B样条拟合曲线

2.3 确定列车的位置

铁路线路是由一系列简单的基本元素构成的复合曲线，将直线、缓和曲线和圆曲线按照不同的组合方式相互连接，可以构成不同的线路结构.常见的是两端带缓和曲线的组合形式，按直线段1——缓和曲线段 1——圆曲线——缓和曲线段2——直线段 2顺序组合构成.如图3所示，ZH(直缓)、HY(缓圆)、QZ(曲中)、YH(圆缓)、HZ(缓直)为曲线的五个主点.

图3 铁路线路组成平面示意图

在列车行驶的线路中，无论是直线、圆曲线、缓和曲线中的任一种线元，都可以分割成无限个小区间合成的曲线.只需要知道列车行驶轨道起点和终点的坐标，运行里程，方位角以及曲率半径，就可以利用复化梯形公式方便地计算出该段线元上任意点的坐标和方位角.

图4 定位点匹配原理图

如图4所示，ZH是曲线段的起点，其坐标值(xZH，yZH)，行驶里程DZH和航向角θZH已知.Q点是获取的当前时刻列车位置，ZH和Q点连线与ZH点切线lZH夹角α≤90°，并且曲线段终点HZ和Q点连线与HZ点切线lHZ夹角β≥90°，可以判断出Q点位于曲线段内部.

由Q点向ZH点切线lZH作垂线，垂足是P1，与曲线段的交点是A.HY点的里程近似为DHY=DZH+ZHP1，由复化梯形式(9)，可以求出HY点的坐标和方向角.同理，连接HY和Q点，lHY是HY点的切线，由Q点向lHY作垂线，垂足是P2，与曲线段的交点是B.以此类推，经过n次计算，最终可以得到Q点在曲线段上的投影点W的坐标，WQ与W点切线lW的夹角φ=90°.

式中:h=(Di-DZH)/n;φZH是曲线段起点ZH切线方向角;φk是曲线段n等分点处的切线方向角;φi是曲线段上待求点处的切线方向角，φi可以通过式(10)和(11)求解.

式中，Di是曲线段上待求点的里程;ρi是曲线段上待求点的曲率.上式 ±取值说明:以里程数增大为前进方向计算时，曲线右转取 +，左转取 -;以里程数减小为前进方向计算时，曲线右转取-，左转取 +.

铁路线一般为曲线，上面包含车站、路径的线段端点、整公里标点、道岔点等，这些点统称为标识点.列车轨道上每间隔500 m或者1 000 m会设置一个标识点，基于GIS的上位机通过北斗Ⅰ+Ⅱ标签上传的坐标点与铁路电子地图的这些标识点匹配实现位置显示.在一个投影点的附近可能有多个标识点，将计算结果与电子地图的标识点坐标对比，距离最接近的就是列车的实际运行位置.

3 三次B样条曲线拟合的误差分析

本文采用的是哈尔滨西至长春运营线路的实测数据，列车最高时速200 km/h，平均车速为99.90 km/h.北斗Ⅱ卫星接收机设置2 s接收一次数据，以哈尔滨西站的经纬度坐标为起点基准位置，列车实际运行139.86 km，共采集了2 500个北斗Ⅱ卫星的测量数据点.

为了方便对该算法进行评判，本文定义了三个评价指标，分别是里程误差、误差均值和均方根误差.表2是实测数据的各项评价指标，计算公式如下:

里程误差:

误差均值:

均方根误差:

其中，ΔDi，i+1表示定位点Qi和Qi+1之间的里程，ΔDi，i+1=(vi+vi+1)/2ti，i+1，D 是 Q1到 Qn-1的里程D=× t.

表2 各项误差评价指标

北斗定位系统在有标校地区的定位精度一般优于10～20 m［6］，本系统将北斗卫星误差精度20m时的各项误差值作为误差评价的基准值.表2的数据表明，本系统根据实测数据计算得到的三个误差值，符合北斗定位系统的精度要求.

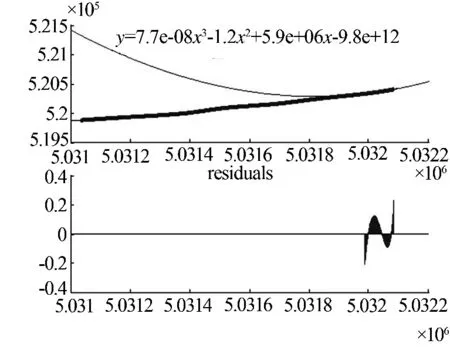
图5 三次B样条拟合曲线残差图

观察图5中的三次B样条拟合曲线的残差分布情况可知，本系统的残差曲线成下降趋势，残差范围是 -0.207 ～0.232.

4 结论

精确可靠的列车定位技术是列车安全运行的前提条件，也是高速铁路快速发展的重要保障.本文采用的是我国自主研制的北斗卫星定位系统，根据哈尔滨西至长春运营线路的部分测量数据，建立了基于三次B样条曲线拟合的电子地图匹配模型.实验结果表明，基于三次B样条曲线拟合的列车定位综合方法能有效提高列车定位的精度和可靠性，具有一定的实际意义.该算法可以准确的识别出运行速度为200 km/h的高速列车的行驶轨迹，判断出列车的具体位置，误差精度符合电子地图匹配的要求，并且残差可以控制在-0.207～0.232的范围内.增强了定位系统的适应能力，适用于铁路交通运输的控制和管理.

［1］李晓峰.车载定位导航系统地图匹配算法设计与实现［J］.嘉应学院学报，2010(11):79-82.

［2］陈露.基于特征性质的三次B样条拟合算法［D］.大连:大连理工大学，2009.

［3］汪俊.基于GNSS的列车定位系统中数字轨道地图的研究［D］.北京:北京交通大学，2010.

［4］廖永生，陈瑞波，王龙波.从地方坐标系到2000国家大地坐标系的转换方法［J］.海洋测绘，2010(5):6-8.

［5］卢文涛，周银东，梅顺良，等.基于拓扑结构的地图匹配算法研究［J］.测控技术，2010(6):73-76.

［6］顾一中，孙亚民，王华，等.基于北斗定位系统的新型无线传感器网络路由算法［J］.兵工学报，2009(3):306-312.