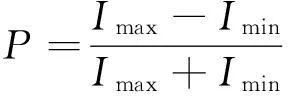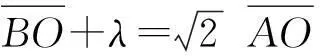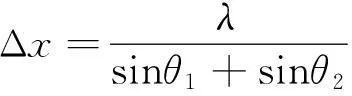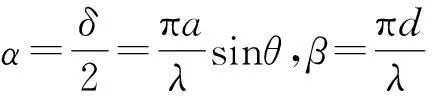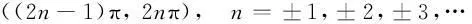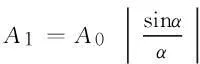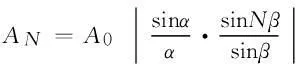光学教学中的几个问题

戴松涛

(清华大学物理系，北京　100084)



光学教学中的几个问题

戴松涛

(清华大学物理系，北京100084)

摘要本文首先讨论光的偏振态的分类与偏振度的定义,然后分析一个两束平行光干涉的问题,最后指出有些教材中关于单缝和多缝夫琅禾费衍射的振幅公式是不全面的，并给出正确公式.

关键词偏振态的分类；偏振度；两束平行光的干涉；衍射振幅公式

本文针对一些教材和某题解中的疏漏进行了分析和疏理，内容涉及光的偏振态的分类与偏振度的定义、两束平行光的干涉以及单缝和多缝夫琅禾费衍射的振幅公式.

1光的偏振态的分类与偏振度的定义

可以证明[1]：任意一束给定的准单色光，都可看成是一束非偏振光(自然光)与一束完全偏振光之和，并且这种分解是唯一的.由此可知，光的偏振态除了两种极端情形(非偏振光和完全偏振光)外，其他的情形都属于二者的混合，称为部分偏振光.因为完全偏振光(也叫纯偏振光，简称偏振光)可分为线偏振光、圆偏振光和椭圆偏振光[2, 3]，所以，认为部分偏振光是自然光和线偏振光的混合的观点[4, 5]是不全面的.造成这种疏漏的原因也许是一些常见的情形(如自然光斜射到两种介质的分界面时形成的反射光和透射光)属于这类部分偏振光.

由上述结论，可以自然地用一束光中完全偏振成分的强度Ip在该束光总强度It中所占比例来定义该束光的偏振度P[1, 2]，即

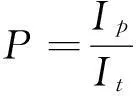
(1)

图1　光按偏振态的分类

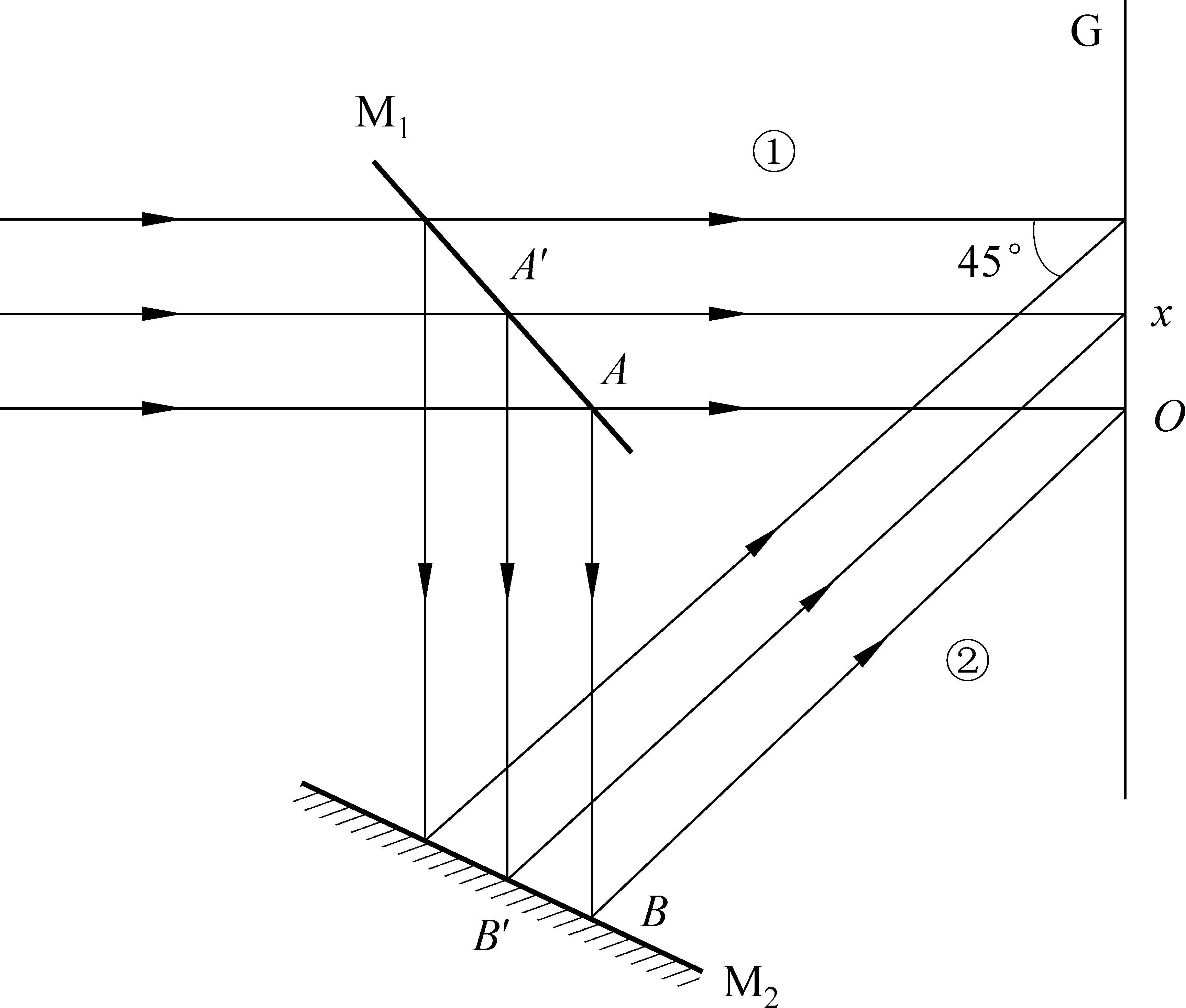
偏振度是光束偏振程度的量度，利用它可以自然地将光的偏振态分为3大类(简称三分法)：完全偏振光(P=1)、非偏振光(自然光，P=0)以及介于二者之间的部分偏振光(0

(2)

有些教材[4, 6, 7, 10]用式(2)作为偏振度的定义，但这是有局限性的[2, 11]，因为这种方法对于圆偏振光、椭圆偏振光以及由它们与自然光混合而成的部分偏振光是不适用的.

普遍适用的测量偏振度的方法[2]是“让光束先通过一块1/4波片，然后通过偏振片(如果只用偏振片时转动它而透射光强有变化，就应使1/4波片快轴或慢轴沿光强最大的振动方向)，再测透射光强.这样，无论待测部分偏振光原来包含的偏振成分是圆偏振、椭圆偏振或者线偏振的，经过 1/4 波片后都是同等强度的线偏振光.这时转动偏振片测得Imax和Imin”，就可用式(2)计算偏振度.“式中的Imax和Imin应理解为用一块1/4波片加一个线偏振器所能得到的最大和最小透射光强.”只有基于这种约定，式(2)与式(1)才是等效的.

2两束平行光的干涉

下面结合文献[12]中的一道习题(22.10)谈谈分析干涉现象时应注意的问题.如图2所示，M1为半镀银平面镜，M2为一反射平面镜.入射激光束一部分透过M1，直接垂直射到屏G上，另一部分经过M1和M2反射与前一部分叠加.在叠加区域两束光的夹角为45°，所用激光为632.8 nm.其中有一问是求在屏上干涉条纹的间距.文献[12]给出了如下的解答:

图2　文献[12]中的图23-7

而根据两束平行光干涉的条纹间距公式[4]

(3)

两种方法给出的结果如此不同，原因何在？从文献[12]的解答可以看出，作者忽略了M1的厚度，当然这并不影响相对光程差的计算.即便如此，

3单缝和多缝夫琅禾费衍射的振幅公式

有些教材[2, 4-7, 10]将单缝和多缝夫琅禾费衍射的振幅分布写成以下两式：

(4)

(5)

先来看式(4)，随着衍射角θ的变化，A1可正可负[13]，而简谐振动的振幅应是非负的[14-16]，在矢量图解法中它对应于合成矢量的模，这个矛盾是如何产生的？考察式(4)的推导过程[4]可知，它是由矢量图解法通过一个扇形的弦长导出的，如图3(b)所示.而该图形并未涵盖所有可能情况[13].如图4所示，当α处于以下区间的情形就与图3(b)不同：

图3 单缝夫琅禾费衍射(a)光程差分析(b)矢量图解法(引自文献[4])图4 由矢量图解法推导衍射振幅公式时应考虑的一种典型情况(引自文献[13])

综合考虑所有可能情况，式(4)应写成如下的更普遍形式[13]

(6)

基于类似的考虑，式(5)应写成如下的更普遍形式：

(7)

式(7)也可从另外的途径得到[17].

4结语

本文讨论了涉及偏振、干涉和衍射的若干概念和公式，分析了一些教材忽略的问题和某题解中的错误，指出了处理波的叠加时应注意的问题.

参考文献

[1]Born M, Wolf E. Principles of Optics [M]. 7th (expanded) edition. Cambridge: Cambridge University Press, 1999: 626, 628.

[2]牟绪程, 邓新元, 董文达. 波动与光学(下册) [M]. 北京：清华大学出版社，1994: 137, 162, 196-205, 289-291.

[3]潘维济. 光学问答 [J]. 大学物理, 1992, 11 (6): 7-8.

[4]钟锡华. 现代光学基础 [M]. 2版. 北京：北京大学出版社，2012: 59, 81, 98, 102, 104.

[5]张三慧. 大学物理学——光学、量子物理 [M]. 3版A版. 北京：清华大学出版社，2008: 26, 36, 47, 72.

[6]陈熙谋. 光学 [M]. 2版. 北京：北京大学出版社，2011: 15, 105, 116, 160.

[7]崔宏滨, 李永平, 段开敏. 光学 [M]. 北京：科学出版社，2008: 53, 96, 146.

[8]郭永康，朱建华，王磊，等. 光学 [M]. 北京：高等教育出版社，2005: 59, 103 -104.

[9]章志鸣，沈元华，陈惠芬. 光学 [M]. 2版. 北京：高等教育出版社，2000: 34.

[10]崔宏滨. 光学基础教程 [M]. 合肥：中国科学技术大学出版社，2013: 348, 446.

[11]吴健. 光学教学中的偏振度定义 [J]. 大学物理, 2005, 24 (10): 8-10.

[12]黄伯坚, 周逊选, 周述文. 大学物理学习题详解 [M]. 武汉：华中科技大学出版社，2002: 473-474.

[13]戴松涛. 衍射教学中的问题与思路 [C].//2011年全国高等学校物理基础课程教育学术研讨会论文集. 2011: 271-273.

[14]蔡伯濂. 力学 [M]. 长沙：湖南教育出版社，1985: 289.

[15]周乐柱，张耿民. 力学 [M]. 北京：北京大学出版社，2011: 140.

[16]李复. 力学教程(下) [M]. 北京：清华大学出版社，2011: 75.

[17]赵诗华，藤爱萍. 光栅衍射的初步分析 [J]. 大学物理, 2005, 24 (4): 55-57.

■

教学研究

SOME PROBLEMS IN OPTICS TEACHING

Dai Songtao

(Department of Physics, Tsinghua University, Beijing 100084)

AbstractIn this paper, the classification of polarization states of light and the definition of degree of polarization are first discussed. Then a problem on two parallel beam interference is analyzed. Finally, it is pointed out that the amplitude figuree for single-slit and multiple-slit Fraunhofer diffraction in some textbooks are incomplete, and the correct figuree are presented.

Key wordsclassification of polarization states; degree of polarization; two parallel beam interference; diffraction amplitude figuree

基金项目:清华大学本科教学改革项目(2014)资助.

作者简介:2015-10-17 戴松涛，男，主要从事物理教学与科研工作，研究方向为光物理.daist@tsinghua.edu.cn