粗糙涂层材料的偏振反射特性分析
曹昭斌,黄雁华,杨云涛,龚艳春,史冬冬,杨 军,武文远
(陆军工程大学,江苏 南京 211101)
1 引 言
当前,随着伪装、隐身材料及相关技术的发展,人们可将材料涂敷在人造金属目标表面上实现伪装,这使得传统的目标检测方式难以实现对伪装目标或隐身目标的精准识别。在复杂环境背景下,尽管涂有伪装涂层的人造目标可以实现强度特性或光谱特性的伪装,但是其偏振特性并不能实现很好地“伪装”。人们可以运用新型的目标检测手段——偏振技术,通过分析电磁波振动状态的变化从而获取物质的组成、类别及性质等重要信息,这些信息在伪装目标检测方面发挥着重要作用[1-2]。偏振探测技术是通过采集目标的偏振参量实现精确地探测[3-5],例如偏振度、线偏振度、偏振角等,它不仅可以高效地提高探测的精准度,而且相较于传统的探测方式能够使“强光弱化”,“弱光强化”,可以有效地提高目标与背景之间的对比度,在目标检测方面具有更好的效果[6]。
粗糙涂层本身的理化特性(如折射率、含水量、表面粗糙度、涂层厚度、涂层层数、消光比等)、入射角、探测角、方位角及光的性质等因素决定了光与其作用后的偏振特性[7-9]。我们通过探究不同因素对偏振特性的影响,可以筛选最优条件下的偏振参量,利用偏振信息可以有效地识别不同的伪装目标。2009年张朝阳等人研究了入射角、观测方位角对伪装涂层材料偏振散射特征的影响,有效地识别草地背景中的伪装目标[10]。2013年曹慧等人研究了多因素影响下两种典型涂层目标在微粗糙基底上的光散射偏振特性,分析了波长、入射角、探测角及涂层特性对偏振度的影响,表明光学厚度为λ/4的涂层目标偏振度最大[11]。2016年苏志强等人在考虑表面粗糙度的条件下,研究了石英玻璃和绿漆涂层的偏振度与探测天顶角间的关系[12]。2020年柳祎等研究了表面粗糙度和入射角对金属和非金属目标红外辐射偏振度的影响,利用红外偏振图像有效分辨了金属与非金属目标[13]。以上研究虽然探究了目标在不同因素下线偏振度的变化规律,但并未讨论S偏振光照射粗糙涂层后反射光的线偏振度峰值变化规律。
本文利用多角度高光谱偏振反射平台测量了S偏振光照射三种粗糙涂层反射的光强及斯托克斯参数,计算得到了400~1000 nm范围内涂层表面反射光的线偏振度,从连续波段中选取555 nm、670 nm及865 nm对应的线偏振度进行了数据分析,进一步地讨论了波长、入射角及探测角等因素对涂层材料线偏振度和线偏振度峰值的影响,并提出了针对粗糙涂层目标的检测方法。
2 Stokes矢量表示偏振度
1851年Stokes在其文中引入Stokes矢量[14]S=[I,Q,U,V]T描述光的偏振态,它可以表示包含在部分偏振光中的任意偏振光,在忽略微弱的圆偏振特性下,其各个参量表示为:
(1)
式中,ax、ay及δ分别表示x、y方向上电场的振幅及两者的相位差;〈〉表示求某一周期内参量的时间平均值;I表示光的总强度;Q表示水平方向上线偏振光的强度;U表示45°方向上线偏振光的强度。
当目标反射光束经与透光轴成θ的线偏振器后,探测器接收的光的Stokes参数变为:


(2)
分别取偏振片透光轴0°、45°、90°、135°后,只需求得探测器各个角度的光强,便可求得目标表面反射光束的Stokes参量:
(3)
利用所得的Stokes参量即可表示线偏振度(Degree of Linear Polarization,DoLP):
(4)
3 实验及结果分析
3.1 实验方法
本实验通过多角度高光谱偏振反射平台改变入射及探测角度,实现粗糙涂层偏振反射特性的参数测定。实验仪器主要由光源、线偏振片、精密机械旋转平台、光谱仪及计算机五部分组成,其中光源是卤素灯,波段范围为350~2500 nm;两个线偏振片分别安装在光源及探测器前,可获取不同偏振态的光;利用QE Pro光谱仪(波长范围:350~1100 nm;半峰全宽FWDM:0.7~2 nm;信噪比1000∶1)测得目标反射的光强值,实验原理如图1所示。

图1 实验测量原理图Fig.1 Experimental measurement principle diagram
实验对象为具有同一涂层材料和金属基底材料的不同粗糙度绿色样品,涂层材料按照不同粗糙度涂到铁质金属板表面,分别获得了G1、G2和G3样品,每块样品大小为150 mm×150 mm,厚度约为20 mm,其中涂层厚度约为40 μm,各样品的表面粗糙度参数如表1所示。

表1 涂层样品的表面粗糙度参数Tab.1 Surface roughness parameters of coated samples
实验在暗室室温25 ℃、相对湿度30 %、入射方位角φi=180°和探测方位角φr=0°不变的情况下进行,通过调整入射光处偏振片透光轴方向使得入射光为S偏振光,其透光轴方向垂直于主平面(图1的yoz平面)。光源固定在入射角θi转臂上,可手动调节,精度0.5°,并利用步进电机转动探测器转臂改变探测角θr的大小实现多角度测量,精度0.05°。在确定角度之后,旋转探测器位置处的线偏振片透光轴方向至0°、45°、90°及135°,并配合光谱仪及计算机配置的Oceanview软件采集各个偏振方向下的光强信息,运用公式(3)可计算求得S光照射涂层表面后的Stokes参数I、Q及U,并利用公式(4)求得涂层表面反射光的DoLP信息。
3.2 波长对DoLP的影响分析
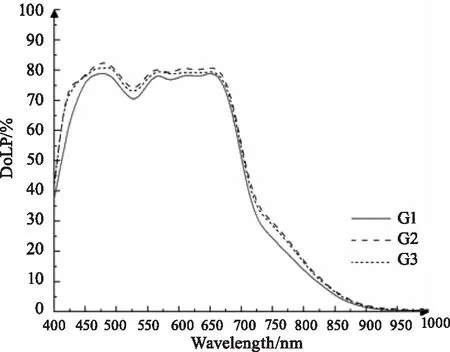
以S偏振光照射三种涂层,在入射光方位角180°、探测光方位角0°和镜面反射(即入射角与探测角相同)条件下,研究了400~1000 nm波长范围内的DoLP随波长的变化关系,实验曲线如图2所示。

(a)θi=θr=20°

(b)θi=θr=30°
(c)θi=θr=40°
由图可知:(1)粗糙涂层的DoLP与波长有较强的依赖关系,它随着波长的变化先增大后减小再增大,450 nm附近存在极大值点,525 nm附近有极小值;之后DoLP随着波长先减小后增大再急剧减小,600 nm处存在极小值,670 nm附近有极大值;865 nm后的DoLP不断减小,几乎趋近于0。这些规律表明可见光范围内涂层的线偏振度大于近红外波段的线偏振度,这是由于S偏振光的反射率与波长密切相关,不同波长下样品表面反射率影响了各个偏振态的光强值,继而改变了线偏振度数值。(2)相较于波长的影响,粗糙度并不会改变线偏振度极值点的位置,它只会改变线偏振度数值的大小。其中,G1样品对应的线偏振度值相较于其他样品最小,但三者的极小值点均在525 nm附近,其他极值点位置与(1)的描述接近一致。
3.3 入射角对DoLP的影响分析
从上述连续谱线中选取了常见的地物检测波长555 nm、670 nm及865 nm进行目标特性分析,在给定波长和探测角的条件下,测量不同入射角下样品的DoLP值,DoLP随入射角的变化关系如图3~5所示。



图3 θr=20°时,不同入射角下的DoLP柱状图Fig.3 DoLP histograms at different incident angles when


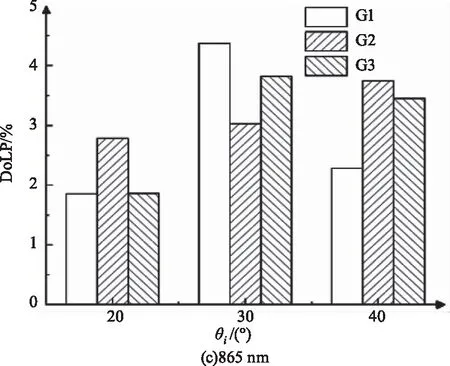
图4 θr=30°时,不同入射角下的DoLP柱状图Fig.4 DoLP histograms at different incident angles



图5 θr=40°时,不同入射角下的DoLP柱状图Fig.5 DoLP histograms at different incident angles
通过分析柱状图可得:(1)G1样品:在入射角θi=30°时,555 nm或670 nm(图(a)和图(b))处的DoLP数值有极小值,而865 nm处(图(c))的DoLP为极大值;(2)G2样品:555 nm和670 nm(图(a)和图(b))波长下,DoLP在θi=θr=20°时有最大值,而θr=30°、θr=40°不变时,DoLP值在θi=30°时有极小值。G2样品在865 nm处的DoLP均随着入射角增大而增大;(3)G3样品:三个波段下的DoLP值在θi=30°时均为极大值。(4)555 nm和670 nm处的三种样品的DoLP数值均在60 %~85 %范围内,而865 nm处的DoLP数值在5 %以下,表明可见光波段的线偏振度强于近红外波段。结合菲涅尔公式可知,同一波长下的S偏振光在不同入射角下的反射率不同,这一规律造成同一样品在相同波段下的线偏振度随入射角的变化而不同。而且在相同探测条件下,三种不同粗糙度的涂层材料表面反射光的线偏振度变化有明显的不同,表明粗糙度会影响样品表面反射光的偏振特性。
3.4 探测角对DoLP影响分析
在固定其他因素不变情况下,选取三个入射角度(20°、30°、40°),每间隔10°改变探测角,分别测得特定入射角下探测角在0°~60°范围内的DoLP信息,图6~8分别对应G1~G3样品的DoLP曲线图,(a)、(b)、(c)分别对应三个入射角度。



图6 不同探测角下G1的DoLP变化曲线图Fig.6 DoLP change curve of G1 under different detection angles
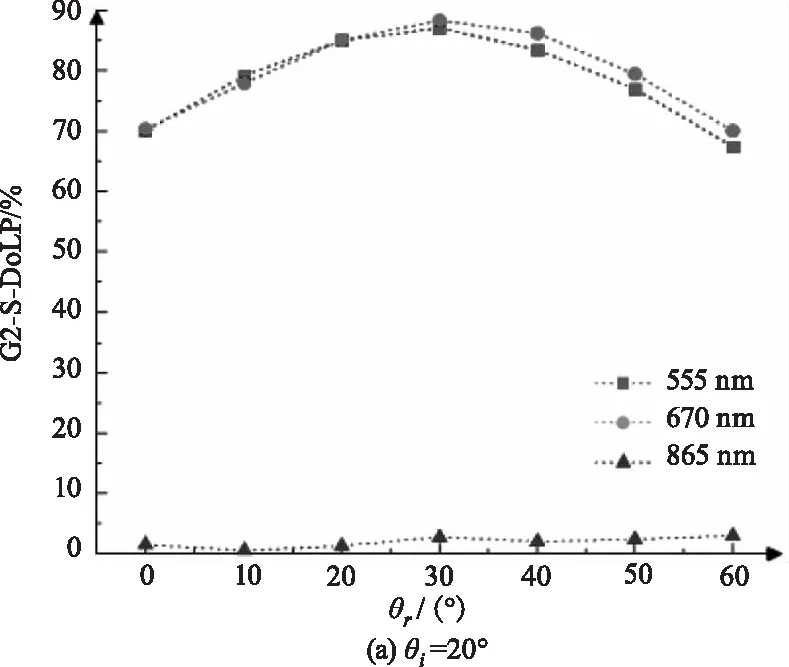
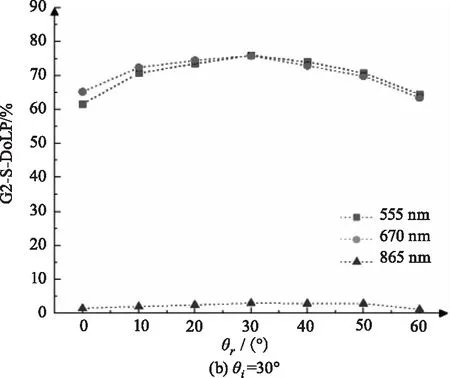

图7 不同探测角下G2的DoLP变化曲线图Fig.7 DoLP change curve of G2 under different detection angles

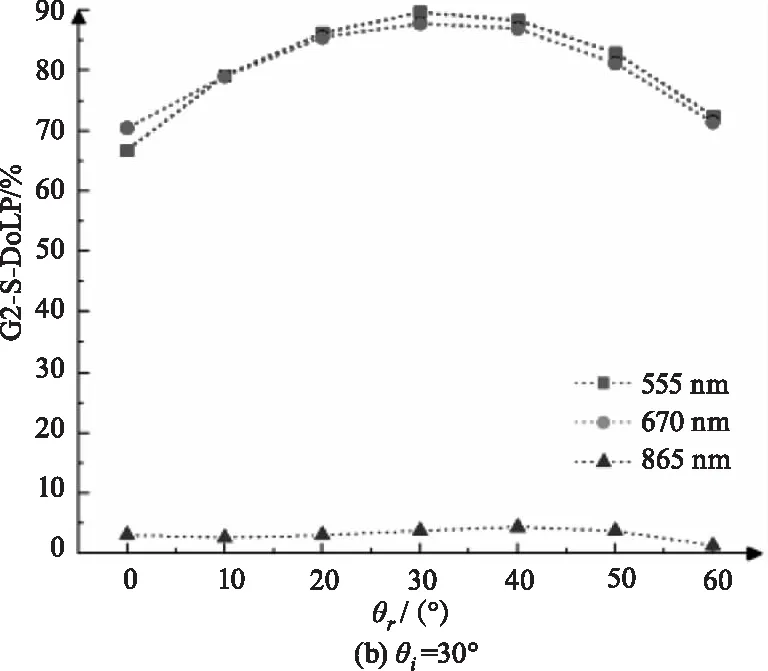
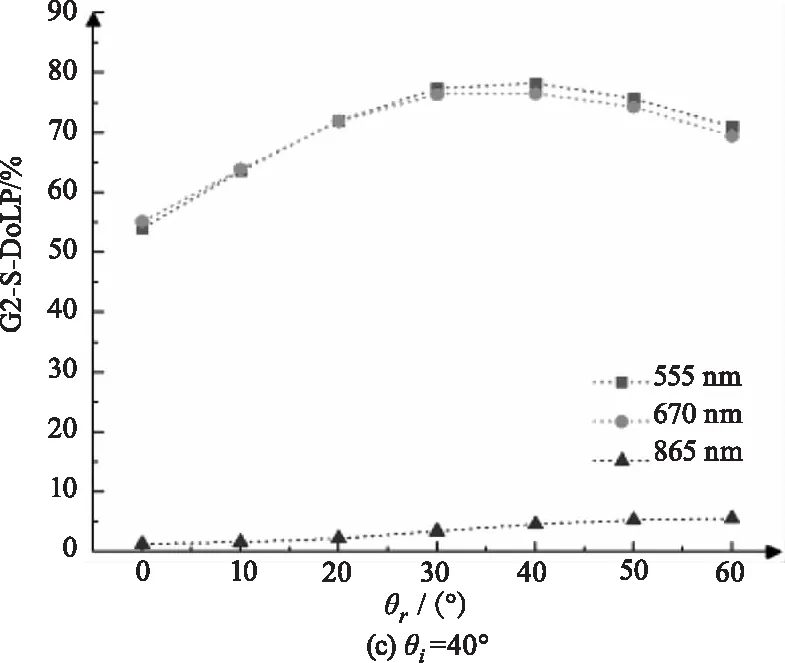
图8 不同探测角下G3的DoLP变化曲线图Fig.8 DoLP change curve of G3 under different detection angles
分析曲线可知:(1)粗糙涂层的线偏振度与探测角有密切联系,555 nm和670 nm对应曲线的变化趋势一致,即随着探测角增大,DoLP数值先增大后减小且小探测角处670nm的线偏振度均大于555 nm处的线偏振度,而865 nm的DoLP大体与探测角正相关,即随着探测角增大而增大;(2)555 nm及670 nm时,DoLP峰值大多会出现在镜面反射角附近,其中最小粗糙度的G3样品的现象最为明显,如图8所示:θi=20°时,(a)图DoLP峰值对应的探测角为20°;θi=30°时,(b)图峰值DoLP对应的探测角为30°;θi=40°时,(c)图DoLP峰值对应的探测角为40°,表明小粗糙度下,涂层表面反射光的线偏振度在镜面反射处最大。
3.5 影响DoLP的综合因素分析
上述讨论了单因素条件下涂层DoLP特性的变化规律,进一步地发现,波长、入射角和探测角的综合作用下,DoLP峰值呈现一定的变化规律:
(1)555 nm和670 nm波长下,DoLP峰值位置与入射光角度正相关,即入射角增大时,DoLP峰值位置向大探测角方向移动,如图6~8所示,这一现象的出现是由于镜面反射角附近的线偏振度最大,随着入射角的增大,镜面反射角同时变大,DoLP峰值位置向镜面反射角附近移动。
(2)粗糙涂层的线偏振度峰值在特定入射角及波长下存在极大值,如图6~8所示,在入射角小于30°时,670 nm峰值的线偏振度大于555 nm峰值的线偏振度,相反入射角大于30°时,670 nm峰值处的线偏振度小于555 nm的线偏振度。其中,图(a)入射角20°、670 nm的DoLP峰值明显大于555 nm,图(b)30°入射时两者近似相等,图(c)40°入射时670 nm的DoLP峰值小于555 nm。因此选取合适入射角和波长可获得较高的线偏振度。
结合上述规律,本文提出针对该粗糙涂层的检测方法:在S偏振光的入射角小于30°时,探测器在镜面反射角附近选取670 nm波长进行线偏振度检测,大于30°时选取555 nm波长可有效提高检测伪装涂层的精准度。同时,在确定波长、入射角及探测角的最优条件后,我们可进一步根据峰值处线偏振度值的大小,区分涂有同一涂层的粗糙的绿色伪装目标。
4 结 论
本文对三种不同粗糙度的绿色涂层材料的线偏振度进行测量,获得了S偏振光照射粗糙涂层表面后反射光的线偏振度变化规律,分析了波长、入射角及探测角等因素对线偏振度的影响:
(1)线偏振度与波长关系:粗糙涂层在小入射角度下,可见波段的线偏振度明显大于近红外波段,这一规律与涂层自身特性密切相关;(2)线偏振度与探测角关系:555 nm和670 nm处涂层表面反射光的线偏振度随着探测角增大先增大后减小,865 nm波长的线偏振度与探测角正相关;(3)线偏振度与粗糙度关系:粗糙度只会改变线偏振度数值大小,而不会改变线偏振度极值点的位置;(4)线偏振度峰值与影响因素关系:当探测角位于镜面反射角附近时,小粗糙度涂层表面的线偏振度出现峰值,其峰值位置与入射角正相关,并且线偏振度峰值大小与波长密切相关。
以上实验结论证明线偏振度可以作为检测粗糙绿色涂层的指标,同时合理地选取波长及探测条件可获取涂层的最大线偏振度,利用峰值处的线偏振度可有效提高检测的精准度,这对复杂背景下的偏振检测具有重要的应用价值。

