基于偏振度的目标微观表面偏振特性分析

刘 燕，张 健，邹 昕

（西北工业大学明德学院信息工程学院，西安 710124）

1 引 言

自20世纪80年代以来，偏振成像技术作为一种探测手段开始用于目标的有效识别，偏振光学信息很好地补充了目标的光强和光谱信息，提高了有效识别目标的能力。近几年来，科研人员利用空间目标的光度和光谱信息反演目标的空间位置、姿态和材料等信息。空间目标的偏振信息同样也包含了目标的姿态、位置和材料等信息，并且在传播过程中偏振信息的抗干扰抗衰减能力皆优于光度和光谱信息，因此利用空间目标的偏振特性反演识别目标，具有十分现实的应用价值，是非常有意义的事情[1-5]。故此，基于微面元理论的T-S BRDF 模型与菲涅耳反射穆勒矩阵得到偏振双向反射函数pBRDF 的表达式，再通过pBRDF 得到偏振度，进而分析偏振度随材料复折射率、入射角及观测角度的变化规律，旨在为后续从宏观层面分析目标几何形状、材料、相对位置对目标偏振度的影响提供一定的参考，为后续偏振度反演空间目标的材料、几何特性提供基础。

2 偏振双向反射分布函数模型

2.1 BRDF模型

BRDF（即双向反射分布函数，全称bidirectional reflectance distribution function）模型给出了物体表面光散射的空间分布。BRDF的基本概念和物理意义参考文献[6-8]，它的一般定义通常由下式表示：

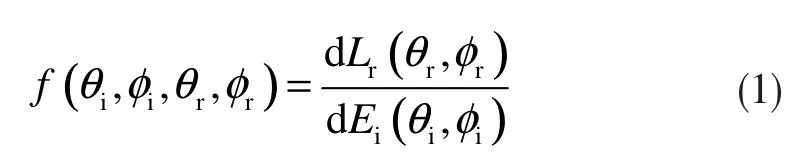
它的取值范围为零到无限大，单位sr-1。BRDF是一个微分量，不能直接测量。图1表示BRDF的几何关系。其中，θi、φi表示入射光的天顶角和方位角，θr、φr表示探测光的天顶角和方位角。

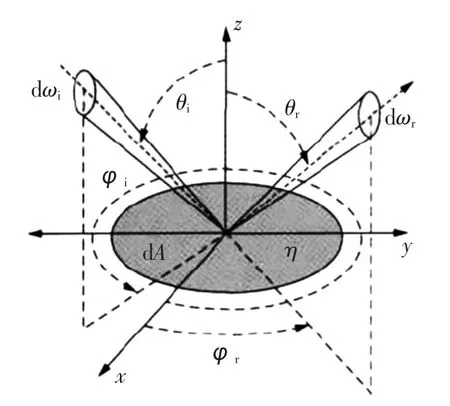
图1 BRDF几何关系图

推导基于已经成功应用于遥感探测中的T-S BRDF模型，其基本概念和物理意义见参考文献[9-10]。如图2所示为物体表面法线z及微面元法线zμ之间的相对位置关系。

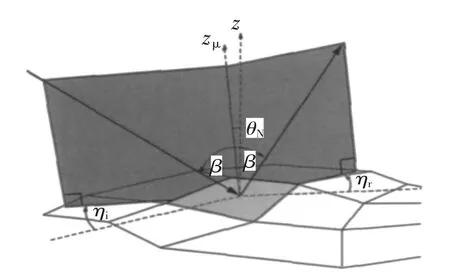
图2 微面元几何分布图

T-S BRDF模型可由如下各式来描述：

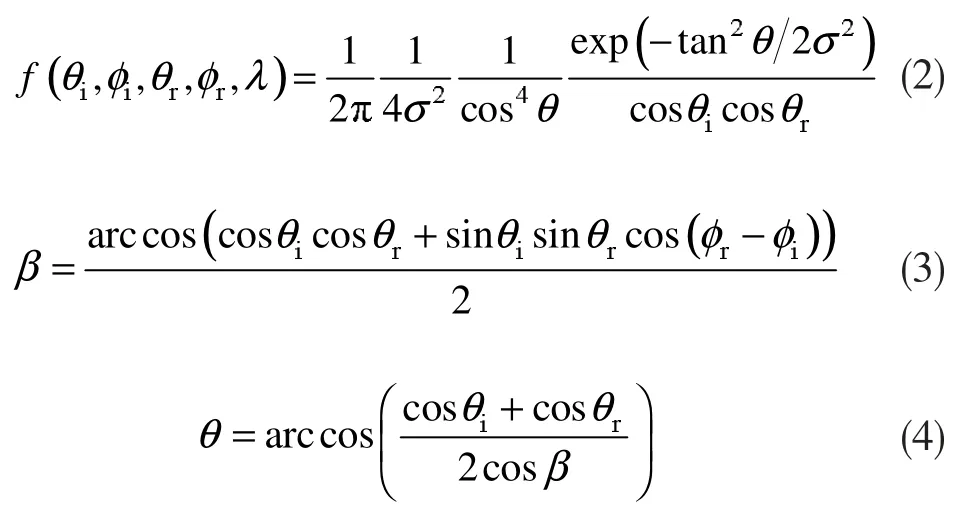
其中σ表示物体材料表面的粗糙度。式(3)中的β为入射方向与zμ间的夹角；式(4)中的θ为z与zμ间的夹角，即图2中的θN。

2.2 偏振双向反射分布函数

基于微面元理论的T-S BRDF模型与菲涅耳反射穆勒矩阵可以得到偏振双向反射函数（pBRDF）的表达式。计算穆勒矩阵需要计算偏振分量s、p的菲涅耳反射率Rs、Rp。这里s、p分别代表电场分量平行和垂直于探测面。由菲涅耳反射定律可知，材料表面的反射率是材料复折射率n+ik及入射角的函数，可由下式来描述：

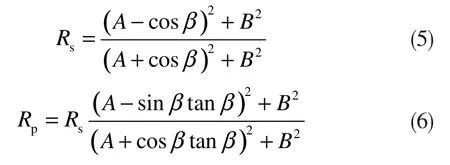
其中：

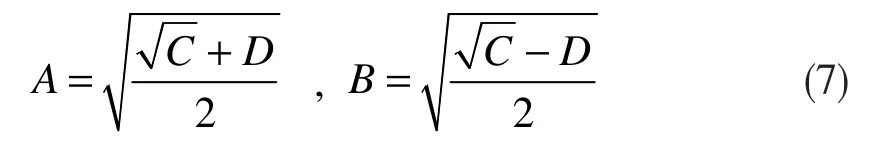
其中：

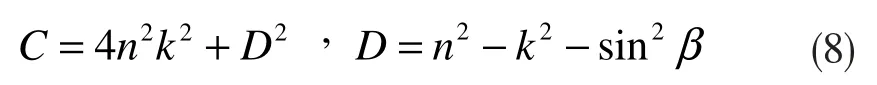
如图2中所示，入射方向、法线z、微面元法线zμ和探测方向相互组合构成4个参考平面，ηi、ηr为参考平面之间转换的夹角，表达式为：

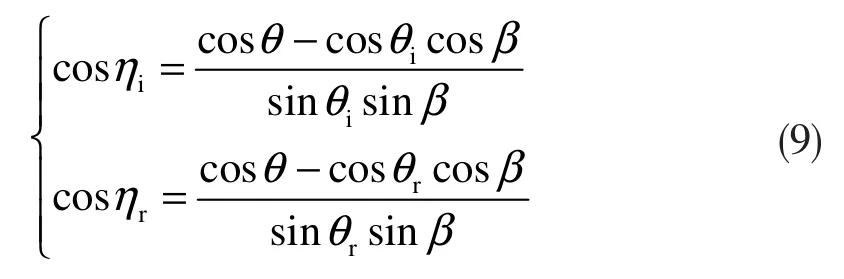
反射辐射的琼斯矩阵表达式为：

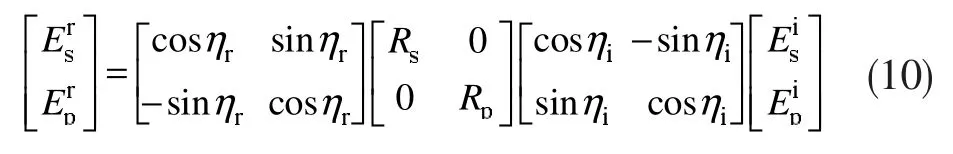
将菲涅耳反射率Rs、Rp带入式(10)可得：

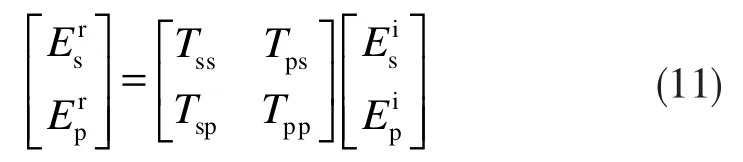
其中：

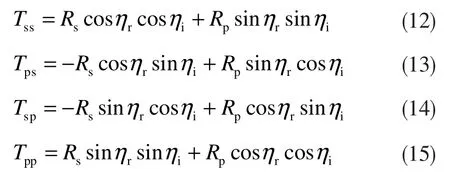
根据琼斯矩阵与穆勒矩阵M之间的转换关系[11]，M的各个分量Mij(i,j)=(0,1,2,3)可由琼斯矩阵分量推导得出，其中：

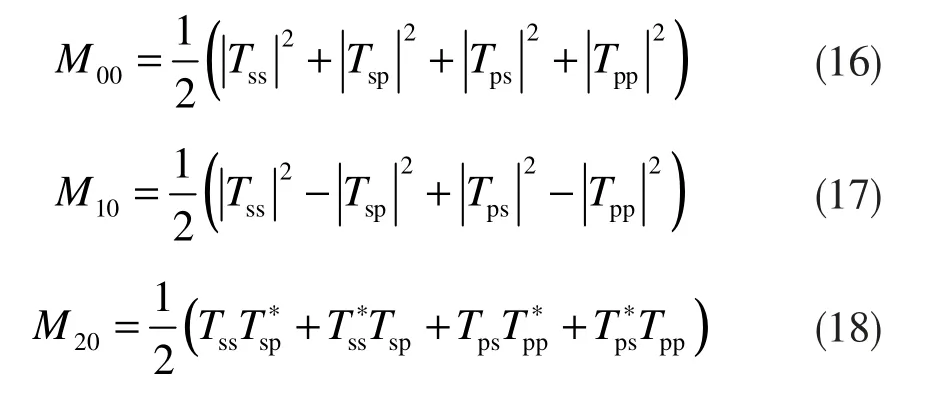
穆勒矩阵M(θi,θr,φi,φr)表示为：

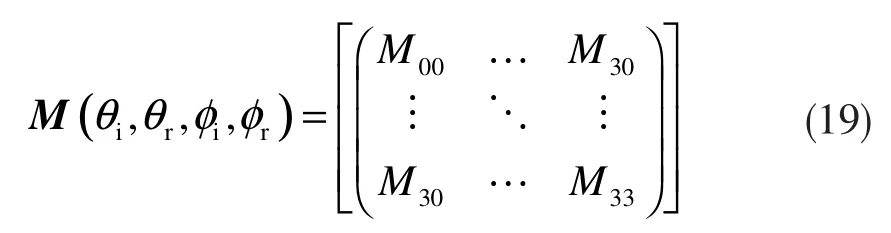
标量的BRDF模型与穆勒矩阵作用得到pBRDF模型：

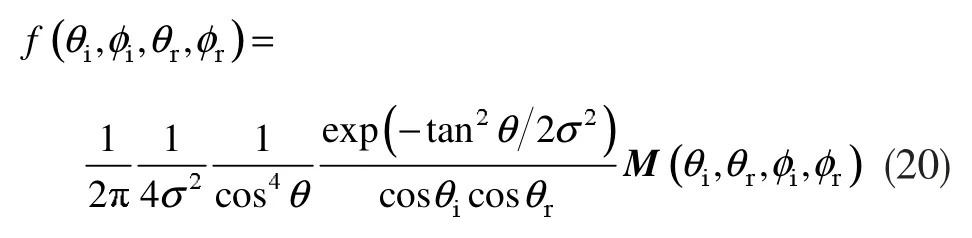
对pBRDF进行降维处理，忽略反射辐射中圆偏振分量，则F和M简化成3×3矩阵。

2.3 偏振度

入射非偏自然光的Stokes矢量在忽略椭圆偏振时为[1 0 0]，则反射的Stokes矢量Sr表示为：

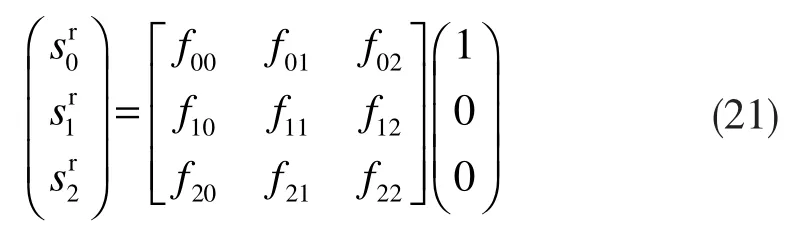
即为：

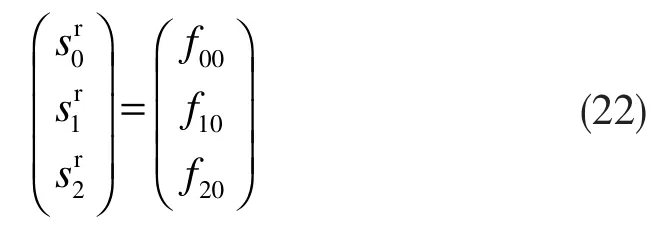
这里假设目标表面绝对光滑，粗糙度很小，从而忽略漫反射对偏振度的影响。偏振度定义为全偏振分量的强度与该光波的总强度之比，从而镜面反射Stokes 矢量的偏振度表达式为：

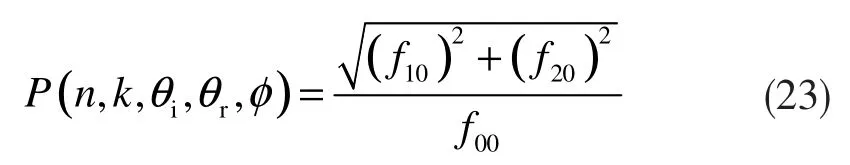
化简结果为：

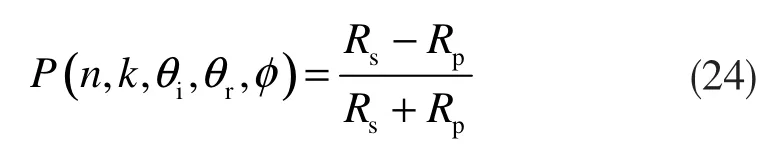
文献[9]通过实验证明了式(24)计算结果的准确性。以下以涂层[12]和金属表面为例对偏振度特性展开具体的仿真与分析。

3 仿真分析

仿真一：不同材料偏振度与入射角关系

选取四种材料：铜、铝、绿漆和黑漆，对其偏振度对入射角的关系进行仿真。四种材料的复折射率分别为：

铜：n=0.314，k=3.544

铝：n=1.24，k=6.6

绿漆：n=1.39，k=0.34

黑漆：n=1.405，k=0.2289

设置观测角θr=60°，方位角φ=φr-φi=180°。复折射率中n表示材料的折射率，决定光波在材料中的传播速度；k表示衰减系数，决定光在材料中的吸收特性。

金属是导体，对光波的吸收较大[13]，同时金属一般是非透明的，因此反射率也较大。而属于电介质材料的涂层绿漆和黑漆，它们的衰减系数k很小，而折射率n很高，根据布儒斯特定律，自然光以布儒斯特角入射到电介质材料表面时反射光是线偏振光[14-15]。因此，偏振度在布儒斯特角附近会出现极大值，而金属铜、铝的偏振度将随着入射角的增大而缓慢增大，这两种材料偏振度大小差别也较大。仿真得到的不同材料偏振度与入射角关系曲线如图3所示。

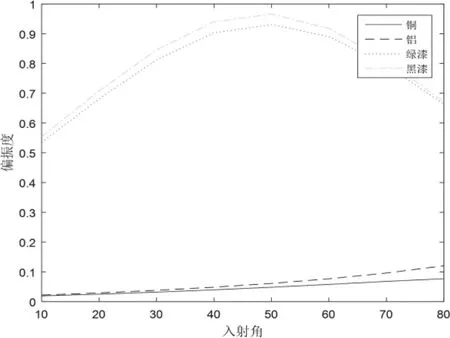
图3 不同材料偏振度与入射角关系

仿真二：偏振度与复折射率关系

仿真得到偏振度与复折射率关系如图4所示。任意材料在θr=60°，θi=60°，φ=180°下观测，从图中可看到偏振度分别随折射率n及吸收率k的变化规律。很明显偏振度随着折射率的增大而增大，随着吸收率的增大而减小。

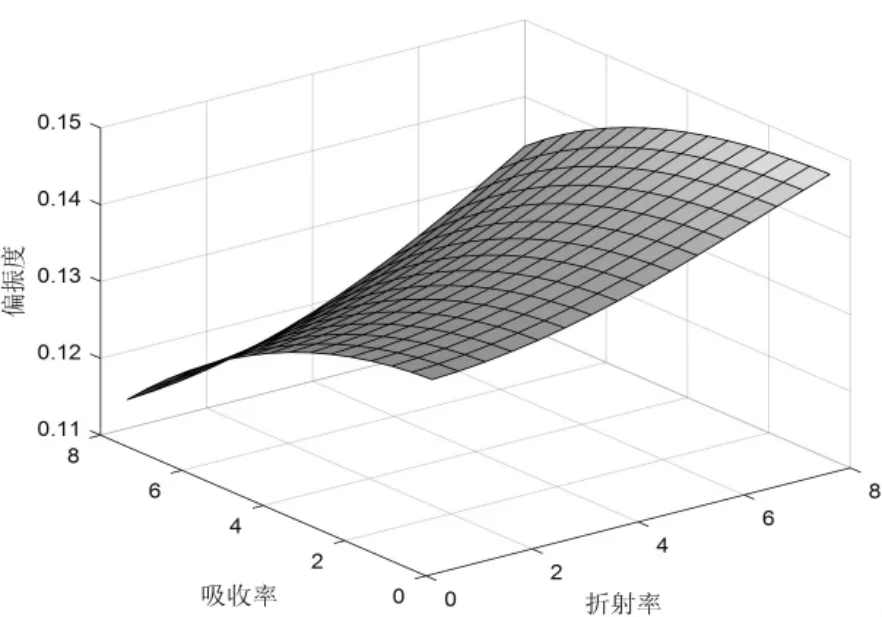
图4 偏振度与复折射率关系

仿真三：偏振度与方位角关系

仿真得到偏振度与方位角的关系如图5所示。可看出在绿漆材料θr=60°时，不同入射角条件下偏振度随方位角φ的变化。在入射角小于布儒斯特角时，随着入射角的增大偏振度增加，并且在φ=180°处取得偏振度的极大值；在大于布儒斯特角入射时，在φ=180°附近偏振度随着入射角的增大而减小，但是在其它方位角处偏振度反而在增大，结合图3综合得出电介质材料的偏振度在φ=180°±50°范围内随入射角增大而减小，在φ 为其它角度时偏振度随入射角的增大而增大。

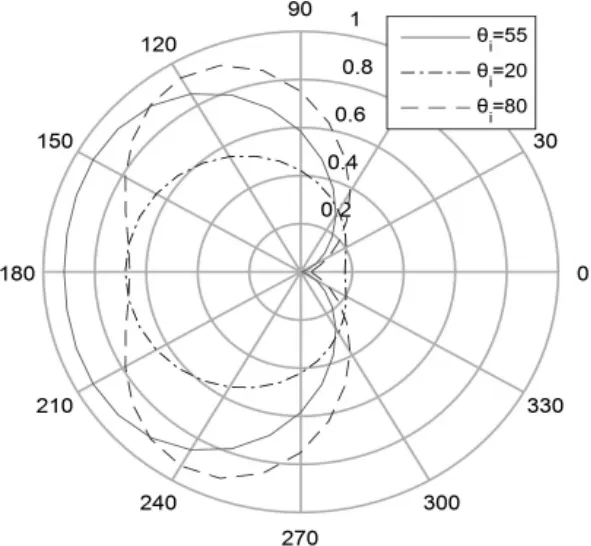
图5 偏振度与方位角关系

4 结 束 语

通过仿真四种材料单位面元在自然光入射条件下偏振度在不同条件下的变化，可分析得出材料的偏振度主要受材料复折射率、入射角及方位角的影响；电介质与导体的偏振度在同样观测条件下数值大小及变化规律都不相同，主要是由于材料复折射率的影响。基于这一偏振特性，偏振度可以应用于材料的分类和识别方面，尤其在空间目标的材料识别方面将更加具有实用意义。